Das Tau-Manifest
Michael Hartl Aus dem amerikanischen Englisch von Axel Scheithauer, Jonas Wagner und Johannes Clemens Huber
Tau-Tag, 2010Aktualisiert am Tau-Tag 2022
1 Die Kreiskonstante
Das Tau-Manifest ist einer der wichtigsten Zahlen der Mathematik gewidmet, vielleicht der wichtigsten: Der Kreiskonstanten, die den Umfang eines Kreises in Relation zu seiner linearen Dimension setzt. Seit Jahrtausenden gilt der Kreis als die vollkommenste aller Formen und die Kreiskonstante fasst die Geometrie des Kreises in einer einzigen Zahl zusammen. Natürlich ist die traditionelle Wahl für die Kreiskonstante \( \pi \) (pi)—aber, wie der Mathematiker Bob Palais es in seinem wunderbaren Artikel „\( \pi \) Is Wrong!“1 erklärt: \( \pi \) ist falsch. Es ist an der Zeit, die Angelegenheit zu bereinigen.
1.1 Ein unbescheidener Vorschlag
Wir beginnen damit, den von \( \pi \) angerichteten Schaden zu beheben, indem wir zunächst die berüchtigte Zahl selbst verstehen. Die traditionelle Definition der Kreiskonstante setzt \( \pi \) gleich dem Verhältnis von Umfang (Länge) und Durchmesser eines Kreises (Breite):2
Die Zahl \( \pi \) hat viele bemerkenswerte Eigenschaften—unter anderem ist sie irrational und sogar transzendent—und ihr Vorkommen in mathematischen Formeln ist weit verbreitet.
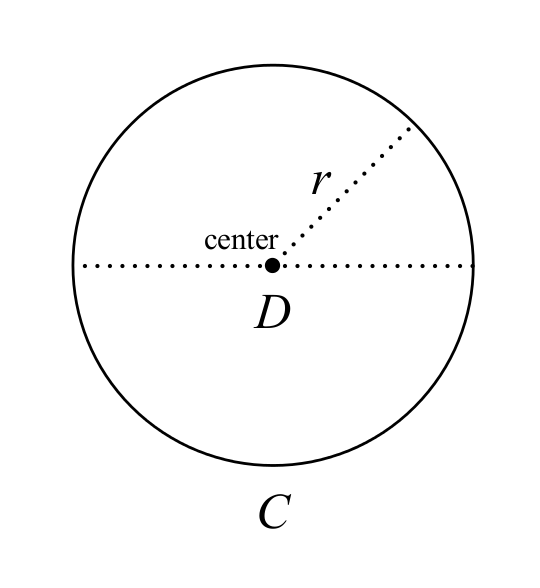
Es sollte offensichtlich sein, dass \( \pi \) nicht „falsch“ im Sinne von sachlich falsch ist; die Zahl \( \pi \) ist wohldefiniert und hat alle Eigenschaften, die ihr normalerweise von Mathematiker:innen zugeschrieben werden. Wenn wir sagen, dass „\( \pi \) falsch ist“, meinen wir, dass \( \pi \) eine verwirrende und unnatürliche Wahl für die Kreiskonstante ist. Insbesondere ist ein Kreis definiert als die Menge der Punkte mit einem festen Abstand, dem Radius, von einem gegebenen Punkt, dem Mittelpunkt (Abbildung 1). Während es unendlich viele Formen mit konstanter Breite gibt (Abbildung 2),3 gibt es nur eine Form mit konstantem Radius. Dies legt nahe, dass eine natürlichere Definition für die Kreiskonstante \( r \) anstelle von \( D \) verwenden könnte:
Da der Durchmesser eines Kreises das Doppelte seines Radius beträgt, ist diese Zahl numerisch gleich \( 2\pi \). Wie \( \pi \) ist sie transzendent und daher irrational, und (wie wir in Abschnitt 2 sehen werden) ihre Verwendung ist in der Mathematik ähnlich weit verbreitet.
In „\( \pi \) Is Wrong!“, argumentiert Bob Palais überzeugend zugunsten der zweiten dieser beiden Definitionen für die Kreiskonstante, und meines Erachtens gebührt ihm der Hauptverdienst, dieses Problem erkannt und einem breiten Publikum nahegebracht zu haben. Er nennt die wahre Kreiskonstante „eine Drehung (one turn)“, und er führt auch ein neues Symbol ein, um sie darzustellen (Abbildung 3). Wie wir sehen werden, ist die Beschreibung weitsichtig, aber leider ist das Symbol ziemlich seltsam, und (wie in Abschnitt 4 dargelegt) es scheint unwahrscheinlich, dass es sich durchsetzt. (Aktualisierung: Dies hat sich in der Tat bewahrheitet, und Palais selbst ist seitdem ein starker Befürworter der in diesem Manifest angeführten Argumente geworden.)

Das Tau-Manifest ist der These gewidmet, dass die richtige Reaktion auf „\( \pi \) ist falsch“ ist: „was du nicht sagst.“ Die wahre Kreiskonstante verdient einen eigenen Namen. Wie vielleicht schon zu erraten war, schlägt das Tau-Manifest vor, dass dieser Name der griechische Buchstabe \( \tau \) (tau) sein sollte:
Im weiteren Verlauf dieses Manifests werden wir sehen, dass die Zahl \( \tau \) die richtige Wahl ist, und wir werden durch die Nutzung (Abschnitt 2 and Abschnitt 3) und durch direkte Argumentation (Abschnitt 4) zeigen, dass auch der Buchstabe \( \tau \) eine natürliche Wahl ist.
1.2 Ein mächtiger Gegner
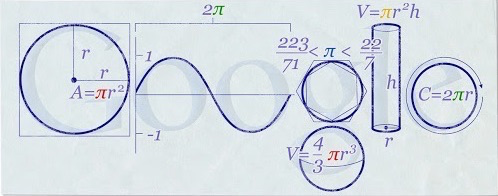
Bevor wir mit der Demonstration fortfahren, dass \( \tau \) die natürliche Wahl für die Kreiskonstante ist, wollen wir uns zunächst klar machen, womit wir es zu tun haben—denn es gibt eine mächtige, jahrhundertealte Verschwörung, die entschlossen ist, eine Pro-\( \pi \)-Propaganda zu verbreiten. Ganze Bücher werden geschrieben, um die Tugenden von \( \pi \) zu preisen. (Ich meine, Bücher!) Und die irrationale Verehrung für \( \pi \) hat sich sogar auf die höchsten Ebenen des Geekdoms ausgebreitet; zum Beispiel änderte Google am „Pi-Tag“ 2010 sein Logo, um \( \pi \) zu ehren (Abbildung 4).
In der Zwischenzeit lernen manche Menschen Dutzende, Hunderte oder sogar Tausende der Ziffern dieser mystischen Zahl. Was für ein trauriger Sack merkt sich bloß 40 Stellen von \( \pi \) (Abbildung 5)?4
Wahrlich, die Befürworter von \( \tau \) haben einen mächtigen Gegner. Und doch haben wir einen mächtigen Verbündeten—denn die Wahrheit ist auf unserer Seite.
2 Die Zahl Tau
Wir haben in Abschnitt 1.1 gesehen, dass die Zahl \( \tau \) auch als \( 2\pi \) geschrieben werden kann. Wie in „\( \pi \) Is Wrong!“ angemerkt, ist es daher von großem Interesse zu entdecken, dass die Kombination \( 2\pi \) mit erstaunlicher Häufigkeit in der Mathematik vorkommt. Betrachte zum Beispiel Integrale über den Raum in Polarkoordinaten:
Die obere Grenze der \( \theta \) Integration ist immer \( 2\pi \). Der gleiche Faktor tritt in der Definition der gaußschen (Normal) Verteilung auf,
und wieder in der Fourier-Transformation,
er taucht in der Cauchyschen Integralformel auf,
in der \( n \)-ten Einheitswurzel,
und in den Werten der Riemannschen Zeta-Funktion für positive gerade Ganzzahlen:5
Diese Formeln sind nicht handverlesen—schlage Dein Lieblingsbuch über Physik oder Mathematik auf und versuche es selbst. Es gibt noch unzählige weitere Beispiele, und die Schlussfolgerung ist eindeutig: \( 2\pi \) ist etwas Besonderes.
Um diesem Mysterium auf den Grund zu gehen, müssen wir zu den Grundbegriffen zurückkehren und die Natur von Kreisen und insbesondere die Natur von Winkeln betrachten. Obwohl vieles davon bekannt sein dürfte, lohnt es sich, es noch einmal durchzugehen, denn hier beginnt das wahre Verständnis von \( \tau \).
2.1 Kreise und Winkel
Zwischen Kreisen und Winkeln besteht eine enge Beziehung, wie in Abbildung 6 zu sehen ist. Da die konzentrischen Kreise in Abbildung 6 unterschiedliche Radien haben, schneiden die Geraden unterschiedliche Längen des Bogens ab, aber der Winkel \( \theta \) (theta) ist in allen Fällen gleich. Mit anderen Worten, die Größe des Winkels hängt nicht vom Radius des Kreises ab, der zur Definition des Bogens verwendet wird. Die grundlegende Aufgabe der Winkelmessung ist es, ein System zu schaffen, das diese Radiusinvarianz abbildet.

Das vielleicht bekannteste Winkelsystem ist Grad, welches einen Kreis in 360 gleiche Teile teilt. Ein Ergebnis dieses Systems ist die Menge der besonderen Winkel (Studierenden der Trigonometrie wohl bekannt) die in Abbildung 7 gezeigt werden.

Ein grundlegenderes System der Winkelmessung verwendet einen direkten Vergleich der Bogenlänge \( s \) mit dem Radius \( r \). Obwohl die Längen in Abbildung 6 unterschiedlich sind, wächst die Bogenlänge proportional zum Radius, so dass das Verhältnis der Bogenlänge zum Radius in jedem Fall dasselbe ist:
Dies legt die folgende Definition des Radianten nahe:
Diese Definition hat die geforderte Radiusinvarianz, und da sowohl \( s \) als auch \( r \) Längeneinheiten haben, ist Radiant eine Größe der Dimension Zahl. Die Angabe des Winkels in Radiant führt zu prägnanten und eleganten Formeln in der gesamten Mathematik; zum Beispiel ist die übliche Formel für die Ableitung von \( \sin\theta \) nur korrekt, wenn \( \theta \) in Radiant ausgedrückt wird:
Selbstverständlich können die besonderen Winkel in Abbildung 7 auch in Radianten ausgedrückt werden, und die besonderen Werte in Abbildung 8 sind wahrscheinlich noch aus dem Trigonometrie-Unterricht bekannt. (Ich nenne dieses Maßsystem „\( \pi \)-Radiant“ um zu betonen, dass es auf der Basis von \( \pi \) geschrieben ist.)


Bei kurzem Nachdenken fällt auf, dass die sogenannten „besonderen“ Winkel nur besonders einfache rationale Bruchteile eines Vollkreises sind, wie in Abbildung 9 veranschaulicht. Das legt nahe, Gleichung (4) nochmal zu betrachten, und die Bogenlänge \( s \) als Bruchteil \( f \) des vollen Umfangs \( C \) zu messen, d.h., \( s = f C \):
Beachte, wie natürlich \( \tau \) aus dieser Analyse hervorgeht. Das dadurch entstandene Diagramm der besonderen Winkel (Abbildung 10) wird, so fürchte ich, den Glauben der Gläubigen in seinen Grundfesten erschüttern.

Es gibt viele andere Argumente zu Gunsten von \( \tau \)—Abbildung 10 ist wohl das Bemerkenswerteste. In der Abbildung können wir auch das Genie von Bob Palais’ Identifikation der Kreiskonstanten als „ein Turn (Vollwinkel)“ erkennen: \( \tau \) ist der Radiant-Winkel für einen Turn eines Kreises. Besser noch, mit \( \tau \) muss man sich nichts merken: Ein Zwölftel eines Turns ist \( \tau/12 \), ein Achtel eines Turns ist \( \tau/8 \), und so weiter. Mit \( \tau \) bekommen wir das Beste zweier Welten durch die Kombination konzeptueller Klarheit mit all den konkreten Vorteilen von Radiant; die abstrakte Bedeutung von, sagen wir, \( \tau/12 \) is offensichtlich, aber sie ist ebenso nur eine Zahl:
Und schließlich, durch Vergleichen der beiden Abbildungen 8 und 10, können wir sehen, woher diese lästigen Faktoren von \( 2\pi \) kommen: Eine Umdrehung eines Kreises ist \( 1\tau \), aber \( 2\pi \). Numerisch sind sie gleich, aber konzeptionell sind sie sehr verschieden.
Die Konsequenzen
Die überflüssigen Faktoren von \( 2 \), die durch die Verwendung von \( \pi \) auftreten, sind für sich genommen schon lästig genug, noch viel schädlicher ist jedoch ihre Tendenz, sich aufzuheben, wenn sie durch eine gerade Zahl geteilt werden. Die absurden Ergebnisse, etwa dass \( \pi \) halbe für eine Viertelumdrehung steht, verschleiern die zugrundeliegende Beziehung zwischen Winkelmessung und der Kreiskonstante. Diejenigen, die sagen, dass es doch „egal“ sei, ob wir \( \pi \) oder \( \tau \) in der Trigonometriestunde verwenden, möchte ich einfach mal bitten, Abbildung 8, Abbildung 9, und Abbildung 10 durch die Augen eines Schulkindes zu betrachten. Es ist leicht zu erkennen, dass aus der Perspektive eines Anfängers die Verwendung von \( \pi \) anstelle von \( \tau \) eine pädagogische Katastrophe ist.
2.2 Die Kreisfunktionen
Auch wenn die Winkelmessung in Radiant einige der überzeugendsten Argumente für die wahre Kreiskonstante liefert, lohnt es sich, die Vorzüge von \( \pi \) und \( \tau \) in einigen anderen Zusammenhängen zu betrachten. Wir beginnen mit den wichtigen grundlegenden Funktionen \( \sin\theta \) und \( \cos\theta \). Auch bekannt als die „Kreisfunktionen“, da sie die Koordinaten eines Punkts auf dem Einheitskreis (ein Kreis mit dem Radius \( 1 \)) angeben, sind Sinus und Cosinus die fundamentalen Funktionen der Trigonometrie (Abbildung 11).

Untersuchen wir die Graphen der Kreisfunktion, um ihr Verhalten besser zu verstehen.6 In Abbildung 12 und Abbildung 13 ist gut zu erkennen, dass beide Funktionen periodisch sind mit Periode \( T \). Wie in Abbildung 12 gezeigt, startet die Sinusfunktion \( \sin\theta \) bei Null, erreicht ein Maximum bei einer Viertelperiode, geht durch Null bei der halben Periode, erreicht ein Minimum bei drei Vierteln einer Periode, und kehrt zu Null zurück nach einer ganzen Periode. Gleichzeitig startet die Cosinusfunktion \( \cos\theta \) mit einem Maximum, hat ein Minimum bei einer halben Periode, und geht durch Null bei einem Viertel und drei Vierteln einer Periode (Abbildung 13). Zum Vergleich zeigen beide Abbildungen den Wert von \( \theta \) (in Radiant) an jedem besonderen Punkt.


Da Sinus und Cosinus für jede volle Drehung des Kreises durch einen vollen Zyklus gehen, gilt natürlich \( T = \tau \); d.h., die Periode der Kreisfunktionen ist gleich der Kreiskonstanten. Infolgedessen sind die „besonderen“ Werte von \( \theta \) völlig natürlich: Eine Viertelperiode ist \( \tau/4 \), eine halbe Periode ist \( \tau/2 \), usw. Tatsächlich, als ich die Abbildung 12 erstellte, fragte ich mich einmal, was der numerische Wert von \( \theta \) für den Nulldurchgang der Sinusfunktion sei. Da der Nulldurchgang bei der Hälfte der Periode stattfindet und da \( \tau \approx 6.28 \), ergab eine Überschlagsrechnung folgendes Ergebnis:
Ganz recht: Ich war überrascht zu entdecken, dass ich schon vergessen hatte, dass \( \tau/2 \) manchmal „\( \pi \)“ genannt wird. Vielleicht ist Dir das auch gerade passiert. Willkommen in meiner Welt.
2.3 Die Eulersche Identität
Es wäre unverzeihlich, in diesem Manifest nicht die Eulersche Identität zu erwähnen, manchmal als die „schönste Gleichung der Mathematik“ bezeichnet. Diese Identität enthält eine komplexe Potenzierung, die eine enge Verbindung zur Kreisfunktion und auch zur Geometrie des Kreises an sich hat.
Je nach gewählter Route kann die folgende Gleichung entweder als Theorem bewiesen oder als Definition vorrausgesetzt werden; in jedem Fall ist sie sehr bemerkenswert:
Als Eulers Formel (nach Leonhard Euler) bekannt, verbindet diese Gleichung eine Potenzierung mit imaginären Argument mit den Kreisfunktionen Sinus und Cosinus und der imaginären Einheit \( i \). Die Rechtfertigung der Eulerschen Formel sprengt natürlich den Rahmen dieses Manifests, doch ihre Herkunft ist über jeden Verdacht erhaben, und ihre Bedeutung unstrittig.
Wertet man Gleichung (6) bei \( \theta = \tau \) aus, erhält man
was sich vereinfachen lässt zur Eulerschen Identität:7
In Worten ausgedrückt, macht die Gleichung (8) folgende fundamentale Beobachtung:
Die Exponentialfunktion des Produkts der imaginären Einheit mit der Kreiskonstanten ist die Einheit.
Geometrisch korrespondiert die Multiplikation mit \( e^{i\theta} \) mit der Rotation einer komplexen Zahl um den Winkel \( \theta \) in der komplexen Ebene, was wiederum eine zweite Interpretation der Eulerschen Identität nahelegt:
Die Rotation um eine Drehung ist 1.
Die Zahl \( 1 \) ist das neutrale Element der Multiplikation. Daher ist die geometrische Bedeutung von \( e^{i\tau} = 1 \), dass die Rotation eines Punktes der komplexen Ebene um eine volle Umdrehung ihn einfach an seine ursprüngliche Position zurückführt.
Wie im Fall der Winkelmessung in Radiant sehen wir, wie natürlich die Verbindung zwischen \( \tau \) und einer Umdrehung eines Kreis ist. Tatsächlich: Wenn man \( \tau \) mit „einer Umdrehung“ identifiziert, klingt die Eulersche Identität fast wie eine Tautologie.
Nicht die schönste Gleichung
Natürlich verwendet die traditionelle Form der Eulerschen Identität \( \pi \) an Stelle von \( \tau \). Um sie abzuleiten, starten wir mit der Berechnung von Eulers Formel bei \( \theta = \pi \). Dies ergibt
und wird vereinfacht zu
Nur ist dieses Minuszeichen so häßlich, dass die Gleichung (10) fast immer sofort umgeformt wird, um die folgende „schöne“ Gleichung zu bekommen:
An dieser Stelle klärt uns der Kommentator üblicherweise mit grandioser Geste darüber auf, dass die Gleichung (11) \( 0 \), \( 1 \), \( i \), \( e \), and \( \pi \) verknüpft—manchmal die „fünf wichtigsten Zahlen der Mathematik“ genannt.
In diesem Zusammenhang ist es bemerkenswert, wie viele Leute beklagen, dass Gleichung (8) nur vier dieser fünf Zahlen enthält. Also gut:
Tatsächlich war in Gleichung (7) bereits ein \( 0i \) enthalten (von \( i \sin \tau \)):
Gleichung (13), ohne Umformung, setzt tatsächlich die fünf wichtigsten Zahlen der Mathematik in Beziehung zueinander: \( 0 \), \( 1 \), \( i \), \( e \), und \( \tau \).
Eulersche Identitäten
Da man Null in jeder Gleichung irgendwo dazuaddieren kann, ist die Einführung der \( 0 \) in Gleichung (12) ein etwas augenzwinkernder Kontrapunkt zu \( e^{i\pi} + 1 = 0 \). Die Identität \( e^{i\pi} = -1 \) ermöglicht jedoch auch noch eine ernstzunehmendere Einsicht. Schauen wir mal, was passiert, wenn wir sie mit \( \tau \) ausdrücken:
Geometrisch sagt uns das, dass eine Rotation um eine halbe Drehung dasselbe ist, wie die Multiplikation mit \( -1 \). Und genau so ist es: Nach einer Drehung um \( \tau/2 \) Radiant wird die komplexe Zahl \( z = a + ib \) auf \( -a - ib \) abgebildet, was tatsächlich einfach \( -1\cdot z \) ist.
Schreibt man die Eulersche Identität mit \( \tau \), können wir sehen, dass die „originale“ Form der Eulerschen Identität (Gleichung (10)) eine transparente geometrische Bedeutung hat, die ihr fehlt, wenn man sie mit \( \pi \) schreibt. (Natürlich kann \( e^{i\pi} = -1 \) als Rotation um \( \pi \) Radiant verstanden werden, nur zeigt die nahezu allgegenwärtige Umformung zu \( e^{i\pi} + 1 = 0 \), wie die Verwendung von \( \pi \) von der natürlichen geometrischen Bedeutung der Identität ablenkt.) Die Viertelkreis-Identäten haben gleichartige geometrische Interpretationen: Gleichung (6) bei \( \tau/4 \) ausgewertet ergibt \( e^{i\tau/4} = i \), was nichts anderes aussagt, als dass eine Viertelumdrehung in der komplexen Ebene dasselbe ist wie eine Multiplikation mit \( i \); auf gleiche Weise sagt \( e^{i\cdot(3\tau/4)} = -i \), dass eine Dreivierteldrehung dasselbe ist wie eine Multiplikation mit \( -i \). Die Zusammenfassung dieser Ergebnisse wollen wir Eulersche Identitäten nennen. Sie erscheint in Tabelle 1.
| Rotationswinkel | Eulersche Identität | ||
| \( 0 \) | \( e^{i\cdot0} \) | \( = \) | \( 1 \) |
| \( \tau/4 \) | \( e^{i\tau/4} \) | \( = \) | \( i \) |
| \( \tau/2 \) | \( e^{i\tau/2} \) | \( = \) | \( -1 \) |
| \( 3\tau/4 \) | \( e^{i\cdot(3\tau/4)} \) | \( = \) | \( -i \) |
| \( \tau \) | \( e^{i\tau} \) | \( = \) | \( 1 \) |
Diese Analyse können wir noch einen Schritt weiter führen, indem wir bemerken, dass für jeden Winkel \( \theta \), \( e^{i\theta} \) als Punkt interpretiert werden kann, der auf dem Einheitskreis in der komplexen Ebene liegt. Da die komplexe Ebene die horizontale Achse mit dem Realteil und die vertikale Achse mit dem Imaginärteil identifiziert, sagt uns Eulers Formel, dass \( e^{i\theta} \) mit den Koordinaten \( (\cos\theta, \sin\theta) \) korrespondiert. Setzen wir die Werte der „besonderen“ Winkel aus Abbildung 10 in Gleichung (6) ein, ergeben sie die Punkte in Tabelle 2, und Auftragen dieser Punkte in der komplexen Ebene ergibt Abbildung 14. Ein Vergleich der Abbildung 14 mit Abbildung 10 zerstreut schnell alle Zweifel, welche Wahl der Kreiskonstanten die Beziehung zwischen Eulers Formel und der Geometrie des Kreises besser aufzeigt.
| Polarform | Rechtwinklige Form | Koordinaten |
| \( e^{i\theta} \) | \( \cos\theta + i\sin\theta \) | \( (\cos\theta, \sin\theta) \) |
| \( e^{i\cdot0} \) | \( 1 \) | \( (1, 0) \) |
| \( e^{i\tau/12} \) | \( \frac{\sqrt{3}}{2} + \frac{1}{2}i \) | \( (\frac{\sqrt{3}}{2}, \frac{1}{2}) \) |
| \( e^{i\tau/8} \) | \( \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i \) | \( (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) \) |
| \( e^{i\tau/6} \) | \( \frac{1}{2} +\frac{\sqrt{3}}{2} i \) | \( (\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( e^{i\tau/4} \) | \( i \) | \( (0, 1) \) |
| \( e^{i\tau/3} \) | \( -\frac{1}{2} +\frac{\sqrt{3}}{2} i \) | \( (-\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( e^{i\tau/2} \) | \( -1 \) | \( (-1, 0) \) |
| \( e^{i\cdot(3\tau/4)} \) | \( -i \) | \( (0, -1) \) |
| \( e^{i\tau} \) | \( 1 \) | \( (1, 0) \) |

3 Kreisfläche: Der Gnadenstoß
Wenn Du als \( \pi \)-Gläubige:r bis hierhin gekommen sind, dürftest Du nun wirklich angefangen haben, Deinen Glauben zu hinterfragen. \( \tau \) ist so natürlich, seine Bedeutung so transparent—gibt’s denn kein Beispiel, in dem \( \pi \) leuchtet in all seiner Pracht? Eine schemenhafte Erinnerung regt sich—ja, da gibt es eine Formel—es ist die Formel für die Kreisfläche! Erschauet:
Nein, warte. Die Flächenformel wird immer mit dem Radius geschrieben, wie folgt:
Hier sehen wir \( \pi \), ungeschminkt, in einer der wichtigsten Gleichungen der Mathematik—eine Formel, schon von Archimedes höchstselbst bewiesen. Die Ordnung ist wieder hergestellt! Und doch, der Name des Abschnitts klingt unheilvoll… Wenn diese Gleichung \( \pi \)’s Krönung ist, wie kann sie gleichzeitig ihr Gnadenstoß sein?
3.1 Quadratische Formen
Untersuchen wir dieses vermeintliche Musterbeispiel von \( \pi \), \( A = \pi r^2 \). Es fällt auf, dass der Radius zum Quadrat darin vorkommt. Das macht die Formel zu einer einfachen quadratischen Form. Solche Formen ergeben sich in vielen Zusammenhängen; als Physiker sind meine Lieblingsbeispiele aus dem Lehrplan der Grundlagen der Physik. Betrachten wir einige der Reihe nach.
Fallen in einem einheitlichen Gravitationsfeld
Galileo Galilei hat herausgefunden, dass die Geschwindigkeit einen Objekts, das in einem einheitlichen Gravitationsfeld fällt, proportional zur Zeit ist, die es gefallen ist:
Die Proportionalitätskonstante ist die Gravitationsbeschleunigung \( g \):
Da die Geschwindigkeit die Ableitung der Position ist, können wir die gefallene Distanz durch Integration berechnen:8
Potentielle Energie einer linearen Feder
Robert Hooke hat herausgefunden, dass die externe Kraft, die gebraucht wird, um eine Feder zu spannen, proportional zur Auslenkung der Feder aus der Ruhelage ist:
Die Proportionalitätskonstante ist die Federkonstante \( k \):9
Die potentielle Energie in der Feder ist dann gleich der Arbeit, die durch die externe Kraft geleistet wurde:
Bewegungsenergie
Isaac Newton hat herausgefunden, dass die Kraft auf ein Objekt proportional zu seiner Beschleunigung ist:
Die Proportionalitätskonstante ist die Masse \( m \):
Die Bewegungsenergie, oder kinetische Energie, ist gleich der Arbeit, die benötigt wurde, um die Masse auf ihre Geschwindigkeit \( v \) zu beschleunigen:
3.2 Ein Gefühl der Vorahnung
Nachdem Du einige Beispiele einfacher quadratischer Formen aus der Physik gesehen hast, könntest Du eine böse Vorahnung haben, wohin die Reise geht, wenn wir nun zur Geometrie des Kreises zurückkehren. Dieses Gefühl ist gerechtfertigt.

Wie in Abbildung 15 gezeigt, kann die Fläche eines Kreises berechnet werden, indem man ihn in Ringe der Länge \( C \) und Breite \( dr \) zerlegt. Die Fläche jedes Rings ist \( C\,dr \):
Nun ist ja der Umfang eines Kreises proportional zu seinem Radius:
Die Proportionalitätskonstante ist \( \tau \):
Die Fläche des Kreises ist das Integral über alle seine Ringe:
Solltest Du am Anfang dieses Abschnitts immer noch ein:e \( \pi \)-Partisan:in gewesen sein, ist Dein Kopf nun explodiert. Denn selbst in diesem Fall, in dem \( \pi \) angeblich glänzt, fehlt in Wirklichkeit ein Faktor von \( 2 \). Tatsächlich zeigt auch der originale Beweis von Archimedes mitnichten, dass die Kreisfläche \( \pi r^2 \) ist, sondern dass sie gleich der Fläche eines rechtwinkligen Dreiecks mit der Grundlinie \( C \) und Höhe \( r \) ist. Wendet man darauf die Formel für die Fläche eines Dreiecks an, dann ergibt sich
Man kommt einfach nicht um den Faktor \( \frac{1}{2} \) herum (Tabelle 3).
| Größe | Symbol | Formel |
| gefallene Distanz | \( y \) | \( \textstyle{\frac{1}{2}}gt^2 \) |
| Federenergie | \( U \) | \( \textstyle{\frac{1}{2}}kx^2 \) |
| Kinetische Energie | \( K \) | \( \textstyle{\frac{1}{2}}mv^2 \) |
| Kreisfläche | \( A \) | \( \textstyle{\frac{1}{2}}\tau r^2 \) |
Quod erat demonstrandum
Wir wollten in diesem Manifest zeigen, dass \( \tau \) die wahre Kreiskonstante ist. Da die Formel für die Kreisfläche so ziemlich das letzte und beste Argument für \( \pi \) war, lehne ich mich an dieser Stelle mal weit aus dem Fenster und sage: Q.E.D.
4 Konflikt und Widerstand
Trotz der definitiven Demonstration seiner Überlegenheit gibt es immer noch viele, die gegen \( \tau \) sind, sowohl als Notation als auch als Zahl. In diesem Abschnitt kümmern wir uns um die Bedenken derjenigen, die den Wert akzeptieren, aber nicht den Buchstaben. Wir widerlegen dann einige der vielen Argumente, die gegen \( C/r \) selbst vorgebracht werden, inklusive des sogenannten „Pi-Manifests“, welches das Primat von \( \pi \) verteidigt. In diesem Zusammenhang werden wir das recht fortgeschrittene Thema des Volumens einer Hypersphäre erörtern (Abschnitt 5.1), welches die Argumente in Abschnitt 3 zur Kreisfläche ergänzt und erweitert.
4.1 Eine Drehung
Der Prüfstein für jede Notation ist ihre Verwendung; da Du \( \tau \) bereits überall im vorliegenden Manifest im Einsatz gesehen hast, bist Du womöglich schon davon überzeugt, dass es seine Aufgabe gut erfüllt. Aber bei einer so fundamentalen Konstante wie \( \tau \) sollten wir einen tieferen Grund für unsere Wahl haben. Warum nicht \( \alpha \), zum Beispiel, oder \( \omega \)? Was macht \( \tau \) so großartig?
Es gibt zwei Hauptgründe für die Verwendung von \( \tau \) für die Kreiskonstante. Der erste ist, dass \( \tau \) graphisch \( \pi \) ähnelt: Nach Jahrhunderten der Verwendung ist die Verbindung von \( \pi \) mit der Kreiskonstanten unvermeidlich, und mit der Wahl von \( \tau \) profitieren wir von der Assoziation, statt sie zu bekämpfen. (Tatsächlich könnte die horizontale Linie in jedem Buchstaben nahelegen, dass wir die „Beine“ als Nenner interpretieren, so dass \( \pi \) zwei Beine im Nenner hat, während \( \tau \) nur eines hat. Wenn man das so betrachtet, ist die Beziehung \( \tau = 2\pi \) ganz natürlich.)10
Der zweite Grund ist, dass \( \tau \) einer Drehung in einem Kreis entspricht. Vielleicht ist Dir aufgefallen, dass „\( \tau \)“ und „turn“ (Englisch für Drehung) beide mit einem „t“-Laut starten. Das war auch die ursprüngliche Motivation für die Wahl von \( \tau \), und sie ist kein Zufall: Die Herkunft des englischen Worts „turn“ ist das griechische τόρνος (tornos), das „Drehbank“ bedeutet. Benutzen wir einen Mathematik-Font für den ersten Buchstaben in τόρνος erhalten wir: \( \tau \).
Seit der ersten Veröffentlichung des Tau-Manifests habe ich erfahren, dass Peter Harremoës 2010 unabhängig dem „\( \pi \) Is Wrong!“ Autor Bob Palais vorgeschlagen hatte, \( \tau \) zu verwenden; John Fisher schlug \( \tau \) 2004 in einem Usenet post vor, und Joseph Lindenberg hat sowohl das Argument als auch das Symbol mehr als zwanzig Jahre früher vorweggenommen!11 Dr. Harremoës insbesondere hat die Bedeutung eines Punkts hervorgehoben, der zuerst in Abschnitt 1.1 gemacht wurde: Die Verwendung von \( \tau \) gibt der Kreiskonstante einen Namen. Da \( \tau \) ein normaler griechischer Buchstabe ist, können Leute, die ihn zum ersten Mal sehen, ihn sofort aussprechen. Außerdem funktioniert \( \tau \), anders als die Bezeichnung der Kreiskonstante als „Drehung“, sowohl im schriftlichen als auch im mündlichen Kontext gut. Zum Beispiel, zu sagen, dass ein Viertelkreis ein Radiant Winkelmaß von „einer ViertelDrehung“ hat, klingt großartig, aber „Drehung durch vier Radianten“ klingt unbeholfen, und „die Fläche eines Kreises ist eine halbe Drehung \( r \) Quadrat“ klingt ausgesprochen seltsam. Mit \( \tau \) können wir sagen, „Tau durch vier Radianten“ und „die Fläche eines Kreises ist ein halbes Tau \( r \) Quadrat.“
Zweideutige Notation
Natürlich besteht bei jeder neuen Notation die Möglichkeit eines Konflikts mit dem derzeitigen Sprachgebrauch. Wie in Abschnitt 1.1 ausgeführt, vermeidet „\( \pi \) Is Wrong!“ das Problem durch die Einführung eines neuen Symbols (Abbildung 3). Hierfür gibt es Präzedenzfälle; zum Beispiel wurde von Max Planck in den frühen Tagen der Quantenmechanik die Konstante \( h \) eingeführt, die die Energie eines Lichtteilchens in Relation zu seiner Frequenz setzt (durch \( E = h\nu \)), aber Physiker erkannten bald, dass es oft bequemer ist \( \hbar \) (lies „h-quer“) zu verwenden—wobei \( \hbar \) einfach \( h \) geteilt durch… ähem… \( 2\pi \) ist—und diese Verwendung ist nun Standard.
Aber Akzeptanz für ein neues Symbol zu erreichen ist schwierig: man muss ihm einen Namen geben, der Name muss bekannt gemacht werden und das Symbol selbst muss Textverarbeitungs- und Schriftsatzsystemen hinzugefügt werden. Zudem würde die Festlegung eines neuen Symbols für \( 2\pi \) die Kooperation der akademischen mathematischen Gemeinschaft erfordern, die zum Thema \( \pi \) vs. \( \tau \) bisher bestenfalls apathisch und schlimmstenfalls feindselig war.12 Die Verwendung eines bestehenden Symbols ermöglicht es uns, das mathematische Establishment zu umgehen.13
Statt für ein neues Symbol einzutreten, optiert das Tau-Manifest für einen bestehenden griechischen Buchstaben. Daher müssen wir, da \( \tau \) schon in anderen aktuellen Kontexten verwendet wird, die Konflikte mit bestehender Praxis behandeln. Glücklicherweise gibt es erstaunlich wenige gebräuchliche Verwendungen. Außerdem wird \( \tau \) zwar für einige spezifische Variablen verwendet—z.B. Scherbelastung im Maschinenbau, Drehmoment in der Rotationsmechanik und Eigenzeit in der speziellen und allgemeinen Relativitätstheorie—aber es gibt keine universelle widersprüchliche Verwendung.14 In diesen Fällen können wir entweder die Mehrdeutigkeit tolerieren oder die wenigen vorhandenen Konflikte umgehen, indem wir die Notation selektiv ändern, z.B. \( N \) für das Drehmoment verwenden15, \( \tau_p \) für Eigenzeit, oder sogar \( \tau_\odot \) oder \( \uptau \) für die Kreiskonstante selbst.
Ungeachtet dieser Argumente haben potentielle Benutzungskonflikte sich als größte Quelle des Widerstands gegen \( \tau \) herausgestellt. Einige Korrespondenten haben sogar rundheraus bestritten, dass \( \tau \) (oder vermutlich jegliches andere derzeit verwendete Symbol) diese Probleme überwinden könnte. Wissenschaftler und Ingenieure haben jedoch eine hohe Toleranz gegenüber mehrdeutigen Bezeichnungen. Zu behaupten, \( \tau \)-die-Kreiskonstante könne nicht mit anderen Verwendungen koexistieren, ignoriert substanzielle Beweise für das Gegenteil.
Eine dieser leicht zu tolerierenden Mehrdeutigkeiten findet sich in der Quantenmechanik, wo wir folgende Formel für den Bohrschen Radius finden. Dies ist, grob gesagt, die „Größe“ eines Wasserstoffatoms in seinem niedrigsten Energiezustand (dem Grundzustand):
mit \( m \) gleich der Elektronenmasse und \( e \) seiner Ladung. Der Grundzustand wird durch eine sogenannte Wellenfunktion beschrieben, welche exponentiell mit steigendem Radius abfällt, wobei die Größenordnung durch den Bohrschen Radius bestimmt wird:
mit \( N \) als normalisierender Konstante.
Hast du das Problem bereits entdeckt? Möglicherweise nicht, was ja auch gerade der Punkt ist. Das „Problem“ ist, dass \( e \) in Gleichung (14) und \( e \) in Gleichung (15) nicht dasselbe \( e \) sind—das erste bezeichnet die Elektronenladung, und das zweite ist die Eulersche Zahl (die Basis des natürlichen Logarithmus). Tatsächlich, wenn wir den Faktor \( a_0 \) im Exponenten der Gleichung (15) erweitern, erhalten wir
worin \( e \) hoch irgendwas mit \( e \) vorkommt. Es kommt sogar noch schlimmer, denn \( N \) selbst enthält ebenfalls ein \( e \):
Ich habe keinen Zweifel daran, dass—würde eine Notation für die Eulersche Zahl nicht bereits existieren—jeder Vorschlag von \( e \) mit dem Argument abgeschmettert würde, dass es Konflikte mit anderen Verwendungen gibt. Nichtsdestotrotz hat in der Praxis niemand je ein Problem damit, \( e \) in beiden Kontexten zu verwenden. Es gibt noch viele weitere Beispiel, einschließend solcher, wo \( \pi \) für zwei unterschiedliche Dinge verwendet wird.16 Es ist schwer einzusehen, dass die Verwendung von \( \tau \) für unterschiedliche Größen anders sein soll.
Nebenan bemerkt, werden die \( \pi \)-Pedant:innen (von denen es nicht wenige gibt) möglicherweise anmerken, dass die Wellenfunktion des Grundzustandes des Wasserstoffatoms einen Faktor \( \pi \) enthält:
Auf den ersten Blick erscheint dies natürlicher als die Version mit \( \tau \):
Wie üblich trügt der Schein: der Wert von \( N \) kommt von dem Produkt
was aufzeigt, dass die Kreiskonstante über einen Faktor \( 1/\sqrt{2\pi} \), d.h., \( 1/\sqrt{\tau} \), in diese Gleichung eintritt. Genau wie bei der Formel für die Kreisfläche ist es also bloß Zufall, dass \( \pi \) alleine übrig bleibt.
4.2 Das Pi-Manifest
Obwohl die meisten Einwände gegen \( \tau \) aus verstreuter Email-Korrespondenz und diversen Kommentaren im Netz stammen, gibt es auch einen organisierten Widerstand. Insbesondere seit der Veröffentlichung des Tau-Manifests im Juni 2010 ist ein „Pi-Manifest“ aufgetaucht, um für die traditionelle Kreiskonstante zu plädieren. Dieser Abschnitt und die beiden folgenden enthalten eine Widerlegung seiner Argumente.17 Diese Behandlung ist zwangsweise knapper formuliert und fachlich weiter fortgeschritten als der Rest des Manifests, aber selbst ein oberflächliches Lesen von dem, was folgt, wird eine Vorstellung von der Schwäche des Pi-Manifests geben.
Während wir das Erscheinen des Pi-Manifests sicherlich als gutes Zeichen für anhaltendes Interesse an diesem Thema sehen können, werden darin mehrere falsche Behauptungen aufgestellt. Zum Beispiel, dass der Faktor \( 2\pi \) in der Gaußschen (Normal-)Verteilung ein Zufall ist und naturgemäßer geschrieben werden kann als
Das ist falsch: Der Faktor \( 2\pi \) stammt von der Quadratur der nicht normalisierten Gauß-Verteilung und dem Wechsel zu Polarkoordinaten, welche zu einem Faktor \( 1 \) des radialen Integrals und einem \( 2\pi \) des angularen Integrals führt. So wie im Fall einer kreisförmigen Fläche, stammt der Faktor \( \pi \) von \( 1/2\times 2\pi \), und nicht von \( \pi \) alleine.
Eine verwandte Behauptung ist, dass der Wert der Gammafunktion an der Stelle \( 1/2 \) naturgemäßer in Form von \( \pi \) sei:
mit
Aber \( \Gamma(\frac{1}{2}) \) reduziert sich auf dasselbe Gauß-Integral, wie in der Normalverteilung (indem wir \( u = x^{1/2} \) setzen), also ist \( \pi \) iin diesem Fall ebenfalls eigentlich \( 1/2\times 2\pi \). Tatsächlich gelangt die Kreiskonstante, wie in vielen Fällen im Pi-Manifest angeführt, durch ein Integral über alle Winkel hinein, und zwar indem \( \theta \) sich von \( 0 \) bis \( \tau \) erstreckt.
Das Pi-Manifest untersucht auch ein paar Formeln für regelmäßige \( n \)-seitige Polygone (oder „\( n \)-Ecke“). Es merkt beispielsweise an, dass die Summe der Innenwinkel eines \( n \)-Ecks wie folgt entsteht:
Dieses Problem wurde in „\( \pi \) Is Wrong!“ adressiert, wo Folgendes angemerkt wird: „Die Summe der Innenwinkel [eines Dreiecks] ist \( \pi \), zugegeben. Aber die Summe der Außenwinkel jedes Polygons, von der mühelos die Innenwinkelsumme abgeleitet werden kann, und welche sich auf das Integral der Krümmung einer einfachen geschlossenen Kurve verallgemeinern lässt, ist \( 2\pi \).“ Zusätzlich dazu bietet das Pi-Manifest die Formel für den Flächeninhalt eines \( n \)-Ecks mit Einheitsradius (der Abstand von Mittelpunkt zu Eckpunkt),
und nennt sie „zweifelsohne… einen weiteren Sieg für \( \pi \).“ Aber die Verwendung der Doppelwinkel-Identität \( \sin\theta\cos\theta = \frac{1}{2} \sin 2\theta \) zeigt, dass diese als
geschrieben werden kann, was nichts anderes ist als
In anderen Worten hat die Fläche eines \( n \)-Ecks einen natürlichen Faktor \( 1/2 \). Tatsächlich liefert die Grenzwertbildung von Eq. (17) mit \( n\rightarrow \infty \) (und Verwendung der Regel von L’Hôpital) die Fläche eines regelmäßigen Einheitspolygons mit unendlich vielen Seiten, sprich einen Einheitskreis:
In diesem Zusammenhang sollten wir anmerken, dass das Pi-Manifest viel Aufhebens darum macht, dass \( \pi \) der Flächeninhalt des Einheitskreises ist, sodass (z. B.) die Fläche eines Viertels des Einheitskreises \( \pi/4 \) beträgt. Das, so wird behauptet, ist ein genauso gutes Argument für \( \pi \) wie das Bogenmaß für \( \tau \). Unglücklicherweise, wie in Section 3 angemerkt und erneut in Gleichung (18) zu sehen ist, tritt der Faktor \( 1/2 \) auf natürliche Art und Weise in Zusammenhang mit dem Kreisinhalt auf. Tatsächlich lautet die Formel für die Fläche eines Kreissektors, der durch den Winkel \( \theta \) begrenzt wird
also gibt es im Allgemeinen keine Möglichkeit, den Faktor \( 1/2 \) zu vermeiden. (Wir sehen also, dass \( A = \frac{1}{2} \tau r^2 \) einfach der Spezialfall \( \theta = \tau \) ist.)
Kurz gefasst, der Unterschied zwischen Winkelmaß und Fläche ist nicht willkürlich. Es gibt keinen natürlichen Faktor \( 1/2 \) bei Winkelmaßen. Im Gegensatz dazu taucht der Faktor \( 1/2 \) bei Flächen durch das Integral einer linearen Funktion in Verbindung mit einer einfachen quadratischen Form auf. Die Argumente für \( \pi \) sind sogar noch schlechter, als es auf den ersten Blick aussieht, wie im nächsten Abschnitt gezeigt wird.
5 Pi und Tau auf den Grund gehen
Ich bin weiterhin beeindruckt davon, wie reichhaltig dieses Thema ist, und mein Verständnis von \( \pi \) und \( \tau \) hat sich über den originalen Tau-Tag hinaus weiterentwickelt. Bemerkenswert ist der Halb-Tau-Tag 2012, an dem ich eine Offenbarung darüber hatte, was genau falsch ist an \( \pi \). Das Argument beruht auf einer Analyse der Fläche und des Volumens einer \( n \)-dimensionalen Kugel und stellt klar, dass \( \pi \) in seiner typischen Definition keinerlei fundamentale geometrische Bedeutung hat.
Dieser Abschnitt behandelt weiter fortgeschrittenes Material und kann übersprungen werden, ohne den Faden zu verlieren; wenn Du ihn verwirrend findest, empfehle ich, direkt zur Schlussfolgerung in Abschnitt 6 zu springen. Aber wenn Du eine mathematische Herausforderung magst, lade ich dich ein, fortzufahren…
5.1 Oberfläche und Volumen einer Hyperkugel
Wir starten unsere Untersuchung mit der Verallgemeinerung eines Kreises auf beliebig viele Dimensionen. Dieses Objekt, auch Hypersphäre genannt, kann wie folgt definiert werden. (Der Einfachkeit halber nehmen wir an, dass diese Sphären um den Ursprung des Koordinatensystems zentriert sind.) Eine \( 0 \)-Sphäre ist die Menge aller Punkte mit der Eigenschaft
welche aus den zwei Punkten \( \pm r \) besteht. Diese Punkte bilden den Rand eines (abgeschlossenen) \( 1 \)-Kugelkörpers, das heißt der Menge aller Punkte mit der Eigenschaft
Das ist ein Liniensegment von \( -r \) bis \( r \); äquivalent ist es das abgeschlossene Intervall \( [-r, r] \).
Eine \( 1 \)-Sphäre ist ein Kreis, das heißt die Menge aller Punkte mit der Eigenschaft
Diese Figur bildet den Rand eines \( 2 \)-Kugelkörpers, das heißt der Menge aller Punkte gegeben durch
Dies ist die abgeschlossene Scheibe mit Radius \( r \); so wird ersichtlich, dass die „Kreisfläche“ richtiger definiert wird als die Fläche eines \( 2 \)-Kugelkörpers. Ähnlich dazu ist eine \( 3 \)-Sphäre (auch einfach „Sphäre“ oder „Kugelfläche“ genannt) die Menge aller Punkte mit der Eigenschaft
was die Oberfläche einer \( 3 \)-Kugel entspricht, also der Menge aller Punkte mit Eigenschaft
Die Verallgemeinerung auf beliebige \( n \), wenngleich für \( n > 3 \) schwierig zu visualisieren, ist klar: eine \( (n-1) \)-Sphäre ist die Menge aller Punkte mit der Eigenschaft
und bildet die Oberfläche des entsprechenden \( n \)-Kugelkörpers, welcher ist die Menge aller Punkte mit der Eigenschaft
Das „Volumen einer Hyperkugel“ der Dimension \( n-1 \) ist nun definiert als das Volumen \( V_n(r) \) des entsprechenden \( n \)-dimensionalen Kugelkörpers. Man erhält es durch Integration der Oberfläche \( A_{n-1}(r) \) bei jedem Radius via \( V_n(r) = \int A_{n-1}(r)\,dr \).
Wir werden gelegentlich \( A_{n-1} \) als die Oberfläche einer \( n \)-dimensionalen Kugel bezeichnen, aber strenggenommen ist es die Fläche des Randes der Kugel, also der \( (n-1) \)-dimensionalen Sphäre. Die Indizes von \( V_n \) und \( A_{n-1} \) sind so gewählt, dass sie immer der Dimensionalität des bezeichneten geometrischen Objektes entsprechen;18 der Fall \( n = 2 \) entspricht einer Scheibe (Dimensionalität \( 2 \)) und einem Kreis (Dimensionalität \( 2 - 1 = 1 \)). Dementsprechend ist \( V_2 \) das „Volumen“ des \( 2 \)-Kugelkörpers (also die Fläche einer Scheibe, umgangssprachlich auch „Fläche eines Kreises“ genannt) und \( A_{2-1} = A_1 \) ist die „Oberfläche“ einer \( 1 \)-Sphäre (also der Umfang eines Kreises). Im Zweifelsfall kann man sich einfach daran erinnern, dass \( n \) sich immer auf die Dimensionalität des Kugelkörpers bezieht, während \( n-1 \) die Dimensionalität von dessen Rand ist.
Nun, das Pi-Manifest (diskutiert in Abschnitt 4.2) verwendet eine Formel für das Volumen einer \( n \)-Einheitskugel als Argument zu Gunsten von \( \pi \):
mit der Gammafunktion aus Gleichung (16). Gleichung (19) ist ein Spezialfall der Formel für einen allgemeinen Radius, welche auch üblicherweise mit \( \pi \) ausgedrückt wird:
Weil \( V_n(r) = \int A_{n-1}(r)\,dr \), haben wir \( A_{n-1}(r) = dV_n(r)/dr \), wodurch die Oberfläche wie folgt geschrieben werden kann:
Anstatt diese Formel einfach als gegeben anzunehmen, wollen wir sehen, ob wir sie entwirren können, um mehr Licht ins Dunkel rund um \( \pi \) vs. \( \tau \) zu bringen. Zu Beginn unserer Analyse stellen wir fest, dass die augenscheinliche Einfachheit der obigen Formel eine Illusion ist: die notationell einfache Gammafunktion ist nämlich ein uneigentliches Integral über einen halboffenen Definitionsbereich (Gleichung (16)), was überhaupt keine einfache Idee ist. Glücklicherweise kann die Gammafunktion in gewissen Spezialfällen vereinfacht werden. Zum Beispiel können wir für ganzzahlige \( n \) ganz einfach zeigen (mittels partieller Integration), dass
Auf diese Weise kann \( \Gamma(x) \) als Verallgemeinerung der Fakultät für reelle Argumente interpretiert werden.19
In den Formeln für \( n \)-dimensionale Oberfläche und Volumen ist das Argument von \( \Gamma \) nicht zwingend eine Ganzzahl, sondern \( \left(1 + \frac{n}{2}\right) \), also eine ganze Zahl für gerade \( n \) und eine halbe Zahl für ungerade \( n \). Dem Rechnung tragend erhält man untenstehende Formel. Sie ist aus einem Standardwerk, Wolfram MathWorld, entnommen und wird üblicherweise mit \( \pi \) geschrieben:
Die Integration über \( r \) ergibt
Lass uns Gleichung (23) genauer anschauen. Es fällt auf, dass MathWorld die Doppelfakultät \( n!! \) verwendet—erstaunlicherweise aber nur für den ungeraden Fall. (Dies ist bereits ein Hinweis auf das Folgende.) Die Doppelfakultät ist, obwohl man sie in der Mathematik selten vorfindet, elementar: sie gleicht der normalen Fakultät, doch man subtrahiert jeweils \( 2 \) statt \( 1 \), so dass z.B. \( 5!! = 5 \cdot 3 \cdot 1 \) und \( 6!! = 6 \cdot 4 \cdot 2 \). Im Allgemeinen gilt
(Definitionsgemäß ist \( 0!! = 1!! = 1 \).) Man merkt, dass Gleichung (24) auf natürliche Weise in einen geraden und ungeraden Fall aufgeteilt ist, was MathWorlds Entscheidung, sie nur im ungeraden Fall zu verwenden, umso mysteriöser macht.
Um das Mysterium zu lösen, beginnen wir mit einer genauen Betrachtung der Formel für ungerade \( n \) in Gleichung (23):
Bei der Untersuchung des Ausdrucks
fällt auf, dass er umgeschrieben werden kann zu
und hier begegnen wir unserem alten Freund \( 2\pi \).
Lass uns nun den geraden Fall aus Gleichung (23) betrachten. Wir haben bereits bemerkt, wie seltsam es ist, die normale Fakultät im geraden und die Doppelfakultät im ungeraden Fall zu verwenden. Tatsächlich lassen sich die beiden Formeln vereinheitlichen, da die Doppelfakultät bereits in zwei Fälle aufgeteilt ist, und wir können \( n!! \) in beiden Fällen als gemeinsamen Faktor ausklammern.
Gibt es denn eine Verbindung zwischen der Fakultät und der Doppelfakultät? Ja—für gerade \( n \) sind die beiden durch folgende Identität verbunden:
(Dies kann durch vollständige Induktion verifiziert werden.) Wenn man dies in die Volumenformel für gerade \( n \) aus Gleichung (23) einsetzt, ergibt sich
was eine verblüffende Ähnlichkeit hat zu
und wiederum finden wir unseren Faktor \( 2\pi \).
Wenn wir all diese Resultate zusammensetzen, sehen wir, dass Gleichung (23) umgeschrieben werden kann zu
und Gleichung (22) umgeschrieben werden kann zu
Mittels der Substitution \( \tau=2\pi \) in Gleichung (26) ergibt sich
Um die Formeln noch weiter zu vereinheitlichen, können wir die Abrundungsfunktion \( \lfloor x \rfloor \) verwenden. Dies ist schlicht die größte ganze Zahl kleiner oder gleich \( x \) (als würden die Nachkommastellen abgeschnitten, z.B. \( \lfloor 3.7 \rfloor = \lfloor 3.2 \rfloor = 3 \)). Dies ergibt
womit wir die Formel wie folgt umschreiben können:
Die Integration von Gleichung (27) im Bezug auf \( r \) ergibt dann
Im Unterschied zu der scheinbaren Einfachheit von Gleichung (20), in welcher eine riesige Menge Komplexität hinter der \( \Gamma \)-Funktion versteckt ist, braucht Gleichung (28) keine ausgefallenen Integrale—bloß die etwas exotischen, aber dennoch elementaren, Funktionen für Abrundung und Doppelfakultät.20
Rekurrenzen
Wie wir in den Gleichungen (27) und (28) gesehen haben, teilen sich die Formeln für Oberfläche und Volumen ganz natürlich in zwei Familien auf, für die Räume mit gerader beziehungsweise ungerader Dimension. Das bedeutet, dass die vierdiemsionale Oberfläche \( S_4 \) mit \( S_2 \) verwandt ist, aber nicht mit \( S_3 \), während \( S_3 \) mit \( S_1 \) und nicht mit \( S_2 \) verwandt ist (und dementsprechend für \( V \)). Wie genau sind sie verwandt?
Wir finden die Antwort, wenn wir die Rekurrenzbeziehungen zwischen den Dimensionen herleiten.21 Lass uns insbesondere die Oberfläche einer \( n \)-dimensionalen Kugel durch die Oberfläche einer \( (n-2) \)-dimensionalen Kugel teilen:
Merke, dass sich die unterschiedlichen Konstanten für gerade und ungerade \( n \) auslöschen und dadurch die Abhängigkeit von der Parität verschwindet. Auf ähnliche Weise erhalten wir für das Verhältnis der Volumen:
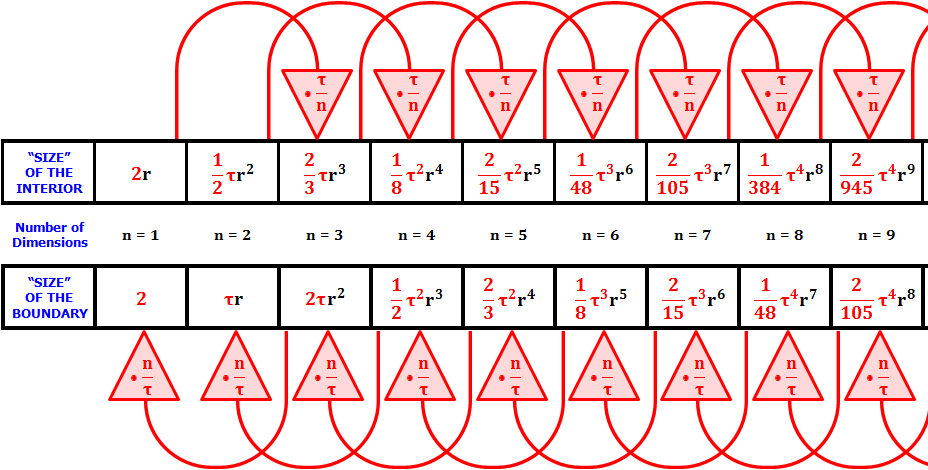
Wir sehen in den Gleichungen (29) und (30), dass wir die Oberfläche und das Volumen der \( n \)-Kugel ganz einfach erhalten, indem wir die Formel für die \( (n-2) \)-Kugel mit einem Faktor \( r^2 \) multiplizieren (dieser Faktor wird von der dimensionalen Analyse verlangt), durch \( n-2 \) respektive \( n \) dividieren und mit \( \tau \) multiplizieren. Dadurch ist \( \tau \) der rote Faden, der die beiden Lösungsfamilien für gerade und ungerade Fälle verbindet, wie es Joseph Lindenberg in Tau Before It Was Cool (Abbildung 16) illustriert.22
5.2 Drei Familien von Konstanten
Ausgerüstet mit den Werkzeugen aus Abschnitt 5.1, sind wir nun bereit dazu, \( \pi \) und \( \tau \) auf den Grund zu gehen. Um unsere Ausgrabungen abzuschließen, definieren wir mit Hilfe der Gleichungen (27) und (28) zwei Familien von Konstanten. Danach benutzen wir die Definition von \( \pi \) (Gleichung (1)), um eine dritte Familie zu definieren und dabei aufzuzeigen, was genau falsch an \( \pi \) ist.
Als Erstes definieren wir eine Familie von „Oberflächenkonstanten“ \( \tau_n \), indem wir Gleichung (27) durch \( r^{n-1} \) dividieren, also durch die Potenz von \( r \), die dazu führt, dass wir eine dimensionslose Konstante für jeden Wert von \( n \) erhalten:
Zweitens definieren wir eine Familie von „Volumenkonstanten“ \( v_n \), indem wir die Volumenformel in Gleichung (28) durch \( r^n \) teilen, damit wieder eine dimensionslose Konstante für jedes \( n \) entsteht:
Mit den beiden Familien von Konstanten aus obigen Gleichungen (31) und (32) können wir nun die Formeln für Oberfläche und Volumen (Gleichungen (27) und (27) kompakt umschreiben:
und
Dank dem Verhältnis \( V_n(r) = \int A_{n-1}(r)\,dr \), besteht die einfache Beziehung
Lass uns diese beiden Familien von Konstanten genauer betrachten. Die Familie \( \tau_{n-1} \) hat eine wichtige geometrische Bedeutung: Indem wir \( r=1 \) in Gleichung (31) einsetzen, sehen wir, dass jedes \( \tau_{n-1} \) die Oberfläche einer \( (n-1) \)-Einheitssphäre ist, was ebenfalls dem Winkelmaß einer ganzen \( (n-1) \)-Sphäre entspricht. Insbesondere erhalten wir, wenn wir \( s_{n-1}(r) \) für die \( (n-1) \)-dimensionale „Bogenlänge“ verwenden, also für den Bruchteil \( f \) der ganzen Oberfläche \( A_{n-1}(r) \), die exakte Entsprechung von Gleichung (5) in \( n \) Dimensionen:
Hier ist \( \theta_{n-1} \) einfach die allgemeine Form des Winkelmaßes in Radiant in \( n \) Dimensionen (wobei \( n \) wie gewohnt für die Dimensionalität des entsprechenden Kugelkörpers steht), und \( \tau_{n-1} \) ist die allgemeine Form von „einer Drehung“ in \( n \) Dimensionen. Im speziellen Fall \( n = 2 \) haben wir die 1-Sphären-Konstante (Kreiskonstante) \( \tau_{2-1} = \tau_1 = \tau \), was zum Diagramm in Abbildung 10 führt.
Unterdessen sind die \( v_n \) die Volumen der \( n \)-Einheitskugeln. Im Speziellen ist \( v_2 \) die Fläche der Einheitsscheibe:
Dies zeigt, dass \( v_2 = \tau/2 = 3.14159\ldots \) durchaus eine unabhängige geometrische Bedeutung zukommt. Man beachte allerdings, dass sie nichts zu tun hat mit Umfang oder Durchmesser. Anders ausgedrückt, \( \pi = C/D \) ist kein Mitglied der Familie \( v_n \).
Nun, zu welcher Familie von Konstanten gehört denn \( \pi \)? Lass uns Gleichung (1) in eine Form umschreiben, die sich einfacher auf höhere Dimensionen verallgemeinern lässt:
Wir sehen also, dass \( \pi \) natürlicherweise mit Oberflächen in Verbindung steht, dividiert durch diejenige Potenz des Durchmessers, die zu einer dimensionslosen Konstante führt. Dies legt eine dritte Familie von Konstanten nahe, \( \pi_{n-1} \):
Wir können diese Gleichung mittels der Familie \( \tau_{n-1} \) ausdrücken, wenn wir in Gleichung (33) \( D = 2r \) substituieren und Gleichung (31) anwenden:
Nun sind wir endlich an dem Punkt, wo wir genau verstehen können, was an \( \pi \) falsch ist. Die hauptsächliche geometrische Bedeutung von \( 3.14159\ldots \) ist, dass dies die Fläche der Einheitsscheibe ist. Aber diese Zahl kommt daher, dass wir \( v_n = \tau_{n-1}/n \) bei \( n=2 \) auswerten:
Es ist wahr, dass dies gerade gleich \( \pi_1 \) ist:
Aber es handelt sich dabei um einen Zufall. Die Übereinstimmung ergibt sich nur, weil \( 2^{n-1} \) zufälligerweise gleich \( n \) ist für \( n=2 \) (das heißt, \( 2^{2-1} = 2 \)). In allen höheren Dimensionen sind \( n \) und \( 2^{n-1} \) verschieden. Anders ausgedrückt: Die geometrische Bedeutung von \( \pi \) ist nichts weiter als ein mathematisches Wortspiel.
6 Fazit
Im Laufe der Jahre habe ich viele Argumente gegen die Falschheit von \( \pi \) und die Richtigkeit von \( \tau \) gehört, also gestatte mir, bevor wir unsere Diskussion beenden, einige der am häufigsten gestellten Fragen zu beantworten.
6.1 Häufig gestellte Fragen
- Meinst Du das ernst? Selbstverständlich. Ich meine, ich habe Spaß damit, und der Ton ist zeitweise unbeschwert, aber es gibt einen ernsthaften Zweck. Das Festlegen der Kreiskonstante als das Verhältnis vom Umfang zum Durchmesser ist eine umständliche und verwirrende Konvention. Obwohl ich es begrüßen würde, wenn Leute, die sich intensiver mit Mathematik befassen, ihre Gewohnheiten ändern, mache ich mir keine besonderen Sorgen um sie, denn sie können für sich selbst sorgen. Es sind die Neulinge, um die ich mir am meisten Sorgen mache, denn sie tragen die Hauptlast des Schadens: wie in Abschnitt 2.1 erwähnt, ist \( \pi \) eine pädagogische Katastrophe. Versuche, einem Zwölfjährigen (oder einem Dreißigjährigen) zu erklären, warum das Winkelmaß für ein Achtel eines Kreises—ein Stück Pizza—\( \pi/8 \) ist. Moment, ich meinte \( \pi/4 \). Verstehst Du, was ich meine? Es ist zum Verrücktwerden!
- Wie können wir von \( \pi \) zu \( \tau \) wechseln? Wenn Du das nächste Mal etwas schreibst, in dem die Kreiskonstante vorkommt, sag schlicht „Der Einfachheit halber setzen wir \( \tau = 2\pi \)“ und fahre dann wie gewohnt fort. (Natürlich könnte dies die Frage aufwerfen: „Warum würdest du das tun wollen?“, und ich gebe zu, es wäre schön, eine Stelle zu haben, auf die wir verweisen können. Wenn bloß jemand ein, sagen wir, Manifest zu diesem Thema schreiben würde…) Der beste Weg, Leute dazu zu bringen, \( \tau \) zu verwenden, ist, es selbst zu verwenden.
- Ist es nicht zu spät für einen Wechsel? Müssten nicht alle Lehrbücher und Publikationen umgeschrieben werden? Nein zu beiden Punkten. Es ist wahr, dass einige Konventionen, obgleich unglücklich gewählt, praktisch unumkehrbar sind. Zum Beispiel führt Benjamin Franklins Wahl für die Vorzeichen elektrischer Ladungen dazu, dass das bekannteste Beispiel für elektrischen Strom (nämlich freie Elektronen in Metallen) positiv ist, wenn die Ladungsträger negativ sind, und umgekehrt—und damit machen seither verwirrende negative Vorzeichen angehenden Physikstudierenden das Leben schwer.23 Um diese Konvention zu ändern, müssten alle Lehrbücher neu geschrieben (und die alten verbrannt) werden, da es unmöglich ist, auf einen Blick zu sagen, welche Konvention verwendet wird. Dementsprechend ist auch eine Neudefinition von \( \pi \) praktisch unmöglich, aber wir können im Handumdrehen von \( \pi \) zu \( \tau \) wechseln, indem wir die Konvertierung
\[ \pi \leftrightarrow \textstyle{\frac{1 }{2}}\tau \]
verwenden. Es handelt sich um eine rein mechanische Substitution, absolut robust und tatsächlich vollständig reversibel. Der Wechsel von \( \pi \) zu \( \tau \) kann also schrittweise erfolgen; Im Gegensatz zu einer Neudefinition muss dies nicht auf einmal geschehen.
- Würde \( \tau \) die Leute, besonders junge Lernende, nicht verwirren? Wer schlau genug ist, um das Bogenmaß zu verstehen, ist schlau genug, um \( \tau \) zu verstehen—und warum \( \tau \) tatsächlich weniger verwirrend ist als \( \pi \). Es ist auch an sich nichts Verwirrendes daran, „Sei \( \tau = 2\pi \)“ zu sagen, weil sich um eine einfache Substitution handelt. Schließlich können wir die Situation als Lehrgelegenheit ergreifen: Die Idee, dass \( \pi \) falsch sein könnte, ist interessant, und die Lernenden können sich mit dem Material beschäftigen, indem sie die Gleichungen in ihren Lehrbüchern von \( \pi \) in \( \tau \) umwandeln, um selbst zu sehen, welche die bessere Wahl ist.
- Spielt das wirklich irgendeine Rolle? Selbstverständlich tut es das. Die Kreiskonstante ist wichtig. Die Leute interessieren sich immerhin genug dafür, um ganze Bücher darüber zu schreiben, sie jedes Jahr an einem bestimmten Tag zu feiern und Zehntausende ihrer Ziffern auswendig zu lernen. Ich kümmere mich genug, um ein ganzes Manifest zu schreiben, und Du kümmerst dich genug, um es zu lesen. Gerade weil es wichtig ist, ist es schwer zuzugeben, dass die gegenwärtige Konvention falsch ist. (Ich meine, wie sagt man Rajveer Meena, einem Weltrekordhalter, dass er gerade 70.000 Stellen der Hälfte der wahren Kreiskonstante aufgezählt hat?) Da die Kreiskonstante wichtig ist, ist es wichtig, sie richtig hinzubekommen, und wir haben in diesem Manifest gesehen, dass die richtige Zahl \( \tau \) ist. Obwohl \( \pi \) von großer historischer Bedeutung ist, liegt die mathematische Bedeutung von \( \pi \) darin, dass es sich um die Hälfte von \( \tau \) handelt.
- Warum hat überhaupt jemand \( \pi \) verwendet? Die Ursprünge der Zahl \( \pi \) gingen wahrscheinlich im Nebel der Zeit verloren. Ich vermute, dass die Konvention, \( C/D \) anstelle von \( C/r \) zu verwenden, deshalb entstanden ist, weil es einfacher ist, den Durchmesser eines kreisförmigen Objekts zu messen als seinen Radius. Aber das macht es nicht zu guter Mathematik, und ich bin überrascht, dass Archimedes, der bekanntermaßen die Kreiskonstante approximiert hat, nicht wusste, dass \( C/r \) die wesentlichere Zahl ist. Als Notation wurde \( \pi \) vor rund 300 Jahren durch Leonhard Euler populär gemacht, basierend auf der Arbeit von William Jones. In seinem sehr einflussreichen zweibändigen Werk Introductio in analysin infinitorum zum Beispiel verwendet Euler \( \pi \), um den Halbumfang eines Einheitskreises, also das Maß für \( 180^\circ \), zu bezeichnen.24 Leider erklärt Euler nicht, wieso er diesen Faktor \( 1/2 \) einführt, doch er könnte etwas mit dem gelegentlichen Gebrauch des Semiperimeters eines Polygons zu tun haben. Jedenfalls bemerkt Euler sofort, dass der Sinus und Cosinus eine Periodenlänge von \( 2\pi \) haben, also hätte er durchaus erkennen können, dass sein Winkelmaß zweimal die Periode der Kreisfunktionen mißt, was seine Wahl umso verblüffender macht. Er hätte es allerdings fast richtig gemacht: Überraschenderweise verwendete Euler nämlich das Symbol \( \pi \) sowohl für \( 3.14\ldots \) als auch für \( 6.28\ldots \) zu unterschiedlichen Zeiten!25 Schade, dass er sich nicht für die bequemere Wahl entschieden hat.
- Warum interessierst du dich dafür? Erstens ist mir als Wahrheitssuchender die Korrektheit der Erklärung wichtig. Zweitens ist mir als Mentor die Klarheit der Darstellung wichtig. Drittens liebe ich als Hacker einen guten Hack. Viertens finde ich es als Student der Geschichte und der menschlichen Natur faszinierend, dass die Absurdität von \( \pi \) jahrhundertelang offenkundig lag, bevor irgendjemand es zu bemerken schien. Darüber hinaus gehören viele der Menschen, welche die wahre Kreiskonstante verfehlt haben, zu den rationalsten und intelligentesten, die je gelebt haben. Was könnte uns sonst noch ins Gesicht starren und nur darauf warten, dass wir es entdecken?
- Bist du verrückt? Das geht Dich wirklich nichts an, aber nein. Ich habe zwar so wie alle Menschen meine Eigenheiten, bin aber dem äußeren Anschein nach in praktisch jeder Hinsicht normal. Wenn Du mich triffst, würdest Du nie vermuten, dass ich kein gewöhnlicher Bürger, sondern ein notorischer mathematischer Propagandist bin.
- Aber was ist mit den Wortspielen? Und nun kommen wir zum letzten Einwand. Ich weiß, ich weiß, „\( \pi \) in the sky“ ist wirklich genial. Und doch steckt \( \tau \) selbst voller Möglichkeiten. \( \tau \)ismus sagt uns: Es ist nicht \( \tau \), das ein Stück von \( \pi \) ist, sondern \( \pi \), das ein Stück von \( \tau \) ist—ein halbes \( \tau \), um genau zu sein. Die Identität \( e^{i\tau} = 1 \) sagt: „Sei eins mit dem \( \tau \).“ Und obwohl sich die Feststellung „Eine Drehung um eine Runde ist 1“ anhört wie eine \( \tau \)-tologie, ist es die wahre Natur des \( \tau \). Während wir diese betrachten, um den Weg des \( \tau \) zu suchen, müssen wir uns daran erinnern, dass \( \tau \)ismus auf Vernunft basiert, nicht auf Glaube: Gefolgsleute des \( \tau \)ismus sind niemals \( \pi \)etätvoll.
6.2 Nimm das Tau an
Wir haben im Tau-Manifest gesehen, dass die naturgemäße Wahl für die Kreiskonstante das Verhältnis des Kreisumfangs nicht zum Kreisdurchmesser, sondern zu seinem Radius ist. Diese Zahl braucht einen Namen und ich hoffe, Du wirst sie mit mir \( \tau \) nennen:
Die Verwendung ist ganz natürlich, die Motivation ist eindeutig und die Auswirkungen sind tiefgreifend. Außerdem kommt sie mit einem ziemlich coolen Diagramm (Abbildung 17). In Abbildung 17 sehen wir eine Bewegung durch Yang („hell, weiß, aufwärts“) zu \( \tau/2 \) und eine Rückkehr durch Yin („dunkel, schwarz, abwärts“) zurück zu \( \tau \).26 Wenn wir \( \pi \) statt \( \tau \) verwenden, ist es, als hätten wir Yang ohne Yin.

6.28 Tau-Tag
Das Tau-Manifest wurde das erste Mal am Tau-Tag, dem 28. Juni (6/28) 2010, veröffentlicht. Der Tau-Tag ist ein Tag, an dem man sich an allen mathematischen Dingen erfreut und diese feiert.27 Wenn Du Updates zu \( \tau \), einschließlich Benachrichtigungen über mögliche zukünftige Tau-Tag-Veranstaltungen, erhalten möchtest, dann tritt bitte der Tau-Manifest Mailingliste auf tauday.com bei.28 Und falls Du der Meinung bist, dass die runden Backwaren am Pi-Tag schmackhaft sind, warte einfach noch ein bisschen—am Tau-Tag gibt es doppelt so viel Pi(e)!
Share the τ Manifesto
6.283 Danksagungen
Zuallererst möchte ich Bob Palais dafür danken, dass er „\( \pi \) Is Wrong!“ geschrieben hat. Ich kann mich nicht mehr erinnern, wie stark mein Misstrauen gegenüber \( \pi \) gewesen ist, bevor ich an diesen Artikel geraten bin, aber „\( \pi \) Is Wrong!“ hat mir definitiv die Augen geöffnet, und jeder Abschnitt des Tau-Manifests schuldet ihm Dankbarkeit. Ich möchte Bob auch für seine hilfreichen Kommentare zu diesem Manifest danken und insbesondere dafür, dass er so ein guter Kumpel ist.
Ich habe nun schon eine Zeit lang über das Tau-Manifest nachgedacht und viele der hier vorgestellten Ideen sind im Zuge von Gesprächen mit meinem Freund Sumit Daftuar entstanden. Er diente dabei als Resonanzboden und gelegentlich als Fürsprecher des Teufels. Seine Kenntnisse als Lehrer und Mathematiker beeinflussen mein Denken in vielerlei Hinsicht.
Ich habe auch Ermutigung und hilfreiches Feedback von mehreren Leuten aus dem Lesepublikum erhalten. Ich möchte Vi Hart und Michael Blake für ihre wunderbaren \( \tau \)-inspirierten Videos danken, sowie Don „Blue“ McConnell und Skona Brittain für ihre Hilfe, \( \tau \) zu einem Teil der Geek-Kultur zu machen (durch die Zeit-in-\( \tau \) iPhone-App, beziehungsweise die Tau-Uhr). Die angenehme Interpretation des Yin-Yang-Symbols auf dem Cover des Tau-Manifests geht auf eine Anregung von Peter Harremoës zurück. Er hat, wie oben erwähnt, die seltene Auszeichnung, unabhängig davon vorgeschlagen zu haben, \( \tau \) für die Kreiskonstante zu verwenden. Ein weiterer \( \tau \)ist vor der Erscheinung des Manifests, Joseph Lindenberg, ist ebenfalls ein überzeugter Unterstützer und sein Enthusiasmus ist sehr geschätzt.
Ich habe mehrere gute Vorschläge von Christopher Olah erhalten, insbesondere in Bezug auf die geometrische Interpretation der Eulerschen Identität; Der Abschnitt 2.3.2 über Eulersche Identitäten wurde durch einen exzellenten Vorschlag von Timothy „Patashu“ Stiles inspiriert. Don Blaheta hat Teile des Materials über Hyperspheren vorausgeahnt und angeregt und John Kodegadulo hat es besonders anschaulich und unterhaltsam zusammengestellt. Dann hat Jeff Cornell als wunderbare Verfeinerung die Gleichung \( \lambda = \tau/4 \) eingeführt, und Hjalmar Peters hat zu einer besseren Präsentation beigetragen, indem er mich überzeugt hat, dieses Material prägnanter zu fassen.
Ich möchte auch den freiwilligen Übersetzern danken, die das Tau-Manifest in so vielen verschiedenen Sprachen zur Verfügung gestellt haben: Juan Guijarro Ferreiro (Spanisch); Daniel Rosen und Alexis Drai (Französisch); Andrea Laretto (Italienisch); Gustavo Chaves (Portugiesisch); Axel Scheithauer, Jonas Wagner und Johannes Clemens Huber, mit hilfreichen Anmerkungen von Caroline Steiblin (Deutsch); Aleksandr Alekseevich Adamov (Russisch); und Daniel Li Qu (vereinfachtes Chinesisch).
Zuguterletzt möchte ich Wyatt Greene danken, und zwar unter anderem für sein außergewöhnlich hilfreiches Feedback zum Pre-Launch-Entwurf des Manifests. Falls Ihr jemals jemanden braucht, um euch zu sagen „So ziemlich alles des [mittlerweile gelöschten] letzten Abschnitts ist totaler Mist“, dann ist Wyatt Euer Mann.
6.28318 Copyright
Das Tau-Manifest. Copyright © 2010–2022 Michael Hartl. Bitte zögert nicht, das Tau-Manifest PDF29 für Bildungszwecke zu verteilen, und erwägt den Kauf eines oder mehrerer Exemplare der Druckausgabezur Verteilung an Lernende und andere Interessierte.
6.283185 Widmung
Das Tau-Manifest ist Harry „Woody“ Woodworth, meinem Naturwissenschaftslehrer der achten Klasse, gewidmet. Obwohl ich im Laufe Jahre dankbarerweise Unterstützung von vielen Lehrkräften erhalten habe, hat Woody außergewöhnlich, ja sogar irrational (wage ich zu sagen transzendent?) an mein Potential geglaubt und zuversichtlich vorhergesagt, dass „sie eines Tages die ‚Hartl-Theorie‘ in Schulen unterrichten werden.“ In Anbetracht dessen, wie viele Mathematiklehrkräfte sich gemeldet haben, um das Tau-Manifest zu unterstützen, nehme ich an, dass Woodys Vorhersage nun in gewisser Weise eingetreten ist.
20. Tau-Korrespondent Jeff Cornell hat aufgezeigt, dass Gleichung (27) und Gleichung (28) noch weiter vereinfacht werden können, wenn man ein Maß für den rechten Winkel einführt. Er nennt dieses Maß lambda: \( \lambda \equiv \tau/4 \). Dadurch wird die Abhängigkeit von der Parität von der Abrundungsfunktion absorbiert:
und
Meines Wissens nach ist dies die kompakteste Form der Formeln für Oberfläche und Volumen. Ihre Einfachheit kostet uns einen Faktor \( 2^n \), doch dieser hat eine klare geometrische Bedeutung: Eine Kugel in \( n \) Dimensionen lässt sich ganz natürlich in \( 2^n \) kongruente Stücke aufteilen, entsprechend den \( 2^n \) Familien von Lösungen der Gleichung \( \sum_{i=1}^{n} x_i^2 = r^2 \) (eine für jede mögliche Wahl von \( \pm x_i \)). In zwei Dimensionen sind das die vier Quadranten. In drei Dimensionen sind es die acht Oktanten, und so weiter für höhere Dimensionen. Nichtsdestotrotz ist eine Abhängigkeit von der Parität real und unvermeidbar (siehe z.B. Abbildung 16), und deshalb schreiben wir die Formeln weiterhin mit \( \tau \), wie in Gleichung (27) und Gleichung (28).

