1 La costante del cerchio
Il Tau Manifesto è dedicato a uno dei numeri più importanti della matematica, forse il più importante: la costante del cerchio che mette in relazione la circonferenza di un cerchio con la sua dimensione lineare. Per millenni, il cerchio è stato considerato la più perfetta delle forme, e la costante del cerchio ne cattura la geometria in un unico numero. Ovviamente, la scelta tradizionale per tale costante è \( \pi \) (pi)—ma, come il matematico Bob Palais fa notare nel suo delizioso articolo “\( \pi \) Is Wrong!”,1 \( \pi \) è sbagliato. È ora di mettere le cose a posto.
1.1 Una proposta immodesta
Iniziamo a riparare il danno portato da \( \pi \) cercando come prima cosa di capire il famosissimo numero vero e proprio. La definizione tradizionale per la costante del cerchio definisce \( \pi \) come il rapporto fra la circonferenza del cerchio (la lunghezza) e il suo diametro (la larghezza):2
Il numero \( \pi \) ha moltissime proprietà interessanti—oltre a molte altre cose, è irrazionale e trascendente—e la sua diffusa presenza nelle formule matematiche è ben conosciuta.
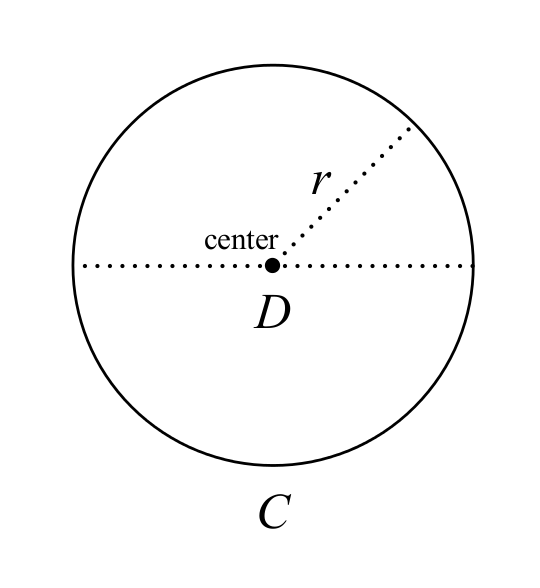
Dovrebbe essere ovvio che \( \pi \) non è “sbagliato” nel senso di essere oggettivamente sbagliato; il numero \( \pi \) è perfettamente ben definito, e possiede tutte le proprietà che i matematici gli attribuiscono normalmente. Quando diciamo che “\( \pi \) è sbagliato”, intendiamo che \( \pi \) è una scelta che confonde ed è innaturale per la costante del cerchio. In particolare, un cerchio è definito come l’insieme dei punti a una distanza fissa, il raggio, da un punto dato, il centro (Figura 1). Mentre ci sono infinite forme con larghezza costante (Figura 2),3 ne esiste una sola con raggio costante. Ciò suggerisce che una definizione più naturale per la costante del cerchio potrebbe utilizzare \( r \) invece che \( D \):
Poiché il diametro di un cerchio è il doppio del suo raggio, tale numero è numericamente uguale a \( 2\pi \). Come \( \pi \), è trascendente e dunque irrazionale, e (come vedremo in Sezione 2) il suo uso in matematica è altrettanto diffuso.
In “\( \pi \) Is Wrong!”, Bob Palais argomenta con persuasione in favore della seconda di queste due definizioni per la costante del cerchio, e secondo la mia prospettiva egli ha avuto il merito più grande nell’identificare questo problema e presentarlo a un pubblico più ampio. Egli chiama la vera costante del cerchio “un giro”, e introduce anche un nuovo simbolo per rappresentarla (Figura 3). Come vedremo, la sua descrizione è preveggente, ma sfortunatamente il simbolo è relativamente strano, e (come discusso in Sezione 4) sembra improbabile che possa ottenere grande adozione.

Il Tau Manifesto è dedicato a sostenere il fatto che la risposta migliore a “\( \pi \) è sbagliato” sia “No, davvero.” E che la vera costante del cerchio meriti un nome adeguato. Come si sarà potuto immaginare, Il Tau Manifesto propone che tale nome debba essere la lettera greca \( \tau \) (tau):
Per tutto il resto di questo manifesto, vedremo che il numero \( \tau \) è la scelta corretta, e mostreremo tramite il suo utilizzo (Sezione 2 e Sezione 3) e per argomentazione diretta (Sezione 4) che la lettera \( \tau \) è anch’essa una scelta naturale.
1.2 Un potente nemico
Prima di procedere con la dimostrazione che \( \tau \) è la scelta naturale per la costante del cerchio, dobbiamo innanzitutto realizzare con cosa abbiamo a che fare—e che esiste una potente cospirazione, da più di cento anni, determinata a diffondere propaganda pro-\( \pi \). Interi libri sono stati scritti inneggiando alle virtù di \( \pi \). (Voglio dire, libri interi!) E la devozione irrazionale a \( \pi \) si è diffusa anche ai più alti livelli di geekdom; ad esempio, nel “Pi Day” 2010 Google ha cambiato il proprio logo per onorare \( \pi \) (Figura 4).
Nel mentre, alcune persone memorizzano decine, centinaia, persino migliaia di cifre di questo mistico numero. Quale poveraccio memorizzerebbe persino 40 cifre di \( \pi \) (Figura 5)?4
Davvero, i sostenitori di \( \tau \) hanno a che fare con un audace nemico. Eppure abbiamo un potente alleato—la verità è al nostro fianco.
2 Il numero tau
Abbiamo visto nella Sezione 1.1 che il numero \( \tau \) può anche essere scritto come \( 2\pi \). Come indicato in “\( \pi \) Is Wrong!”, è dunque di grande interesse scoprire che la combinazione \( 2\pi \) appare in tutta la matematica con una frequenza sorprendente. Ad esempio, consideriamo gli integrali su tutto lo spazio in coordinate polari:
Il limite superiore dell’integrazione su \( \theta \) è sempre \( 2\pi \). Lo stesso fattore appare nella definizione della distribuzione (normale) gaussiana,
e ancora nella trasformata di Fourier,
Ricorre nella formula integrale di Cauchy,
nelle radici \( n \)-esime dell’unità,
e nei valori della funzione zeta di Riemann per numeri interi positivi:5
Queste formule non sono state scelte apposta—aprite i vostri libri di matematica o fisica preferiti e provate voi stessi. Ci sono molti altri esempi, e la conclusione è chiara: c’è qualcosa di speciale in \( 2\pi \).
Per giungere al fondo di questo mistero, dobbiamo ritornare alle origini considerando la natura dei cerchi, e specialmente la natura degli angoli. Anche se è probabile che parecchi di questi argomenti siano a voi familiari, vale la pena rivisitarli, poiché è proprio qui che inizia la vera comprensione di \( \tau \).
2.1 Cerchi ed angoli
C’è una stretta connessione tra cerchi e angoli, come mostrato in Figura 6. Dato che i cerchi concentrici in Figura 6 hanno raggi differenti, le linee in figura dividono lunghezze d’arco differenti, ma l’angolo \( \theta \) (theta) è lo stesso in entrambi i casi. In altre parole, l’ampiezza dell’angolo non dipende dal raggio del cerchio utilizzato per definire l’arco. Il compito principale nella misurazione degli angoli è quella di creare un sistema che catturi questa indipendenza dal raggio.

Probabilmente il sistema angolare più semplice è quello dei gradi, che dividono un cerchio in 360 parti uguali. Un risultato di questo sistema è l’insieme di angoli notevoli (familiare agli studenti di trigonometria) mostrato in Figura 7.

Un sistema più fondamentale per misurare gli angoli consiste in un confronto diretto della lunghezza d’arco \( s \) con il raggio \( r \). Nonostante le lunghezze in Figura 6 siano differenti, la lunghezza d’arco cresce in proporzione al raggio, dunque il rapporto tra la lunghezza d’arco e il raggio è la stessa in entrambi i casi:
Questo suggerisce la seguente definizione di misurazione in radianti:
Questa definizione ha la proprietà desiderata di indipendenza dal raggio, e dato che sia \( s \) che \( r \) hanno come unità di misura una lunghezza, i radianti sono adimensionali per costruzione. L’uso dei radianti come unità di misura degli angoli porta a formule eleganti e succinte in tutta la matematica; ad esempio, la classica formula per la derivata di \( \sin\theta \) è vera solo quando \( \theta \) è espresso in radianti:
Naturalmente, gli angoli notevoli in Figura 7 possono essere espressi in radianti, e quando avete fatto trigonometria alle superiori, avrete probabilmente memorizzato i valori speciali mostrati in Figura 8. (chiameremo questo sistema di misurazione \( \pi \)-radianti per enfatizzare che sono scritti in termini di \( \pi \).)


Ora, un momento di riflessione mostra che i cosiddetti angoli “notevoli” sono solo frazioni razionali particolarmente semplici del cerchio, come mostrato in Figura 9. Ciò suggerisce di rivisitare l’Eq. (4), riscrivendo la lunghezza d’arco \( s \) in termini della frazione \( f \) sull’intera circonferenza \( C \), i.e., \( s = f C \):
Notare come \( \tau \) derivi naturalmente da questa analisi. Se siete credenti in \( \pi \), temo che il risultante diagramma degli angoli notevoli (Figura 10) possa scuotere la vostra fede nel profondo.

Pur essendoci molti altri punti in favore di \( \tau \), la Figura 10 è probabilmente la più suggestiva. Vediamo anche dalla Figura 10 il genio nell’identificazione di Bob Palais della costante del cerchio come “un giro”: \( \tau \) è la misura dell’angolo in radianti per l’angolo giro di un cerchio. Inoltre, con \( \tau \) non c’è niente da memorizzare: un dodicesimo di un giro è \( \tau/12 \), un ottavo di un giro è \( \tau \)/8, e così via. Usare \( \tau \) ci dà il meglio dei due mondi combinando chiarezza concettuale con tutti i benefici concreti dei radianti; per esempio, il significato astratto di \( \tau \)/12 è ovvio, ma è anche semplicemente un numero:
Infine, confrontando la Figura 8 con la Figura 10, vediamo anche da dove arrivano quei fastidiosi fattori di \( 2\pi \): un giro del cerchio è \( 1\tau \), ma \( 2\pi \). Numericamente sono uguali, ma concettualmente sono abbastanza distinti.
Le ramificazioni
I fattori \( 2 \) non necessari che derivano dall’uso di \( \pi \) sono di per sé abbastanza noiosi, ma ancor più importante è la loro tendenza a semplificarsi quando divisi da un qualsiasi altro numero pari. Questi risultati assurdi, come mezzo \( \pi \) per indicare un quarto di giro, nascondono la relazione sottostante tra la misurazione degli angoli e la costante del cerchio. A coloro che sostengono che “non ha importanza” se utilizziamo \( \pi \) o \( \tau \) quando insegniamo trigonometria, chiedo semplicemente di guardare Figura 8, Figura 9, e Figura 10 con gli occhi di un bambino. Vedrete che, dal punto di vista di un principiante, usare \( \pi \) invece che \( \tau \) è un disastro pedagogico.
2.2 Le funzioni del cerchio
Anche se la misurazione in radianti fornisce una delle argomentazioni più convincenti per la vera costante del cerchio, vale la pena comparare le virtù di \( \pi \) e \( \tau \) anche in altri contesti. Iniziamo considerando le importanti funzioni elementari \( \sin\theta \) e \( \cos\theta \). Conosciute come le “funzioni del cerchio” dato che forniscono le coordinate di un punto sulla circonferenza unitaria (i.e., la circonferenza di un cerchio di raggio \( 1 \)), seno e coseno sono le funzioni fondamentali della trigonometria (Figura 11).

Esaminiamo i grafici delle funzioni del cerchio per comprendere meglio il loro comportamento.6 Potrete notare dalla Figura 12 e dalla Figura 13 che entrambe le funzioni sono periodiche con periodo \( T \). Come mostrato in Figura 12, la funzione seno \( \sin\theta \) inizia a zero, raggiunge un massimo a un quarto di periodo, passa attraverso zero a metà periodo, raggiunge un minimo a tre quarti di periodo, e ritorna a zero dopo un intero periodo. Al contempo, la funzione coseno \( \cos\theta \) inizia da un massimo, ha un minimo a metà periodo, e passa attraverso zero a un quarto e tre quarti di periodo (Figura 13). Per riferimento, entrambe le figure mostrano i valori di \( \theta \) (in radianti) in ogni punto notevole.


Ovviamente, dato che sia seno che coseno compiono un intero ciclo durante un giro del cerchio, abbiamo che \( T = \tau \); i.e., le funzioni del cerchio hanno periodo uguale alla costante del cerchio. Di conseguenza, gli “speciali” valori notevoli di \( \theta \) sono assolutamente naturali: un quarto di periodo è \( \tau/4 \), metà periodo è \( \tau/2 \), eccetera. Ed infatti, mentre disegnavo la Figura 12, mi son ritrovato a chiedermi quale fosse il valore numerico di \( \theta \) per lo zero della funzione seno. Dato che lo zero compare dopo metà periodo, e dato che \( \tau \approx 6.28 \), un veloce calcolo a mente porta al seguente risultato:
Proprio così: sono rimasto sbalordito nello scoprire che mi ero già dimenticato che \( \tau/2 \) è ogni tanto anche chiamato “\( \pi \)”. Magari è successa una cosa del genere anche a voi proprio adesso. Benvenuti nel mio mondo.
2.3 L’identità di Eulero
Sarei negligente se non mi occupassi in questo manifesto dell’identità di Eulero, a volte chiamata “la più elegante equazione della matematica”. Questa identità riguarda la funzione esponenziale complessa, la quale è profondamente collegata sia alle funzioni del cerchio che alla geometria del cerchio stesso.
In funzione della strada intrapresa, la seguente equazione può essere dimostrata come teorema o presa come definizione; in ogni caso, è un risultato particolarmente notevole:
Conosciuta come la formula di Eulero (dal matematico Eulero), questa equazione mette in relazione un esponenziale con argomento immaginario con le funzioni del cerchio seno e coseno e l’unità immaginaria \( i \). Nonostante la giustificazione della formula di Eulero sia al di là della portata di questo manifesto, la sua provenienza è al di sopra di ogni sospetto, e la sua importanza resta fuori discussione.
Calcolare l’Eq. (5) in \( \theta = \tau \) fornisce l’identità di Eulero:7
A parole, l’Eq. (6) fornisce la seguente osservazione fondamentale:
L’esponenziale complesso della costante del cerchio è l’unità.
Geometricamente, moltiplicare per \( e^{i\theta} \) corrisponde a ruotare un numero complesso per un angolo \( \theta \) nel piano complesso, il che suggerisce una seconda interpretazione dell’identità di Eulero:
Una rotazione di un giro è 1.
Dato che il numero \( 1 \) è l’identità moltiplicativa, il significato geometrico di \( e^{i\tau} = 1 \) è che ruotare un punto nel piano complesso di un giro semplicemente lo fa ritornare nella sua posizione originale.
Come nel caso della misurazione in radianti, notiamo quanto l’associazione tra \( \tau \) e un giro del cerchio sia naturale. In effetti, l’identificazione di \( \tau \) con “un giro” fa sembrare l’identità di Eulero quasi una tautologia.8
Non esattamente l’equazione più bella
Ovviamente, la forma tradizionale dell’identità di Eulero è scritta in termini di \( \pi \) invece che di \( \tau \). Per derivarla, iniziamo valutando la formula di Eulero in \( \theta = \pi \), che porta a
Quel segno meno è così scomodo che l’Eq. (7) è quasi sempre riarrangiata immediatamente, portando alla seguente “meravigliosa” equazione:
A questo punto, colui che la espone solitamente fa qualche dichiarazione altisonante su come l’Eq. (8) metta in relazione \( 0 \), \( 1 \), \( e \), \( i \), e \( \pi \)—a volte chiamati come i “cinque più importanti numeri della matematica”.
In questo contesto, è sorprendente quante persone si lamentino del fatto che l’Eq. (6) metta in relazione solo quattro di queste cinque. Bene:
L’Eq. (9), senza essere riarrangiata, relaziona davvero i cinque numeri più importanti della matematica: \( 0 \), \( 1 \), \( e \), \( i \), e \( \tau \).
Identità euleriane
Dato che si può aggiungere zero ovunque in qualsiasi equazione, l’introduzione di \( 0 \) nell’Eq. (9) è una sorta di contrappunto ironico a \( e^{i\pi} + 1 = 0 \), ma l’identità \( e^{i\pi} = -1 \) ha davvero un qualcosa di importante da dire. Osserviamo cosa succede quando la riscriviamo in termini di \( \tau \):
Geometricamente, questa equazione ci dice che una rotazione di metà turno è la stessa cosa che moltiplicare per \( -1 \). Ed effettivamente è proprio così: con una rotazione di \( \tau/2 \) radianti, il numero complesso \( z = a + ib \) viene mappato a \( -a - ib \), che è in effetti semplicemente \( -1\cdot z \).
Riscritta in termini di \( \tau \), osserviamo che la versione “originale” dell’identità di Eulero (Eq. (7)) possiede un evidente significato geometrico che manca quando scritta in termini di \( \pi \). (Ovviamente, \( e^{i\pi} = -1 \) può essere interpretata come una rotazione di \( \pi \) radianti, ma la riscrittura quasi universale nell’arrivare a \( e^{i\pi} + 1 = 0 \) mostra come usare \( \pi \) distragga dal significato geometrico naturale dell’identità.) Le identità con un quarto di angolo hanno interpretazioni geometriche simili: calcolare l’Eq. (5) in \( \tau/4 \) dà \( e^{i\tau/4} = i \), che semplicemente dice che un quarto di giro nel piano complesso è lo stesso che moltiplicare per \( i \); allo stesso modo, \( e^{i\cdot(3\tau/4)} = -i \) indica che tre quarti di un giro è lo stesso che moltiplicare per \( -i \). Un riassunto di questi risultati, che chiameremo identità euleriane, si trova in Tabella 1.
| Angolo di rotazione | Identità euleriana | ||
| \( 0 \) | \( e^{i\cdot0} \) | \( = \) | \( 1 \) |
| \( \tau/4 \) | \( e^{i\tau/4} \) | \( = \) | \( i \) |
| \( \tau/2 \) | \( e^{i\tau/2} \) | \( = \) | \( -1 \) |
| \( 3\tau/4 \) | \( e^{i\cdot(3\tau/4)} \) | \( = \) | \( -i \) |
| \( \tau \) | \( e^{i\tau} \) | \( = \) | \( 1 \) |
Possiamo portare questa analisi un ulteriore passo avanti notando che, per ogni angolo \( \theta \), \( e^{i\theta} \) può essere interpretato come un punto sulla circonferenza unitaria nel piano complesso. Dato che il piano complesso identifica l’asse orizzontale con la parte reale del numero e l’asse verticale con la parte immaginaria, la formula di Eulero ci dice che \( e^{i\theta} \) corrisponde alle coordinate \( (\cos\theta, \sin\theta) \). Inserendo i valori degli angoli “speciali” della Figura 10 nella Eq. (5) si ottengono i punti mostrati in Tabella 2, e riportandoli nel piano complesso ricaviamo la Figura 14. Un confronto di Figura 14 con Figura 10 toglie velocemente ogni dubbio su quale scelta della costante del cerchio riveli al meglio la relazione fra la formula di Eulero e la geometria del cerchio.
| Forma polare | Forma rettangolare | Coordinate |
| \( e^{i\theta} \) | \( \cos\theta + i\sin\theta \) | \( (\cos\theta, \sin\theta) \) |
| \( e^{i\cdot0} \) | \( 1 \) | \( (1, 0) \) |
| \( e^{i\tau/12} \) | \( \frac{\sqrt{3}}{2} + \frac{1}{2}i \) | \( (\frac{\sqrt{3}}{2}, \frac{1}{2}) \) |
| \( e^{i\tau/8} \) | \( \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i \) | \( (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) \) |
| \( e^{i\tau/6} \) | \( \frac{1}{2} +\frac{\sqrt{3}}{2} i \) | \( (\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( e^{i\tau/4} \) | \( i \) | \( (0, 1) \) |
| \( e^{i\tau/3} \) | \( -\frac{1}{2} +\frac{\sqrt{3}}{2} i \) | \( (-\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( e^{i\tau/2} \) | \( -1 \) | \( (-1, 0) \) |
| \( e^{i\cdot(3\tau/4)} \) | \( -i \) | \( (0, -1) \) |
| \( e^{i\tau} \) | \( 1 \) | \( (1, 0) \) |

3 L’area del cerchio: il colpo di grazia
Se siete arrivati fin qui come credenti in \( \pi \), sicuramente starete mettendo in dubbio la vostra fede. \( \tau \) è così naturale, il suo significato così trasparente—c’è forse qualche esempio in cui \( \pi \) risplende in tutta la sua gloria? Forse un qualche ricordo—sì, c’è una formula—è la formula per l’area del cerchio! Ammirate:
No, un attimo. La formula dell’area è sempre scritta in termini del raggio, in questo modo:
Qui vediamo \( \pi \), disadorno, in una delle equazioni più importanti della matematica—una formula dimostrata per la prima volta da Archimede stesso. L’ordine è stato ristabilito! Eppure, il nome di questa sezione risuona infausto… Se questa equazione è il coronamento della gloria di \( \pi \), come può anche essere il suo colpo di grazia?
3.1 Forme quadratiche
Esaminiamo questo modello perfetto di \( \pi \), \( A = \pi r^2 \). Notiamo che include il diametro—no, aspetta, il raggio—elevato alla seconda. Ciò lo rende una semplice forma quadratica. Queste forme si presentano in molti contesti; come fisico, i miei esempi preferiti provengono dal curriculum base di fisica. Ne prenderemo alcuni in considerazione.
Caduta in un campo gravitazionale
Galileo Galilei scoprì che la velocità di un oggetto che cade in un campo gravitazionale uniforme è proporzionale al suo tempo di caduta:
La costante di proporzionalità è l’accelerazione gravitazionale \( g \):
Dato che la velocità è la derivata della posizione, possiamo calcolare la distanza percorsa integrando:
Energia potenziale in una molla lineare
Robert Hooke scoprì che la forza esterna necessaria per allungare una molla è proporzionale allo spostamento:
La costante di proporzionalità è la costante elastica della molla \( k \):9
L’energia potenziale nella molla è dunque uguale al lavoro compiuto dalla forza esterna:
Energia cinetica
Isaac Newton scoprì che la forza su un oggetto è proporzionale alla sua accelerazione:
La costante di proporzionalità è la massa \( m \):
L’energia del moto, o energia cinetica, è uguale al lavoro compiuto per accelerare la massa alla velocità \( v \):
3.2 Un senso di presagio
Avendo già visto qualche esempio di semplici forme quadratiche in fisica, potreste avere ora un qualche presentimento. Come vedremo, è una sensazione perfettamente giustificata.

Come si vede in Figura 15, l’area del cerchio può essere calcolata dividendolo in corone circolari di lunghezza \( C \) e spessore \( dr \), dove l’area di ogni corona è \( C\,dr \):
A questo punto la circonferenza di un cerchio è proporzionale al suo raggio:
La costante di proporzionalità è \( \tau \):
L’area del cerchio è dunque l’integrale su tutti gli anelli:
Se eravate ancora dei difensori della causa di \( \pi \) all’inizio di questa sezione, ora siete rimasti a bocca aperta. Infatti, vediamo che anche in questo caso, dove presumibilmente \( \pi \) dovrebbe brillare, manca in realtà un fattore \( 2 \). Non a caso, la dimostrazione originale di Archimede non mostra che l’area di un cerchio è \( \pi r^2 \), ma che è uguale all’area di un triangolo rettangolo con base \( C \) e altezza \( r \). Applicando la formula per l’area triangolare otteniamo:
Semplicemente non c’è alcun modo per evitare quel fattore di \( 1/2 \) (Tabella 3).
| Quantità | Simbolo | Espressione |
| Distanza di caduta | \( y \) | \( \textstyle{\frac{1}{2}}gt^2 \) |
| Energia elastica | \( U \) | \( \textstyle{\frac{1}{2}}kx^2 \) |
| Energia cinetica | \( K \) | \( \textstyle{\frac{1}{2}}mv^2 \) |
| Area circolare | \( A \) | \( \textstyle{\frac{1}{2}}\tau\,r^2 \) |
Come volevasi dimostrare
Ci siamo posti in questo manifesto l’obiettivo di mostrare che \( \tau \) è la vera costante del cerchio. Dato che la formula per l’area del cerchio era proprio l’ultima, migliore argomentazione che \( \pi \) aveva ancora per sé, andrò fino in fondo dicendo: C.V.D.
4 Conflitto e resistenza
Nonostante la dimostrazione definitiva della superiorità di \( \tau \), molti continuano comunque ad opporsi sia alla notazione che al numero. In questa sezione, affrontiamo le preoccupazioni di coloro che accettano il valore ma non la lettera. Confutiamo poi alcune delle tante argomentazioni che si oppongono al rapporto \( C/r \) stesso, compreso il cosiddetto “Pi Manifesto” che difende il primato di \( \pi \). In questo contesto, discuteremo l’argomento relativamente avanzato del volume di una ipersefera (Sezione 5.1), che aumenta e amplifica le argomentazioni in Sezione 3 sull’area circolare.
4.1 Un giro
Il vero test di ogni notazione è il suo utilizzo; avendo visto l’uso di \( \tau \) per tutto questo manifesto, potreste già essere convinti che faccia il proprio dovere come simbolo. Ma per una costante così fondamentale come \( \tau \), sarebbe bello poter avere delle ragioni più profonde per questa nostra scelta. Perché non \( \alpha \), ad esempio, o \( \omega \)? Cosa rende \( \tau \) così speciale?
Ci sono due ragioni principali per usare \( \tau \) come costante del cerchio. La prima è che \( \tau \) assomiglia visivamente a \( \pi \): dopo secoli di utilizzo, l’associazione di \( \pi \) con la costante del cerchio è inevitabile, e l’utilizzo di \( \tau \) non fa che alimentare questa associazione invece di combatterla. (Effettivamente, la linea orizzontale nelle due lettere suggerisce l’interpretazione delle “gambe” come denominatori, dunque \( \pi \) ha due gambe nel denominatore, mentre \( \tau \) ne ha una sola. Visto in questo modo, il rapporto \( \tau = 2\pi \) è perfettamente naturale.)10
La seconda ragione è che \( \tau \) corrisponde a un giro di orologio (N.d.T.: in inglese, “turn”), e potreste aver notato che “\( \tau \)” e “turn” iniziano entrambi con il suono di una “t”. Questa è stata la motivazione originale per la scelta di \( \tau \), e non è una coincidenza: la radice della parola inglese “turn” è la parola di origine greca τόρνος (tornos), che significa “tornio”. Usando una font matematica per la prima lettera in τόρνος, otteniamo infine: \( \tau \).
Dal lancio originale de Il Tau Manifesto, ho appreso che Peter Harremoës propose indipendentemente l’uso di \( \tau \) all’autore di “\( \pi \) Is Wrong!” Bob Palais nel 2010, John Fisher propose \( \tau \) in un Usenet post nel 2004, e Joseph Lindenberg anticipò sia la proposta che il simbolo più di venti anni prima!11 Il Dr. Harremoës in particolare enfatizzò l’importanza di un’argomentazione inizialmente proposta in Sezione 1.1: usare \( \tau \) dà un nome alla costante del cerchio. Dato che \( \tau \) è una comune lettera greca, potrà essere pronunciata immediatamente anche da coloro che la incontreranno per la prima volta. Inoltre, diversamente dal chiamare la costante del cerchio semplicemente un “giro” (N.d.T.: in inglese, “a turn”), \( \tau \) funziona bene sia in contesti scritti che parlati. Ad esempio, dire che un quarto di cerchio rappresenta “un quarto di giro” radianti suona bene, ma “giro su quattro radianti” o “giro quarti radianti” suona scomodo, e “l’area di un cerchio è mezzo giro \( r \) al quadrato” suona decisamente strano. Usando \( \tau \), possiamo dire “tau quarti radianti” e “l’area di un cerchio è tau mezzi \( r \) al quadrato”.
Una notazione ambigua
Ovviamente, con ogni nuova notazione c’è la possibilità che vada in conflitto con l’uso attuale che se ne fa. Come notato in Sezione 1.1, “\( \pi \) Is Wrong!” evita questo problema introducendo un nuovo simbolo (Figura 3). Non è un caso isolato; ad esempio, negli albori della meccanica quantistica Max Planck introdusse la costante \( h \), che mette in relazione l’energia di un fotone con la sua frequenza (attraverso \( E = h\nu \)), ma i fisici presto realizzarono che è spesso più conveniente usare \( \hbar \) (letta “h tagliato”)—dove \( \hbar \) è semplicemente \( h \) diviso… umh… \( 2\pi \)—e quest’uso è ormai standard.
Ma far accettare un nuovo simbolo non è facile: gli deve essere dato un nome, quel nome deve essere reso popolare, e il simbolo stesso deve essere aggiunto ai sistemi di typesetting e ai word processor. Inoltre, promulgare un nuovo simbolo per \( 2\pi \) richiederebbe la cooperazione della comunità matematica accademica, che sul tema \( \pi \) vs. \( \tau \) è stata finora apatica nel migliore dei casi e ostile nel peggiore. Usare un simbolo già esistente ci permette di aggirare l’establishment matematico.12
Invece di sostenere un nuovo simbolo, il Tau Manifesto opta per l’uso di una lettera greca già esistente. Di conseguenza, dato che \( \tau \) è già usato in alcuni contesti, dobbiamo affrontare i conflitti con le pratiche esistenti. Fortunatamente ci sono davvero pochi usi comunemente adottati. Inoltre, mentre \( \tau \) è usato per certe variabili specifiche—e.g., sforzo di taglio in ingegneria meccanica, momento torcente in meccanica rotazionale, e tempo proprio in relatività generale e speciale—non c’è alcun utilizzo universale che sia in conflitto.13 In questi casi, possiamo o tollerare l’ambiguità oppure aggirare i pochi conflitti presenti cambiando caso per caso la notazione, come l’uso di \( N \) per il momento torcente14 o \( \tau_p \) for il tempo proprio.
Nonostante queste argomentazioni, i potenziali casi di conflitto nell’uso vero e proprio si sono dimostrati la maggior fonte di resistenza a \( \tau \). Alcuni hanno persino negato categoricamente che \( \tau \) (o, presumibilmente, qualsiasi altro simbolo al momento utilizzato) possa superare questi problemi. Ma gli scienziati e gli ingegneri hanno un’alta tolleranza per l’ambiguità notazionale, e dire che \( \tau \)-la-costante-del-cerchio non possa coesistere con altri utilizzi semplicemente ignora le varie dimostrazioni del contrario.
Un esempio di ambiguità facilmente tollerata si può ritrovare in meccanica quantistica, dove incontriamo la seguente formula per il raggio di Bohr, che (a grandi linee) è la “grandezza” di un atomo di idrogeno nel suo livello energetico più basso (lo stato fondamentale):
dove \( m \) è la massa di un elettrone ed \( e \) costituisce la sua carica. Al contempo, lo stato fondamentale stesso è descritto tramite una quantità conosciuta come la funzione d’onda, che decresce in modo esponenziale con un raggio su una scala di lunghezza dettata dal raggio di Bohr:
dove \( N \) è una costante di normalizzazione.
Avete già notato il problema? Probabilmente no, ed è proprio questo il punto. Il “problema” è che la \( e \) nel raggio di Bohr e la \( e \) nella funzione d’onda non sono la stessa \( e \)—la prima è la carica su un elettrone, mentre la seconda è il numero di Nepero (la base dei logaritmi naturali). Infatti, se espandiamo il fattore di \( a_0 \) nell’argomento dell’esponente nell’Eq. (10), otteniamo
che contiene una \( e \) elevata alla potenza di qualcosa con \( e \) di nuovo al suo interno. È ancora peggio di ciò che sembra, perché anche \( N \) stesso contiene \( e \):
Non ho alcun dubbio sul fatto che, se non fosse già esistita una notazione per il numero naturale, ogni proposta di usare la lettera \( e \) sarebbe stata considerata impossibile proprio a causa dei conflitti con altri usi. Eppure, in pratica nessuno ha mai avuto alcun tipo di problema nell’usare \( e \) nei contesti indicati sopra. Ci sono molti altri esempi, tra cui persino situazioni in cui \( \pi \) stesso è usato per due cose differenti.15 È difficile pensare come usare \( \tau \) per quantità differenti possa essere tanto diverso.
A tal proposito, i \( \pi \)-edanti là fuori (e si sono dimostrati essere molti) potranno notare che la funzione d’onda dello stato fondamentale dell’idrogeno ha un fattore di \( \pi \):
A prima vista, sembra essere più naturale della versione con \( \tau \):
Come al solito, le apparenze ingannano: il valore di \( N \) deriva dal prodotto
che mostra come la costante del cerchio entri in gioco tramite \( 1/\sqrt{2\pi} \), i.e., \( 1/\sqrt{\tau} \). Come per la formula per l’area del cerchio, la semplificazione che lascia un \( \pi \) a sé stante è una pura coincidenza.
4.2 Il Pi Manifesto
Nonostante molte obiezioni a \( \tau \) arrivino da corrispondenze email e commenti vari sparsi nel Web, c’è anche una resistenza organizzata. In particolare, dalla pubblicazione del Tau Manifesto nel giugno 2010, è apparso un “Pi Manifesto” per difendere la causa della tradizionale costante del cerchio. Questa sezione e le due successive contengono una confutazione di queste argomentazioni. Per necessità, questo sviluppo è più conciso ed avanzato rispetto al resto del manifesto, ma anche una lettura sommaria di quanto segue darà un’impressione della debolezza degli argomenti presentati dal Pi Manifesto.
Anche se possiamo certamente considerare l’apparizione del Pi Manifesto come un buon segno del continuo interesse per questo argomento, quest’ultimo fa diverse affermazioni false. Ad esempio, dice che il fattore di \( 2\pi \) nella distribuzione (normale) gaussiana è una coincidenza, e quest’ultima può essere scritta in modo più naturale come
Ma non è così: il fattore \( 2\pi \) deriva dall’elevare alla seconda la distribuzione gaussiana non normalizzata e passando in coordinate polari, il che porta a un fattore \( 1 \) dall’integrale radiale e a un fattore \( 2\pi \) dall’integrale angolare. Come per il caso dell’area circolare, il fattore \( \pi \) proviene da \( 1/2\times 2\pi \), non da \( \pi \) soltanto.
Un’affermazione correlata è il fatto che la funzione Gamma valutata in \( 1/2 \) sia più naturale in termini di \( \pi \):
dove
Ma \( \Gamma(\frac{1}{2}) \) si riduce allo stesso integrale gaussiano come per la distribuzione normale (ponendo \( u = x^{1/2} \)), dunque anche in questo caso il \( \pi \) è in realtà \( 1/2\times 2\pi \). Effettivamente, in molti dei casi citati del Pi Manifesto, la costante del cerchio entra in gioco con un integrale su tutti gli angoli, i.e., per \( \theta \) che va da \( 0 \) a \( \tau \).
Il Pi Manifesto esamina anche alcune formule per poligoni regolari a \( n \) lati (o “\( n \)-goni”). Ad esempio, fa notare che la somma degli angoli interni di un \( n \)-gono è data da
Questo problema è stato trattato in “Pi Is Wrong!”, che fa notare come: “La somma degli angoli interni [di un triangolo] è \( \pi \), certamente. Ma la somma degli angoli esterni di ogni poligono, da cui la somma degli angoli interni può essere facilmente derivata, e che viene generalizzata con l’integrale della curvatura di una curva chiusa semplice, è \( 2\pi \).” Inoltre, il Pi Manifesto offre la formula per l’area di un \( n \)-gono con raggio unitario (la distanza centro-vertice),
chiamandola “chiaramente… un’altra vittoria per \( \pi \).” Ma usando la formula di duplicazione \( \sin\theta\cos\theta = \frac{1}{2} \sin 2\theta \) vediamo che questa espressione può essere riscritta come
che è semplicemente
In altre parole, l’area di un \( n \)-gono ha un fattore naturale di \( 1/2 \). Infatti, facendo il limite dell’Eq. (12) per \( n\rightarrow \infty \) (e applicando la regola di L’Hôpital’s) otteniamo l’area di un poligono regolare unitario con infiniti lati, i.e., un cerchio unitario:
In questo contesto, dobbiamo notare come il Pi Manifesto faccia tanto rumore per nulla sul fatto che \( \pi \) sia l’area di un disco unitario, così da avere che (ad esempio) l’area di un quarto di cerchio (unitario) è \( \pi/4 \). Ciò sarebbe, come viene sostenuto, un’argomentazione altrettanto valida per \( \pi \) quanto la misura degli angoli in radianti lo è per \( \tau \). Sfortunatamente per questa osservazione, come notato nella Sezione 3 e come si vede ancora nell’Eq. (13), il fattore \( 1/2 \) sorge naturalmente nel contesto dell’area circolare. Infatti, la formula per l’area di un settore circolare sotteso da un angolo \( \theta \) è
quindi non c’è alcun modo di evitare il fattore \( 1/2 \) in generale. (Vediamo dunque che \( A = \frac{1}{2} \tau\, r^2 \) è semplicemente il caso speciale \( \theta = \tau \).)
In breve, la differenza fra la misurazione degli angoli e l’area non è arbitraria. Non c’è alcun fattore naturale di \( 1/2 \) nel caso della misurazione degli angoli. Al contrario, nel caso dell’area il fattore di \( 1/2 \) sorge attraverso l’integrale di una funzione lineare in associazione con una semplice forma quadratica. In realtà, le argomentazioni per \( \pi \) sono persino peggiori di quanto sembrino, come mostrato nella prossima sezione.
5 Andando al fondo della questione di pi e tau
Continuo a restare impressionato da quanto sia ricco questo argomento, e la mia comprensione di \( \pi \) e \( \tau \) continua anch’essa ad evolvere. Nell’Half Tau Day, 2012, credevo di aver identificato esattamente cosa ci fosse di sbagliato in \( \pi \). La mia argomentazione si basava su un’analisi dell’area superficiale e del volume di una sfera \( n \)-dimensionale, che (come mostrato sotto) rende chiaro che \( \pi \) non possiede nessun significato geometrico fondamentale. Tuttavia, la mia analisi era incompleta—un fatto a cui sono venuto a conoscenza grazie a un notevole messaggio del lettore del Tau Manifesto Jeff Cornell. Di conseguenza, questa sezione è un tentativo non solo di sfatare definitivamente \( \pi \), ma anche di articolare la verità su \( \tau \), una verità molto più profonda e sottile di quanto immaginassi.
Nota: Questa sezione è più avanzata rispetto al resto del manifesto e può essere saltata senza perdità di continuità. Se la doveste trovare confusa, vi consiglierei di procedere direttamente alla conclusione nella Sezione 6.
5.1 Area e volume di una ipersfera
Iniziamo le nostre indagini con la generalizzazione di un cerchio a dimensioni arbitrarie.16 Questo oggetto, chiamato ipersfera o \( n \)-sfera, può essere definito come segue.17 (Per comodità, si assume che queste sfere siano centrate nell’origine.) Una \( 0 \)-sfera è l’insieme vuoto, e definiamo la sua “parte interna” come un punto.18 Una \( 1 \)-sfera è l’insieme di tutti i punti che soddisfano
che consiste nei due punti \( \pm r \). La sua parte interna, che soddisfa
è il segmento da \( -r \) a \( r \). Una \( 2 \)-sfera è un cerchio, ovvero l’insieme di tutti i punti che soddisfano
La sua parte interna, che soddisfa
è un disco. Allo stesso modo, una \( 3 \)-sfera soddisfa
e la sua parte interna è una palla. La generalizzazione a \( n \) arbitrari, sebbene difficile da visualizzare per \( n > 3 \), è immediata: una \( n \)-sfera è l’insieme di tutti i punti che soddisfano
Il Pi Manifesto (discusso in Sezione 4.2) include una formula per il volume di una \( n \)-sfera unitaria come argomentazione in favore di \( \pi \):
dove la funzione Gamma è data dall’Eq. (11). L’Eq. (14) è un caso speciale della formula per un raggio generico, ed è anch’essa tipicamente scritta in termini di \( \pi \):
Poiché \( V_n(r) = \int S_n(r)\,dr \), abbiamo \( S_n(r) = dV_n(r)/dr \), il che significa che l’area può essere scritta in questo modo:
Invece di considerare queste formule direttamente, vediamo se possiamo in qualche modo districarle per fare più luce sulla questione di \( \pi \) vs. \( \tau \). Iniziamo la nostra analisi osservando che l’apparente semplicità delle formule sopra indicate è un’illusione: sebbene la funzione Gamma sia notazionalmente semplice, in realtà è un integrale su un dominio semi-infinito, il che non è affatto un’idea banale. Fortunatamente, la funzione Gamma può essere semplificata in alcuni casi particolari. Per esempio, quando \( n \) è un intero, è facile mostrare (usando integrazione per parti) che
Vista in questo modo, \( \Gamma \) può essere interpretata come una generalizzazione della funzione fattoriale ad argomenti di valore reale.19
Nelle formule per area e volume \( n \)-dimensionali, l’argomento di \( \Gamma \) non è necessariamente un intero, ma è piuttosto \( \left(1 + \frac{n}{2}\right) \), che è un intero quando \( n \) è pari ed è metà-intero quando \( n \) è dispari. Tenendo conto di questo fatto otteniamo la seguente espressione, che è presa da un riferimento standard, Wolfram MathWorld, ed è come solito espressa in termini di \( \pi \):
Integrando rispetto ad \( r \) otteniamo
Esaminiamo l’Eq. (18) più in dettaglio. Notiamo innanzitutto che MathWorld usa la funzione doppio fattoriale \( n!! \)—ma, stranamente, viene usato solo nel caso dispari. (Questo è un indizio di ciò che ci aspetta.) La funzione doppio fattoriale, anche se incontrata raramente in matematica, è elementare: è come la normale funzione fattoriale, ma sottrae \( 2 \) di volta in volta invece che \( 1 \), così che, e.g., \( 5!! = 5 \cdot 3 \cdot 1 \) e \( 6!! = 6 \cdot 4 \cdot 2 \). In generale, abbiamo
(Per definizione, \( 0!! = 1!! = 1 \).) Possiamo notare come l’Eq. (19) si divida naturalmente in casi pari e dispari, rendendo la decisione di MathWorld di usarla solo nel caso dispari ancora più misteriosa.
Per risolvere questo mistero, inizieremo dando un’occhiata più da vicino alla formula per \( n \) dispari nell’Eq. (18):
Esaminando l’espressione
notiamo che può essere riscritta come
e qui riconosciamo il nostro vecchio amico \( 2\pi \).
Consideriamo ora il caso pari nell’Eq. (18). Abbiamo fatto notare sopra quanto sia strano usare il fattoriale ordinario nel caso pari ma il doppio fattoriale nel caso dispari. In effetti, dato che il doppio fattoriale è già definito per casi, possiamo unificare le formule usando \( n!! \) in entrambi i casi e metterlo così a fattor comune:
Dunque, c’è qualche relazione tra il fattoriale e il doppio fattoriale? Sì—quando \( n \) è pari, i due sono correlati dalla seguente identità:
(Questa proprietà è facile da verificare per induzione matematica.) Sostituendo questa espressione nella formula per il volume quando \( n \) è pari otteniamo
che ha una sorprendente somiglianza con
e ancora una volta troviamo un fattore di \( 2\pi \).
Mettendo insieme questi risultati, vediamo che l’Eq. (18) può essere riscritta come
e l’Eq. (17) può essere riscritta come
Applicando la sostituzione \( \tau=2\pi \) nell’Eq. (21) otteniamo
Per unificare ulteriormente le formule, possiamo usare la funzione parte intera \( \lfloor x \rfloor \), che semplicemente esprime l’intero più grande minore o uguale ad \( x \) (equivalente a tagliare via la parte frazionaria, così da avere, e.g., \( \lfloor 3.7 \rfloor = \lfloor 3.2 \rfloor = 3 \)). Con questo abbiamo che
il che ci permette di scrivere la formula in questo modo:
Integrando l’Eq. (22) rispetto ad \( r \), otteniamo infine
Lambda
Le formule nelle Eq. (22) e Eq. (23) rappresentano un notevole miglioramento rispetto alle formulazioni originali (Eq. (17) e Eq. (18)) in termini di \( \pi \). Ma in realtà è possibile un’ulteriore semplificazione, utilizzando la misura di un angolo retto:20
Come vedremo nella Sezione 5.2, l’Eq. (24) può essere riscritta in modo più naturale in termini delle simmetrie del cerchio:
dove il fattore \( 2^2 \) deriva dai \( 2^2 \) archi circolari congruenti (uno in ogni quadrante) nello spazio bidimensionale.
Il maggior vantaggio di \( \lambda \) è che unifica completamente i casi pari e dispari nelle Eq. (22) e Eq. (23), che posseggono entrambe un fattore \( \tau^{\left\lfloor \frac{n}{2} \right\rfloor} \). Applicando la sostituzione espressa dall’Eq. (25) otteniamo
Possiamo dunque riscrivere il prodotto
come
il che elimina la dipendenza esplicita sulla parità. Applicando l’Eq. (26) alle Eq. (22) e Eq. (23) otteniamo
e
Questa semplificazione nelle Eq. (27) e Eq. (28) sembra avvenire al costo di un fattore \( 2^n \), ma persino questo ha un chiaro significato geometrico: una sfera in \( n \) dimnsioni si divide naturalmente in \( 2^n \) parti congruenti, corrispondendo così alle \( 2^n \) famiglie di soluzioni di \( \sum_{i=1}^{n} x_i^2 = r^2 \) (una per ogni scelta di \( \pm x_i \)). In due dimensioni, queste rappresentano gli archi circolari in ognuno dei quattro quadranti; in tre dimensioni, rappresentano i settori della sfera in ogni ottante; e così via con l’aumentare delle dimensioni. In altre parole, possiamo sfruttare la simmetria della sfera calcolando l’area o il volume di una parte—tipicamente la parte principale con \( x_i > 0 \) per ogni \( i \)—per poi trovare il valore totale moltiplicando per \( 2^n \).
Che io sappia, le Eq. (27) e Eq. (28) sono le formulazioni più semplici possibili per le formule dell’area e del volume sferico (ed effettivamente le uniche forme che sono stato in grado di memorizzare con costanza). Consideriamo in particolare quella per il volume: a differenza dell’apparente semplicità dell’Eq. (15), l’Eq. (28) non utilizza nessun integrale particolare—solo le leggermente esotiche, ma comunque elementari, funzioni parte intera e doppio fattoriale. Il volume di una \( n \)-sfera unitaria è semplicemente il volume di ogni parte simmetrica, \( \lambda^{\left\lfloor \frac{n}{2} \right\rfloor}/n!! \), moltiplicata per il numero di parti, \( 2^n \).
Ricorrenze
Abbiamo visto, tramite le Eq. (27) e Eq. (28), che le formule per l’area e il volume sono più semplicemente espresse in termini dell’angolo retto \( \lambda \). Tuttavia, non abbiamo ancora finito con \( \tau \).
Come notato nell’Eq. (28), la formula per il volume si divide in modo naturale in due famiglie, corrispondenti agli spazi dimensionali pari e dispari, rispettivamente. Ciò significa che il volume quadridimensionale, \( V_4 \), è collegato semplicemente a \( V_2 \) ma non a \( V_3 \), mentre \( V_3 \) è collegato a \( V_1 \) ma non a \( V_2 \). In che modo sono allora esattamente connessi?
Possiamo trovare la risposta derivando le relazioni di ricorrenza tra dimensioni.21 In particolare, dividiamo il volume di una sfera \( n \)-dimensionale per il volume di una sfera \( (n-2) \)-dimensionale:
Vediamo dall’Eq. (29) che possiamo ottenere il volume di una \( n \)-sfera semplicemente moltiplicando la formula per una \( (n-2) \)-sfera per \( r^2 \) (un fattore richiesto per analisi dimensionale), dividendo per \( n \), e moltiplicando per la “costante di ricorrenza” \( 2^2\lambda \).
Allo stesso modo, per la superficie abbiamo che
con la stessa costante di ricorrenza \( 2^2\lambda \).
Dunque, sia nell’Eq. (29) che Eq. (30), la costante che mette in relazione le due dimensioni non è \( \lambda \) per sé, ma la combinazione \( 2^2\lambda \). Mettendola a confronto con l’Eq. (25), vediamo che questa non è nient’altro che \( \tau \)! Infatti, una derivazione alternativa per calcolo diretto della relazione di ricorrenza per il volume (che utilizza \( R \) dove noi scriviamo \( r \)) conclude con l’integrale
mostrando così che l’identificare \( \tau \) come la “costante di ricorrenza” non è una coincidenza—la costante di ricorrenza e la costante del cerchio sono in realtà proprio la stessa cosa:
Di conseguenza, è \( \tau \), non \( \lambda \), a fornire il filo conduttore che unisce le due famiglie di soluzioni pari e dispari, come illustrato da Joseph Lindenberg in Tau Before It Was Cool (Figura 16).22
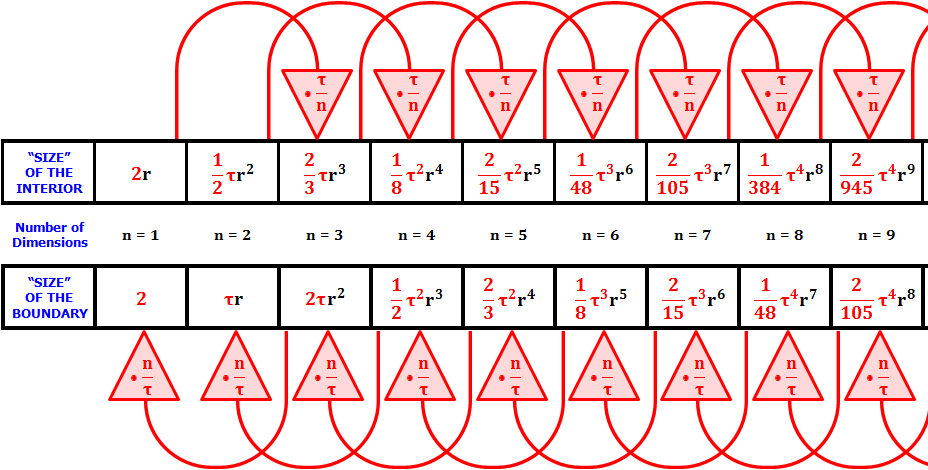
Nel contesto generale di sfere \( n \)-dimensionali, indicheremo per comodità le formule per l’area e il volume in termini di \( \lambda \) come per le Eq. (27) e Eq. (28), ma dato un \( n \) qualsiasi esprimeremo i risultati in termini della costante di ricorrenza \( \tau \).
5.2 Tre famiglie di costanti
Armati con gli strumenti sviluppati nella Sezione 5.1, siamo ora pronti ad andare al fondo della questione di \( \pi \) e \( \tau \). Per completare l’immersione, useremo l’Eq. (27) e Eq. (28) per definire due famiglie di costanti, e poi usare le definizioni di \( \pi \) (Eq. (1)) per definirne una terza e rivelare esattamente cosa c’è di sbagliato in \( \pi \).
In primo luogo, definiamo una famiglia di “costanti superficiali” \( \tau_n \) dividendo l’Eq. (27) per \( r^{n-1} \), la potenza di \( r \) necessaria per ottenere una costante adimensionale:
In secondo luogo, definiamo una famiglia di “costanti volumetriche” \( \sigma_n \) dividendo la formula per il volume Eq. (28) per \( r^n \):
Con le due famiglie di costanti definite nelle Eq. (32) e Eq. (33), possiamo scrivere le due formule per l’area e il volume (Eq. (27) e Eq. (28)) in modo compatto come segue:
e
Grazie al fatto che \( V_n(r) = \int S_n(r)\,dr \), abbiamo la semplice relazione
Facciamo alcune osservazioni su queste due famiglie di costanti. La famiglia \( \tau_n \) ha un importante significato geometrico: ponendo \( r=1 \) nell’Eq. (32), notiamo che ogni \( \tau_n \) è l’area di una \( n \)-sfera unitaria, che è anche la misura angolare di una \( n \)-sfera completa. In particolare, indicando con \( s_n(r) \) la “lunghezza d’arco” \( n \)-dimensionale pari a una frazione \( f \) dell’area totale \( S_n(r) \), abbiamo
Qui \( \theta_n \) è semplicemente la generalizzazione \( n \)-dimensionale della misura angolare in radianti, e vediamo che \( \tau_n \) è la generalizzazione di “un giro” a \( n \) dimensioni, il che spiega perché la costante della 2-sfera (del cerchio) \( \tau_2 = 2^2\lambda = \tau \) porta così naturalmente al diagramma mostrato in Figura 10. Inoltre, abbiamo imparato nella Sezione 5.1 che \( \tau_2 \) è anche la “costante di ricorrenza” per aree e volumi della \( n \)-sfera.
Analogamente, le \( \sigma_n \) sono i volumi delle \( n \)-sfere unitarie. In particolare, \( \sigma_2 \) è l’area di un disco unitario:
Ciò mostra che \( \sigma_2 = \tau/2 = 3.14159\ldots \) ha effettivamente un significato geometrico indipendente. È importante notare, tuttavia, che non ha niente a che fare con diametri né circonferenze. In altre parole, \( \pi = C/D \) non è un membro della famiglia \( \sigma_n \).
Dunque, a quale famiglia di costanti appartiene in modo naturale \( \pi \)? Riscriviamo l’Eq. (1) in termini più appropriati per generalizzare a dimensioni superiori:
Vediamo dunque che \( \pi \) è naturalmente associato con aree divise dalla potenza del diametro necessaria per ottenere una costante adimensionale. Il che suggerisce l’introduzione di una terza famiglia di costanti \( \pi_n \):
Possiamo esprimere questa equazione in termini della famiglia \( \tau_n \) sostituendo \( D = 2r \) nell’Eq. (34) e applicando l’Eq. (32):
Ora siamo finalmente in grado di capire esattamente cosa c’è di sbagliato in \( \pi \). La principale significatività geometrica di \( 3.14159\ldots \) è che è l’area di un disco unitario. Ma questo numero deriva dal calcolare \( \sigma_n = \tau_n/n \) quando \( n=2 \):
Effettivamente è uguale a \( \pi_2 \):
Ma questa uguaglianza è una coincidenza: accade solo perché \( 2^{n-1} \) è accidentalmente uguale a \( n \) se \( n=2 \) (ovvero, \( 2^{2-1} = 2 \)). In tutte le dimensioni superiori, \( n \) e \( 2^{n-1} \) sono distinti. In altre parole, il significato geometrico di \( \pi \) è il risultato di un gioco di parole matematico.
6 Conclusione
Nel corso degli anni, ho sentito molte argomentazioni contro il fatto che \( \pi \) sia “sbagliato” e contro la correttezza di \( \tau \), quindi prima di concludere la nostra discussione permettetemi di provare a rispondere ad alcune delle domande più frequenti.
6.1 Domande frequenti
- Dici sul serio? Ovviamente. Voglio dire, mi sto un po’ divertendo con questi argomenti, e il tono è occasionalmente leggero, ma c’è uno scopo serio. Porre la costante del cerchio uguale al rapporto fra circonferenza e diametro è una convenzione scomoda e che confonde. Anche se mi piacerebbe tanto vedere i matematici cambiare le proprie abitudini, non sono particolarmente preoccupato per loro; sanno badare a se stessi. La mia preoccupazione è per i neofiti, perché sono loro a subire il danno maggiore di questa scelta: come notato in Sezione 2.1, \( \pi \) è un disastro pedagogico. Provate a spiegare a un dodicenne (o a un trentenne) perché l’angolo espresso da un ottavo di cerchio—una fetta di pizza—è \( \pi/8 \). Un attimo, volevo dire \( \pi/4 \). Capite cosa intendo? È una follia—una pura e semplice follia.
- Come possiamo passare da \( \pi \) a \( \tau \)? La prossima volta che scriverete qualcosa che utilizza la costante del cerchio, dite semplicemente “Per comodità, sia \( \tau = 2\pi \)”, per poi procedere come al solito. (Ovviamente, questo potrebbe far sorgere la domanda a qualcuno, “Perché mai dovresti volerlo fare?”, e ammetto che sarebbe bello poter avere un posto a cui poterli rimandare. Se solo qualcuno scrivesse, diciamo, un manifesto a riguardo…) Il modo per far sì che le persone inizino ad usare \( \tau \) è iniziare ad usarlo noi stessi.
- Non è troppo tardi per cambiare? Non dovrebbero essere riscritti tutti i libri e le pubblicazioni? No in entrambi i casi. È vero che alcune convenzioni, anche se sfortunate, sono effettivamente irreversibili. Ad esempio, la scelta di Benjamin Franklin per i segni delle cariche elettriche fa sì che il familiare esempio delle correnti elettriche (ovvero, gli elettroni liberi nei metalli) le ponga come positive quando i portatori di carica sono negativi, e viceversa—maledicendo da allora gli studenti di fisica con la confusione dei segni negativi.23 Cambiare questa convenzione vorrebbe davvero dire riscrivere tutti i libri di testo (e bruciare quelli vecchi) dato che è impossibile dire a colpo d’occhio quale convenzione viene usata. Al contrario, mentre la ridefinizione di \( \pi \) è di fatto impossibile, possiamo passare da \( \pi \) a \( \tau \) al volo usando la conversione
\[ \pi \leftrightarrow \textstyle{\frac{1}{2}}\tau. \]
È semplicemente una questione di sostituzione matematica, completamente robusta e reversibile fino in fondo. Il passaggio da \( \pi \) a \( \tau \) può avvenire quindi in modo incrementale; a differenza di una ridefinizione, non è necessario che avvenga tutta d’un tratto.
- L’uso di \( \tau \) non rischia di confondere, gli studenti specialmente? Se siete abbastanza intelligenti da capire la misurazione degli angoli in radianti, siete abbastanza intelligenti da capire \( \tau \)—e anche perché \( \tau \) confonde in realtà meno di \( \pi \). Oltretutto, non c’è nulla che rischia intrinsecamente di confondere nel dire “Sia \( \tau = 2\pi \)”; in senso stretto, è solo una semplice sostituzione. Infine, possiamo sfruttare la situazione come un’opportunità didattica: l’idea che \( \pi \) possa essere sbagliato è interessante, e gli studenti possono interagire con il materiale convertendo le equazioni nei loro libri di testo da \( \pi \) a \( \tau \) per vedere con i propri occhi quale delle due scelte è la migliore.
- Tutto ciò ha davvero importanza? Certamente. La costante del cerchio è importante. Le persone ci tengono abbastanza da scrivere interi libri sull’argomento, da celebrarla ogni anno in un giorno particolare, e da memorizzarne decine di migliaia di cifre. Per me è abbastanza importante da scriverne un intero manifesto, e per te forse abbastanza da leggerlo. E proprio perché è importante è difficile ammettere che la convenzione al momento in uso è sbagliata. (Voglio dire, come si fa ad andare a dirglielo a Rajveer Meena, detentore del record mondiale, che ha appena recitato 70,000 cifre decimali di metà della vera costante del cerchio?) Dato che la costante del cerchio è importante, è importante sceglierla correttamente, e abbiamo visto in questo manifesto che la costante corretta è \( \tau \). Anche se \( \pi \) è di grande importanza storica, l’importanza matematica di \( \pi \) è che è metà \( \tau \).
- Come mai è stato \( \pi \) ad essere utilizzato per primo? Come notazione, \( \pi \) venne reso popolare circa 300 anni fa da Eulero (basandosi su lavori di William Jones), ma le origini di \( \pi \)-il-numero si perdono nella notte dei tempi. Sospetto che la convenzione di usare \( C/D \) invece di \( C/r \) nacque semplicemente perché è più semplice misurare il diametro di un oggetto circolare rispetto al misurare il raggio. Ma questo non lo rende buona matematica, e mi sorprende che Archimede, che ha notoriamente approssimato la costante del cerchio, non si sia reso conto che \( C/r \) è il numero più fondamentale. Ma sono ancora più sorpreso che Eulero non abbia corretto il problema quando ne ha avuto la possibilità; a differenza di Archimede, Eulero aveva il vantaggio della notazione algebrica moderna, che (come abbiamo visto a partire dalla Sezione 2.1) rende abbondantemente chiare le relazioni sottostanti tra il cerchio e la sua costante. Incredibilmente, Eulero stesso usò il simbolo \( \pi \) per indicare sia \( C/D \) che \( C/r \) in due momenti diversi! Un vero peccato che non abbia standardizzato la scelta più conveniente.
- Perché ti interessa questo argomento? Prima di tutto, come cercatore di verità mi interessa la correttezza delle spiegazioni. Secondo, come insegnante ci tengo alla chiarezza nell’esposizione. Terzo, come hacker adoro questi "trucchetti" (N.d.T.: in inglese, "hack"). Quarto, come studente della storia e della natura umana trovo affascinante come l’assurdità di \( \pi \) sia rimasta in bella vista per secoli prima che qualcuno se ne accorgesse. Inoltre, molte delle persone che hanno mancato il bersaglio della vera costante del cerchio erano tra le persone più razionali e intelligenti che siano mai vissute. Quali altre cose ci stanno guardando in faccia in questo momento, in attesa soltanto di essere scoperte?
- Sei forse una specie di pazzo? Non sono proprio affari vostri, ma no. Oltre all’indossare occasionalmente scarpe insolite, sono normale sotto ogni altro aspetto. Non indovinereste mai che, lungi dall’essere un comune cittadino, sono in realtà un famigerato propagandista matematico.
- E i giochi di parole con \( \pi \)? Arriviamo ora all’obiezione finale. Lo so, lo so, “\( \pi \) in the sky” è una battuta così simpatica. Eppure, anche \( \tau \) è pieno di possibilità. Il \( \tau \)ismo ci dice: non è \( \tau \) ad essere una parte di \( \pi \), (N.d.T.: "a piece of \( \pi \)") ma \( \pi \) ad essere una parte di \( \tau \)—metà \( \tau \), per essere esatti. L’identità \( e^{i\tau} = 1 \) dice: “Sii uno con il \( \tau \).” E anche se l’osservazione che “Una rotazione di un giro è 1” può sembrare una \( \tau \)-tologia, è la vera natura del \( \tau \). Mentre contempliamo questa natura per ricercare la via del \( \tau \), dobbiamo ricordarci che il \( \tau \)ismo è basato sulla ragione, non sulla fede: i \( \tau \)isti non sono mai persone \( \pi \)e.
6.2 Sii uno con il tau
Abbiamo visto ne Il Tau Manifesto che la scelta naturale per la costante del cerchio è il rapporto non tra la circonferenza di un cerchio e il suo diametro, ma il suo raggio. Questo numero necessita di un nome, e spero che possiate unirvi a me nel chiamarlo \( \tau \):
Il suo uso è naturale, la motivazione chiara, e le implicazioni profonde. Inoltre, porta con sé un bellissimo diagramma (Figura 17). Vediamo in Figura 17 un movimento attraverso lo yang (“la luce, il bianco, il movimento verso l’alto”) verso \( \tau/2 \) e un ritorno con lo yin (“il buio, il nero, il movimento verso il basso”) di nuovo a \( \tau \).24 Usare \( \pi \) al posto di \( \tau \) è come avere lo yang senza lo yin.

6.3 Il Tau Day
Il Tau Manifesto è stato lanciato per la prima volta nel Tau Day: 28 giugno (6/28), 2010. Il Giorno del Tau è un momento per celebrare e gioire di tutto ciò che è matematico.25 Se desiderate ricevere aggiornamenti su \( \tau \), tra cui notifiche su possibili eventi nei futuri Tau Day, potete iscrivervi alla Tau Manifesto mailing list qui sotto. E se pensate che i rotondeggianti dolci cucinati nella Giornata del Pi siano particolarmente gustosi, aspettate—la Giornata del Tau ha il doppio della torta! (N.d.T.: Tau Day has twice as much pi(e)!)
Share the τ Manifesto
Ringraziamenti
Vorrei innanzitutto ringraziare Bob Palais per aver scritto “\( \pi \) Is Wrong!”. Non ricordo quanto fossero profondi i miei sospetti su \( \pi \) prima di incontrare quell’articolo, ma “\( \pi \) Is Wrong!” mi ha sicuramente aperto gli occhi, e ogni sezione de Il Tau Manifesto ha nei suoi confronti un debito di gratitudine. Vorrei anche ringraziare Bob per i suoi utili commenti a questo manifesto, e soprattutto per essere stato così incoraggiante al riguardo.
È da un po’ di tempo che penso al Tau Manifesto, e molte delle idee qui presentate sono state sviluppate attraverso le numerose conversazioni con il mio amico Sumit Daftuar. Sumit ha fatto da cassa di risonanza e occasionalmente da avvocato del diavolo, e la sua intuizione come insegnante e come matematico ha influenzato il mio pensiero in molti modi.
Ho anche ricevuto incoraggiamenti e feedback utili da diversi lettori. Vorrei ringraziare Vi Hart e Michael Blake per i loro incredibili video ispirati a \( \tau \), così come Don “Blue” McConnell e Skona Brittain per aver contribuito a rendere \( \tau \) parte della geek culture (tramite l’app per iPhone time-in-\( \tau \) e il tau clock, rispettivamente). La piacevole interpretazione del simbolo yin-yang usato nel The Tau Manifesto è grazie a un suggerimento di Peter Harremoës, che (come detto precedentemente) ha la rara distinzione di aver proposto in modo indipendente l’uso di \( \tau \) per la costante del cerchio. Un altro tauista pre–Tau Manifesto, Joseph Lindenberg, è da sempre stato anch’egli un fedele sostenitore, e il suo entusiasmo è molto apprezzato. Ho ricevuto diversi utili suggerimenti da Christopher Olah, in particolare riguardo all’interpretazione geometrica dell’identità di Eulero, e la Sezione 2.3.2 sulle identità euleriane è stata inspirata da un’eccellente indicazione di Timothy “Patashu” Stiles. Don Blaheta ha anticipato e ispirato parte del materiale sulle ipersfere, e John Kodegadulo li ha messi insieme in modo particolarmente chiaro e divertente. Poi Jeff Cornell, con la sua osservazione sull’importanza di \( \tau/4 \) in questo contesto, ha scosso la mia fede e mi ha lasciato a bocca aperta.
Infine, vorrei ringraziare Wyatt Greene per il suo feedback straordinariamente utile su una bozza pre-pubblicazione del manifesto; tra le altre cose, se doveste mai aver bisogno di qualcuno che vi dica che “praticamente quasi tutta la [ora cancellata] sezione 5 è spazzatura”, Wyatt è il vostro uomo.
Copyright
Il Tau Manifesto. Copyright © 2010–2018, Michael Hartl.

