1 圆周率
数学里有很多重要的数字。这篇《Tau 宣言》献给的是其中一个或许也是最为重要的一个数字:圆周率。圆周率描述的是圆的周长和它的线性尺度之间的关系。千百年以来,圆形一直被人们认为是最完美的几何图形,而圆周率这一个数就完美概括了圆形的全部几何内涵。我们知道一直以来圆周率都是用 \( \pi \) 来表示的。但是,数学家 Bob Palais 曾经对此发表过一篇赏心悦目的文章,题目叫 《\( \pi \) 是错误的!》1。正如文章题目所言,他认为 \( \pi \) 是错误的。现在是到了纠正这个错误的时候了。
1.1 一个自负的提议
要想弥补这个过失,我们首先要来了解一下 \( \pi \) 这个数字的来历。\( \pi \) 的传统定义是圆的周长(C)和其直径(D)的比率2:
\( \pi \) 这个数字有很多非同寻常的特性,其中最为突出的一个特性是,它既是一个无理数又是一个超越数。它在各种数学公式里也经常出现。
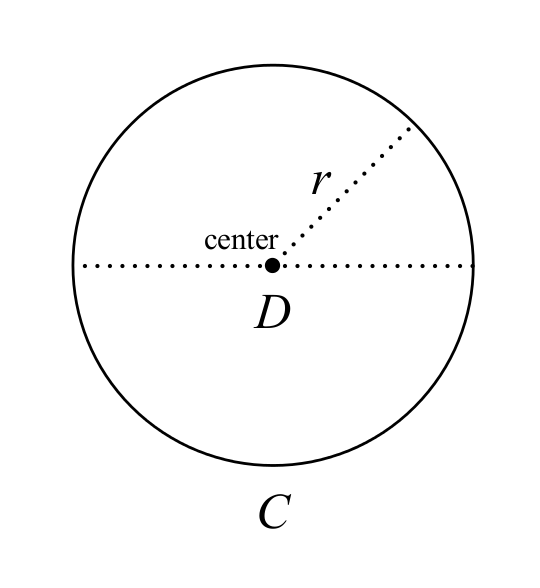
\( \pi \) 作为一个数字当然并没有“错”。\( \pi \) 有明确的定义,而且具有数学家赋予它的所有属性。我们说“\( \pi \) 是错误的”, 其实是想指出用 \( \pi \) 作为圆周率不但给我们带来很多困扰而且也是一个非常不自然的选择。圆的定义是在离某一个指定的点(圆心)等距(半径)的地方用一系列的点连成的图形(图1)。各个方向都等宽的几何图形有无限多种3(图2),但是其中只有一种图形在各个方向上都有一样的半径,那就是圆形。这也说明了为什么用半径 \( r \) 来定义圆周率比用直径 \( D \) 更为自然:
因为直径是半径的两倍,所以圆周率也应该是 \( \pi \) 的两倍:\( 2\pi \)。和 \( \pi \) 一样,真正的圆周率 \( 2\pi \) 也是超越数和无理数,而且它也同样经常出现在各种数学公式里(我们将在第 2 节举一些例子)。
在《\( \pi \) 是错误的!》那篇文章中 Bob Palais 用令人信服的论证说明了为什么他偏向用 \( 2\pi \) 作为圆周率。我认为他是提出并普及这个议题的首要发起人。他把这个圆周率直观的叫做“一周”,同时还引入了一个新的数学符号来表示它(图3)。接下来我们会看到虽然他对圆周率的描述是很有先见之明的,但是他引入的那个符号有些怪异(在第 4 节我们会继续讨论),所以要想获得广泛的采纳似乎希望渺茫。

《Tau 宣言》所要表达的立场是:对于“\( \pi \) 是错误的”这一观点,我们正确的回应应该是“的确如此”。真正的圆周率应该拥有一个合理的名称和符号。现在你一定也猜出来了,《Tau 宣言》提议用希腊字母 \( \tau \) (tau) 来作为圆周率的名称和符号:
在接下来的部分里,我们可以看到数字 \( \tau \) 才是圆周率的正确选择。而且我们也会通过实际应用和直接论证(参见第 2节和第 3 节)来说明为什么字母 \( \tau \) 也是一个很自然的圆周率的名称和符号选择。
1.2 一个强劲的对手
在我们开始证明为什么 \( \tau \) 是圆周率的自然选择之前,我们先来认识一下我们要挑战的这个强劲对手。经过几百年的宣传和推广,\( \pi \) 的使用已经深入人心。人们写了一本又一本的书来颂扬 \( \pi \) 的优点,其数量之多可谓汗牛充栋(例如 The Joy of Pi, Pi in the Sky, A History of Pi, Pi: A Source Book 等等)。而且对 \( \pi \) 非理性的崇拜甚至已经扩散到了极客世界的最高领域。比如,谷歌(Google)在 2010 年 3 月 14 日(Pi Day)的时候把他们的主页图标改成了图4的样子,以表达对 \( \pi \) 的敬意。
同时也有很多人可以背诵这一神秘数字的几十位,几百位,甚至 几千位数。 像下面这位只能记住 \( \pi \) 前 40 位数的人只能算小儿科了4(图5)。
所以说,\( \tau \) 的支持者面对的是一个强劲的对手。但是我们有一个更强大的同盟,因为真理站在我们这边。
2 数字 Tau
我们在第 1.1 节里提到 \( \tau \) 也可以写成 \( 2\pi \)。正如文章《\( \pi \) 是错误的!》所说的,单是注意到 \( 2\pi \) 在数学公式里频繁出现这个现象就能激起人们对这一课题的极大兴趣。比如在极坐标系里对全空间的积分:
\( \theta \) 积分的上限总是 \( 2\pi \)。这个因子同样出现在高斯(正态)分布的定义里,
还有傅里叶变换公式,
第 \( n \) 项单位根公式,
以上这些公式并非特别挑选出来的,你只需要打开你最喜欢的物理或数学书自己找找看,这样的例子实在太多了,这也意味着 \( 2\pi \) 这个因子是有一定的特殊性的。
为了寻找这一神秘现象的根源,我们必须从圆的基本属性出发,特别是从角度这一概念的基本属性出发来展开讨论。尽管你可能对这些概念和内容都很熟悉,但是还是值得在此重新回顾一下,并从这里开始对 \( \tau \) 有真正的理解。
2.1 圆和角
圆和角这两个概念之间的关系是很密切的。在图6中我们可以看到,这两个同心圆有不同长度的半径。形成 \( \theta \) 角的两条半径线在两个同心圆上截取了不同长度的圆弧,但是它们对应的 \( \theta \) 角却是相同的。也就是说,角度的大小和决定圆弧的半径长度无关。角度测度体系的首要任务就是要抓住角度和半径无关这一特性。

我们通常用度数来定义和测量角的大小,也就是把一个圆分成 360 等分。在这个测度体系里,如图7所示,有一些角度是比较特殊的(熟悉三角函数的学生都知道)

但是我们知道数学里还有一个更为基本的用弧长 \( s \) 和半径 \( r \) 来表示角的测度体系。在图6中,尽管半径线在不同的圆上截取的弧长不同,但是弧长和半径的变化是成正比的,所以弧长和半径的比率在以上两个情况下相等:
这便导出了弧度的定义和测度体系:
这一定义体现了角的大小和半径无关的特性。而且因为弧长 \( s \) 和半径 \( r \) 都有一样的长度单位,所以弧度是无量纲的。弧度体系让数学里很多公式变得更优美而简洁;例如,正旋函数 \( \sin\theta \) 的导数公式只是在 \( \theta \) 以弧度表示的情况下才成立:
图7中的特殊角度也可以用弧度来表示。在高中学三角函数时你可能是用图8里的值来记住这些特殊角度的 (我把这个表示法称作 \( \pi\)-弧度,以强调它是以 \( \pi\) 为单位的表示法)。


现在只需稍加思索你就会发现,如图9所示,这些所谓的“特殊”角无非只是一个整圆的有理数分数而已。如果我们回顾公式(4),把弧长 \( s \) 用圆周长 \( C\) 的分数 \( f \) 来重新表达, 也就是 \( s = f C \):
你会发现 \( \tau \) 就自然而然出现了。 如果你是 \( \pi \) 的忠实信徒,那么图10中显示的那些特殊角度的表达方式恐怕会完全动摇你信仰的根基。

尽管有很多证据可以证明 \( \tau \) 的好处,但是图10所展示的可能是最为直接而有力的证据了。从图10我们还能看出 Bob Palais 对于圆周率的本质意义的天才诠释:圆周率的内涵就是“绕圆一周”,\( \tau \) 是一个整圆的弧度大小。更令人欣慰的是,有了 \( \tau \) 以后你都不需要去强记特殊角了:十二分之一圆周就是 \( \tau/12 \), 八分之一圆周就是 \( \tau/8 \),如此类推。\( \tau \) 带给我们的不仅是一个清晰的概念而且还有弧度体系的各项优势;例如,\( \tau/12 \) 这个数所表达的抽象意义不但显而易见而且它本身也是一个无量纲的数:
最后我们来比较一下图8和图10,我们可以断定那些令人厌烦的 \( 2\pi \) 因子的来源:绕圆一周是 \( 1\tau \), 但是确要写成 \( 2\pi \)。虽然他们数理上是相同的,但是概念上却是迥异的。
2.2 圆周期函数
弧度体系已经为确立真正的圆周率提供了最强有力的论证,除此之外,我们还可以在其它场景下来比较 \( \pi \) 和 \( \tau \) 的优缺点。我们先来看两个基本的函数:\( \sin\theta \) (正弦函数)和 \( \cos\theta \)(余弦函数)。它们通常被称作“圆周期函数”因为它们给出的是单位圆(半径是 \( 1 \) 的圆)上的点坐标。正弦和余弦函数都是三角学里的重要函数(图11)

我们先通过圆周期函数的图形来研究一下它的特性6。从图12和图13里可以看到,它们都是周期为 \( T \) 的周期函数。图12里正弦函数的值 \( \sin\theta \) 从 0 开始,在第四分之一周期的时候达到最大值,在半周期的时候回到 0,在四分之三周期的时候达到最小值,最后在全周期的时候又回到 0。而余弦函数 \( \cos\theta \) 从最大值开始,在半周期的时候达到最小值,在四分之一和四分之三周期的时候回到 0 (图13)。两个图中 \( \theta \) 在这些特殊点上的值都是用弧度来表示的。


当然,正弦和余弦函数都是在单位圆上转了一整圈后经历了一个周期,在这里 \( T = \tau \);也就是说圆周期函数的周期和圆周率相等。这样一来,那些“特殊”的 \( \theta \) 值就变得一目了然了:四分之一周期是 \( \tau/4 \),半周期是 \( \tau/2 \) 等等。事实上,在我绘制图12的时候,我曾经一度在想当正弦函数值为零时 \( \theta \) 的值是多少。既然在半周期的时候正弦函数为零,而且 \( \tau \approx 6.28 \), 我于是能很快的用心算得到如下结果:
没错!我惊讶地发现我那时已经忘记了 \( \tau/2 \) 有时又叫做“ \( \pi \) ”这么一回事。如果刚才你也经历过这样的心路历程,那你我已经是心有灵犀了。
2.3 欧拉恒等式
这篇宣言如果不提到欧拉恒等式那就是我的失职了。欧拉恒等式被称为数学里最优美的公式。它里面的复指数和圆周期函数以及圆的几何结构有深层的联系。
下面的这个公式既可以当作一个定理来证明也可以直接作为一个定义来用。不管怎样看,它都是非常了不起的:
这个公式又叫欧拉公式(以莱昂哈德∙欧拉的名字命名)。这一公式把一个复指数函数和正弦函数,余弦函数,还有虚数单位 \( i \) 联系在一起了。尽管对这一公式的证明已经超出了本文的范畴,但是对它的证明在数学上是毋庸置疑的。而且其重要性也是为世人所公认的。
在公式(5)的 \( \theta = \tau \) 的地方取值我们就得到欧拉恒等式7:
用文字来描述,公式(6)给我们揭示的是这样一个基本原理:
以自然常数 e 为底的复指数函数在复平面旋转一周后等于 1
从几何学的角度来看,一个复数乘以 \( e^{i\theta} \) 相当于在复平面上将该复数旋转弧度 \( \theta \)。这也导出了对欧拉恒等式的另一个解释:
在复平面旋转一周的操作和乘以 1 的效果相同
既然任何数乘以 \( 1 \) 都和原数相等,那么 \( e^{i\tau} = 1 \) 的几何意义就是说在复平面上把一个点旋转一周,它将回到原来的位置上。
这使得我们可以看到,在弧度体系里,\( \tau \) 和在复平面上旋转一周的操作之间的联系是很自然的。 这一联系也使得欧拉恒等式听上去更像是一个重言式(Taugology)8。
不完美的公式
当然,我们知道欧拉恒等式的传统表示法里用的是 \( \pi \) 而不是 \( \tau \)。在欧拉公式 \( \theta = \pi \) 的地方取值进而导出以下等式:
但是负号在这里看着总是那么不顺眼,所以通常在表述公式(7)的时候大家总是将它重新排列成以下更为“优美”的形式:
推崇它的人进而还给这个重新排列后的欧拉恒等式赋予一些宏伟的意义。他们声称公式(8)将数学里最重要的五个数 \( 0 \), \( 1 \), \( e \), \( i \) 和 \( \pi \) 联系在了一起。
令人不可思议的是,就因为这一点,不知道有多少人抱怨说公式(6)只把这五个重要的数字中的四个数联系在了一起。那好吧,无需重新排列,我们只要把公式(6)写成以下的形式就可以满足他们的愿望了:
公式(9)无需重新排列就已经把数学中最重要的五个数 \( 0 \), \( 1 \), \( e \), \( i \) 和 \( \tau \) 联系在一起了。
欧拉恒等式表
众所周知,在任何公式的任何地方加一个零都不会改变原公式的本质,我们在公式(9)里引入一个 0 只是对 \( e^{i\pi} + 1 = 0 \) 的嘲弄罢了。但是对于 \( e^{i\pi} = -1 \) 有一点还是值得认真说明一下的。我们来看看如果把它用 \( \tau \) 来表示会是怎样:
从几何学的角度来看,它的意思是说把一个数在复平面旋转半周和乘以 -1 的效果是一样的。事实也是如此,在旋转弧度 \( \tau/2 \) 以后,复数 \( z = a + ib \) 被映射到 \( -a - ib \) 上,效果和 \( -1\cdot z \) 一样。
用 \( \tau \) 来重写公式(7)的欧拉恒等式能更直观地表达这一公式的几何意义,用 \( \pi \) 来写就没有这个效果(当然,\( e^{i\pi} = -1 \) 也可以用旋转弧度 \( \pi \) 来解释,但是人们几乎总是以 \( e^{i\pi} + 1 = 0 \) 的形式来描述欧拉恒等式,说明这个以 \( \pi \) 来表达的公式偏离了欧拉恒等式本质上所要传达的几何意义)。 公式(5)在 \( \tau/4 \) 处的取值 \( e^{i\tau/4} = i \) 也有类似的几何诠释:在复平面旋转四分之一周和乘以虚数单位 \( i \) 的效果相同;同样的,\( e^{i\cdot(3\tau/4)} = -i \) 表示在复平面旋转四分之三周和乘以 \( -i \) 的效果相同。以下表1总结了这些结果,我们称之为欧拉恒等式表:
| 旋转弧度 | 欧拉恒等式 | ||
| \( 0 \) | \( e^{i\cdot0} \) | \( = \) | \( 1 \) |
| \( \tau/4 \) | \( e^{i\tau/4} \) | \( = \) | \( i \) |
| \( \tau/2 \) | \( e^{i\tau/2} \) | \( = \) | \( -1 \) |
| \( 3\tau/4 \) | \( e^{i\cdot(3\tau/4)} \) | \( = \) | \( -i \) |
| \( \tau \) | \( e^{i\tau} \) | \( = \) | \( 1 \) |
我们将这样的分析再推进一步。对于任何一个弧度 \( \theta \),\( e^{i\theta} \) 所代表的是复平面单位圆上的一个点。复平面上的横轴代表复数的实部,竖轴代表复数的虚部,欧拉公式告诉我们 \( e^{i\theta} \) 对应的是复平面上的点坐标 \( (\cos\theta, \sin\theta) \)。 将图10中的“特殊”角度代入公式(5)中可以得到表2中的点坐标。将这些点画到复平面上就得到了图14的样子。把图14和图10 作一个比较你就不难判断二者中哪一个更能体现欧拉公式和圆的几何特性之间的关系。
| 极坐标形式 | 平面坐标形式 | 坐标点 |
| \( e^{i\theta} \) | \( \cos\theta + i\sin\theta \) | \( (\cos\theta, \sin\theta) \) |
| \( e^{i\cdot0} \) | \( 1 \) | \( (1, 0) \) |
| \( e^{i\tau/12} \) | \( \frac{\sqrt{3}}{2} + \frac{1}{2}i \) | \( (\frac{\sqrt{3}}{2}, \frac{1}{2}) \) |
| \( e^{i\tau/8} \) | \( \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i \) | \( (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) \) |
| \( e^{i\tau/6} \) | \( \frac{1}{2} +\frac{\sqrt{3}}{2} i \) | \( (\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( e^{i\tau/4} \) | \( i \) | \( (0, 1) \) |
| \( e^{i\tau/3} \) | \( -\frac{1}{2} +\frac{\sqrt{3}}{2} i \) | \( (-\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( e^{i\tau/2} \) | \( -1 \) | \( (-1, 0) \) |
| \( e^{i\cdot(3\tau/4)} \) | \( -i \) | \( (0, -1) \) |
| \( e^{i\tau} \) | \( 1 \) | \( (1, 0) \) |

3 圆面积:致命的一击
如果你是一个 \( \pi \) 的忠实信徒,读到这里的时候你也许已经开始怀疑你的信仰了。\( \tau \) 实在是太自然太直接了当了,难道就没有一个 \( \pi \) 更胜一筹的例子吗?记忆里好像有这么一个例子可以让 \( \pi \) 扳回一局,那就是圆的面积公式:
看到这里你会说:“不对,等一下。圆的面积公式不是一直都是像以下的公式一样用半径来表示的吗?”
这个公式最先是由阿基米德证明出来的。它也是数学中最重要的公式之一。它用的就是 \( \pi \)! 终于可以为 \( \pi \) 挽回一点面子了。 可是,这一节的题头却给出了一个不详预兆。 如果这个公式代表了 \( \pi \) 的终极荣耀,那为什么我们却说这是对它致命的一击呢?
3.1 二次型
让我们来看看这个 \( \pi \) 的模范公式 \( A = \pi r^2 \)。我们注意到这里面涉及了直径,等一下,不对,是半径,的二次方。所以这个公式是一个简单的二次型。二次型在很多地方都会出现。作为一个物理学家,我最喜欢的二次型的例子来自基础物理学的课程。下面我们来看几个这样的例子:
均匀重力场里的自由落体运动
伽利略发现在均匀重力场中自由落体的速度和它落下的时间成正比:
这个正比例系数就是重力加速度 \( g \):
落体的速度是下落距离对时间的导数,因此我们可以用积分计算在某一时间自由落体落下的距离:
线性弹簧的势能
Robert Hooke 发现拉伸一个弹簧所需要的力和拉伸距离之间成正比:
这一关系的正比例系数是弹簧的弹力系数 \( k \)9:
于是弹簧被拉伸以后的势能等于外力做的功,也就是:
运动物体的动能
牛顿发现施加在一个物体上的力和它的加速度成正比:
这个正比例系数就是物体的质量 \( m \):
于是这个运动物体的能量,也就是动能,等于外力通过将质量为 \( m \) 的物体加速到速度 \( v \) 所做的功,也就是:
3.2 一个不详的预感
看了以上在物理学中出现的二次型的例子以后,我们再回到圆的几何学上来,这时你可能已经有了一些不详的预感。这是可以理解的。

如图15所示,在计算圆的面积时,我们可以把圆想象成由一系列周长为 \( C \) 宽度为 \( dr \) 的圆环组成的。每一个圆环的面积是 \( C\,dr \):
我们知道,圆的周长和它的半径成正比:
这个正比例系数就是 \( \tau \):
圆的面积就是这些圆环面积的积分:
如果在这一节开始的时候你还是 \( \pi \) 的同党,读到这里的时候恐怕你也已经要倒戈了。因为即使是在这个 \( \pi \) 应该更胜一筹例子里(\( A= \pi r^2 \)),\( \pi \) 显然掩盖了圆面积公式的二次型表达式的基本结构:因为二次型的基本因子 \( \textstyle{\frac{1}{2}} \) 和 \( \pi \)前面本应该有的因子 2 抵消了。 事实也是这样,阿基米德最初给出的证明并没有导出圆的面积公式是 \( \pi r^2 \) 的结论,而是说圆的面积等于一个底为 \( C \) 高为 \( r \) 的直角三角形的面积。引用三角形的面积公式我们得到:
所以说想躲避 \( \textstyle{\frac{1}{2}} \) 这个二次型因子是不可能的(表3)。
| 数学/物理量 | 符号 | 表达式 |
| 自由落体下落距离 | \( y \) | \( \textstyle{\frac{1}{2}}gt^2 \) |
| 弹簧势能 | \( U \) | \( \textstyle{\frac{1}{2}}kx^2 \) |
| 物体动能 | \( K \) | \( \textstyle{\frac{1}{2}}mv^2 \) |
| 圆面积 | \( A \) | \( \textstyle{\frac{1}{2}}\tau\,r^2 \) |
Q.E.D. 证明完毕
我们从宣言的开始通篇都是为了说明为什么 \( \tau \) 才是真正的圆周率。既然圆的面积公式是 \( \pi \) 的最后一根救命稻草,行文至此我可以斗胆宣布: Q.E.D.(证明完毕)。
4 冲突和抵抗
尽管 \( \tau \) 的优越性显而易见,很多人还是反对接受这个数字和符号。在这一节里,我们先排除一些人对采用 \( \tau \) 这个字母的忧虑,然后我们再反驳一些人对采用 \( C/r \) 所持的反对意见(这其中包括一篇为维护 \( \pi \) 的统治地位所写的《Pi 宣言》的文章)。在这一节里,我们要讨论一些涉及到超球体(第5.1节)的体积一类的较高深的数学课题,对这些课题的讨论可以进一步补充和强化我们在第3节所提出的关于圆面积的一些论证。
4.1 绕圆一周
对一个符号合理性的终极检验是看它的应用。我们在这篇宣言里通篇都看到了 \( \tau \) 的用处,至此你可能已经接受了它所扮演的重要角色。但是对于像 \( \tau \) 这么基本的数学常数来说,如果能从更深一层的意义上来说明选择这个符号的原因那就再好不过了。比如说,为什么不用 \( \alpha \) 或 \( \omega \) 呢?选 \( \tau \) 这个符号有什么特别的理由吗?
选择用 \( \tau \) 来表示圆周率有两个主要原因。第一 \( \tau \) 和 \( \pi \)看上去很像,形同手足。几个世纪以来,\( \pi \) 和圆周率所形成的的联系是根深蒂固而无法回避的。与其和它抗争,还不如用 \( \tau \) 来顺水推舟(事实上,这两个符号里都有一个短横线。我们可以把短横线以下竖立的像脚一样的部分看作是分母。 \( \pi \) 在分母里有两只脚,而 \( \tau \) 只有一只脚,这样来看, \( \tau = 2\pi \) 就再自然不过了10)。
第二个原因是,\( \tau \) 代表的是一个圆周,也就是“一转(Turn)”的意思。你可能已经注意到了“\( \tau \)”和英文的“Turn”的发音都是以“t” 开头的。这也是为什么选择 \( \tau \) 的最初原因,而非巧合。因为英语单词“Turn”在希腊语里对应的词是 τόρνος (tornos), 意思是车床。τόρνος 的第一个字母用数学字体写出来就是:\( \tau \)。
自从《Tau 宣言》发表以来, 我还了解到 Peter Harremoës 在 2010 年的时候向《\( \pi \) 是错误的!》的文章作者 Bob Palais 提议用 \( \tau \) 取代 \( \pi \)。John Fisher 曾在 2004 年一篇 Usenet 发帖里提出了 \( \tau \) 的概念。Joseph Lindenberg 早在 20 年前就预料到了对 \( \tau \) 的论证及其符号的使用11!Harremoës 博士还特别强调了我在第 1.1 节中首次阐述的一个观点的重要性:\( \tau \) 给了圆周率一个名字。\( \tau \) 也是一个常用的希腊字母,第一次看见这个字母的人都可以立刻说出它的发音。我们也许可以把圆周率就叫做 “turn” (一转),但相比之下, \( \tau \) 在书写和发音的时候更加方便。比如,我们可以说四分之一圆周的弧度是“one quarter turn”,这听上去还不错,但是如果说四分之一圆周的弧度是 “turn over four”(英文口语里用来表达分数的惯用法)就有点怪异了。而且如果说圆的面积是 “one-half turn \( r \) squared” 听上去就更奇怪了。但是如果用 \( \tau \) 来代替,我们说一个角的弧度是 “tau over four” 或者说圆的面积大小为 “one-half tau \( r \) squared” 就很自然。
(译者注:因为中英文对分数和公式的口头描述方式的不同,中文读者对以上的说法可能没有英文读者感受那么强烈)符号歧义
当然,引进任何一个新的符号都有可能和现在的用法产生冲突。 正如我们在第 1.1 节里提到的,《\( \pi \) 是错误的!》那篇文章提议用一个新的符号来表示圆周率(见图3)。这种做法也是有先例的。比如在量子力学发展的早期,Max Planck 引入了一个常数 \( h \)。这个常数把光子的能量和它的频率通过公式 \( E = h\nu \) 联系起来。但是物理学家很快意识到,用 \( \hbar \)(读作 “h-bar”)更为方便。\( \hbar \) 就是 \( h \) 除以 \( 2\pi \),如今这个用法已经成了标准。
但是要人们接受一个新的符号还是不容易的。它首先要有一个名字,这个名字还必须推广开来,然后这个符号本身还要加入到文字处理和排版系统中去。而且,为 \( 2\pi \) 颁布一个新的符号需要学术界的通力合作。目前就学术界对 \( \pi \) 和 \( \tau \) 之间的争论来看,这一合作的意向不但少得可怜,甚至充满敌意。所以,用现有的符号给圆周率命名可以让我们在的当今的数学体制下迂回推进。12
与其推广一个新的符号,《Tau 宣言》建议采用现有的希腊字母。因此,既然 \( \tau \) 已经在现在的一些学术场景下被采用了,我们就必须解决新的用法和现有用法之间可能存在的冲突。值得庆幸的是,这样的冲突并不多见。尽管 \( \tau \) 已经在某些领域用来表示某些“特定”的变量,比如,机械工程里的剪应力,旋转机构的扭矩,以及狭义和广义相对论里的原时等等, 除此之外 \( \tau \) 并没有和现有的符号用法发生普遍的冲突13。对于以上出现冲突的情况,我们或者可以容忍一定的歧义,或者适当修改现有的符号来绕过它。比如用 \( N \) 来表示扭矩14 或者用 \( \tau_p \) 来表示原时等等。
尽管有以上的解决方案,但是对一些人来说,潜在的符号用法冲突却一直是他们反对接纳 \( \tau \) 的主要原因。一些人甚至完全否认 \( \tau \) (或者任何其它现在使用符号)能够克服这些问题。但事实上科学家和工程师对符号的歧义有很高的容忍度,声称圆周率 \( \tau \) 不能和其他用法共存就是否认这一普遍存在的事实。
我们可以从量子力学里找到一个例子来说明学术界是可以容纳一定程度上的符号歧义的。 例如波尔半径(笼统的说)指的是氢原子在其最低能量状态(基态)时的“尺寸”,它的计算公式如下:
这里 \( m \) 代表电子的质量,\( e \) 代表其电荷。同时,基态本身是由波函数的值来描述的。在半径 r上的波函数值随着 r 和波尔半径的比例以指数形式降低。
这里面 \( N \) 是一个规范后的常量。
你注意到什么问题了吗?可能没有。这也正是我想说的。这里的“问题”是,波尔半径公式里的 \( e \) 和波函数里的 \( e \) 不是同一个 \( e \)。前一个 e 表示的是电子的电荷,后一个 e 是自然常数(自然对数的底)。如果我们将 \( a_0 \) 在公式(10)的指数变量里展开,我们就得到如下的公式:
也就是说 \( e \) 的指数里含有另外一个 \( e \)。这个情况实际上比看上去更糟糕,因为 \( N \) 里面也有一个 \( e \),如果继续展开的话,我们就得到:
我可以毫不怀疑地说,如果自然常数现在还没有自己的符号,任何人如果提议用 \( e \) 来表示自然常数,大家都会说这绝对不行,因为这和 \( e \) 的其它已有的用法冲突。然而实际上没人认为 \( e \) 在以上两种情况下的重复使用会带来任何问题。还有很多其它类似的例子,有的情况下甚至连 \( \pi \) 本身都被用来表示两种不同的东西15。所以很难理解为什么用 \( \tau \) 来表示不同的数就会有问题。
顺便说一句,可能不少 \( \pi \) 的崇拜者马上注意到氢原子基态波函数有一个 \( \pi \) 的因子:
乍一看上去这似乎比用 \( \tau \) 来得自然:
就像我们常说的,表象总是有一定的欺骗性:\( N \) 其实是以下几项因子的乘积
它显示了圆周率是通过 \( 1/\sqrt{2\pi} \) 也就是 \( 1/\sqrt{\tau} \) 项引入公式的。和圆的面积公式的情形一样,因子 2 抵消以后留下了 \( \pi \) 只是一个巧合。
4.2 Pi 宣言
据我所知的大多数对 \( \tau \) 的反对声音来自零星的电邮和网上论坛的回帖,除此之外,反方还发起了一个有组织的抵抗运动。 这其中值得一提的是,在《Tau 宣言》于 2010 年 6 月发表以后,网上也出现了一篇叫《Pi 宣言》的文章来为 \( \pi \) 提供辩护。 这一节以及之后的两节的内容就是为了反驳那篇文章中的观点。出于必要的考虑,这几节的内容可能会比文章其它的部分更高深一些,但是只要抱着一定的好奇心读下去,你就会大致理解为什么《Pi 宣言》里陈述的论点是站不住脚的。
《Pi 宣言》的出现反映了人们对这一议题的持续关注,这虽然是一个好的现象,但是宣言里的一些主张却是错误的。举个例子,《Pi 宣言》里提到高斯正态分布公式里出现的 \( 2\pi \) 因子只是一个偶然,它可以用以下“更为自然”的形式来表达:
这种说法是不对的。\( 2\pi \) 的出现是因为把非规范化的高斯分布平方以后再换成极坐标而生成的,在极径上积分得到因子 1,在极角上积分得到因子 \( 2\pi \)。就像在圆面积公式里那样,\( \pi \) 因子的出现是因为 \( 1/2\times 2\pi \),而不是从 \( \pi \) 本身独立导出的。
《Pi 宣言》里还有另外一个相关的论点,说伽马函数在 \( 1/2 \) 处的取值用 \( \pi \) 来表达更为自然:
这其中
但是 \( \Gamma(\frac{1}{2}) \) 和正态分布一样都包含了高斯积分(当 \( u = x^{1/2} \) 时),因此 \( \pi \) 在这里其实就是 \( 1/2\times 2\pi \)。在许多《Pi 宣言》里引用的例子里,圆周率都是因为全极角积分运算(也就极角 \( \theta \) 从 \( 0 \) 到 \( \tau \) 的积分)而引入的。
《Pi 宣言》里还提到了一些关于规范多边形(英文叫 \( n \)-sided polygons 或 “\( n \)-gons”)的公式。比如说它提到 \( n \) 边形的内角和可以用以下公式计算:
这个问题在《Pi 是错误的!》一文中已经讨论过:“三角形的内角和是 \( \pi \) 没有错。但是任意多边形的外角和(用它可以很容易地导出多边形的内角和)却是 \( 2\pi \)。这一结论也可以更进一步推广到任意简单闭环的曲率积分上,其结果也是 \( 2\pi \)”。除此之外《Pi 宣言》还提到了计算具有单位半径(从中心到角点的距离)的 \( n \) 边形面积的公式:
声称这是 \( \pi \) 的一个“显而易见的胜利”。但是如果我们将此公式用倍角定理 \( \sin\theta\cos\theta = \frac{1}{2} \sin 2\theta \) 变换一下,可以得到
也就是
这说明了 \( n \) 边形的面积公式里有一个自然因子 \( 1/2 \)。如果把公式(12)里的 n 取极限 \( n\rightarrow \infty \)(并应用 L’Hôpital’s rule)就得到一个有无数个边的半径为 1 的正多边形的面积:也就是单位圆的面积
在这里,我们注意到《Pi 宣言》因此大张旗鼓的宣称 \( \pi \) 代表了单位圆的面积,四分之一单位圆的面积就是 \( \pi/4 \) 等等。 于是断定 \( \pi \) 在这种情形里略胜一筹,就像 \( \tau \) 在弧度体系里有它的优势一样。 可是遗憾的是,就像在第 3 节和公式(13)里我们所看到的,在计算圆的面积时,因子 \( 1/2 \) 是自然产生的。用单位圆面积为 \( \pi \) 辩护只是牵强附会。事实上,我们知道角度为 \( \theta \) 的扇形面积公式是:
圆的面积就是以上公式 \( A = \frac{1}{2} \tau\, r^2 \) 在 \( \theta = \tau \) 的地方取值。因此无论如何也没有办法回避因子 1/2 的出现。
所以对角度的测度和对面积的测度是不同的。在角度公式里没有自然因子 \( 1/2 \),但是在面积公式里,因为要对一个和简单二次型相关的线性函数进行积分,所以因子 \( 1/2 \) 便自然而然地出现了。下一节我们将要进一步探讨为什么 \( \pi \) 的处境比看上去还要糟糕。
5 探求 Pi 和 Tau 的本质
我一直以来都为这一课题的丰富内涵留而着迷,因此我对 \( \pi \) 和 \( \tau \) 的理解也不断深入。在 2012 年的 Half Tau Day(3月14日)那天,我认为我找到了 \( \pi \) 的根本缺陷。我当时的论点是建立在对 \( n \) 维球面和球体的分析上的,由这一分析所得出的结论是:\( \pi \) 这个数不具有任何基本几何内涵。有一个叫 Jeff Cornell 的《Tau 宣言》的读者也向我指出了我当时的分析还不够完备。所以,这一节我们不但要完全否定 \( \pi \) 的意义,而且要对 \( \tau \) 的真实含义作一个明确的阐述。因为它的真实含义比我原来想象的要更加深刻和微妙。
提示: 这一节的内容比文中其它部分要更深奥一些。如果你跳过这一节不读也不会影响文章的连贯性。如果你对这一节的内容理解有困难,我建议你直接跳到第 6 节。
5.1 超球体的面积和体积
我们先来探讨如何把圆的定义扩展到任意多维空间16。这样的概念叫做超球体或 \( n \)-维球。它的定义如下17所述(为了方便,我们假设这些球都是以坐标原点为中心的)。一个 \( 0 \)-维球是一个空集,我们把它的“内部”空间定义为一个点18。一个 \( 1 \)-维球面则由所有满足以下条件的所有点构成:
也就是两个点 \( \pm r \)。它的内部空间是满足以下公式的所有点
这也就是从 \( -r \) 到 \( r \) 之间的一个线段。 一个 \( 2 \)-维球面是一个圆,它由满足以下条件的所有点构成
它的内部空间是由满足以下条件的所有点构成
这就是一个圆盘。同样道理,一个 \( 3 \)-维球面上的点满足以下条件
其内部空间就是一个球体。我们可以把这一概念以此类推到 \( n \) 维空间,尽管我们很难想象 3 维以上空间里的几何形状, 但是数学上并不复杂。一个 \( n \)-维球的球面就是由满足以下条件的点所组成
《Pi 宣言》里(参见第 4.2 节)引用了单位 \( n \)-维球的体积公式来为 \( \pi \) 作辩护:
这里的伽马函数由公式(11)给出。公式(14)只是 \( n \)-维球的体积公式在半径 r=1 时的一个特例。对于任意半径 r,如果用 \( \pi \) 来表示,这个公式的广义形式是这样的:
因为 \( V_n(r) = \int S_n(r)\,dr \),我们也知道 \( S_n(r) = dV_n(r)/dr \),因此 \( n \)-维球的面积公式可以写成:
让我们来分析一下这个公式的内部结构,它能在我们比较 \( \pi \) 和 \( \tau \) 时提供一些有力的论证。我们先从这个公式看似简单的表象来分析。虽然伽马函数看似简单,它实际上是一个在半无限域上的积分,这就已经不简单了。好在伽马函数在某些特例下可以简化。比如当 \( n \) 是整数时,我们可以用分段积分法得到如下的形式
从这个角度来看,\( \Gamma \) 函数可以理解为阶乘函数在实数域上的推广19。
在 \( n \) 维超球的面积和体积公式里, \( \Gamma \) 函数的参数不一定是整数,而是 \( \left(1 + \frac{n}{2}\right) \),它在 \( n \) 为偶数时是整数,而在 \( n \) 为奇数时它是就不是整数了。考虑到这一点,伽马函数应该按以下的形式表达。这个表达式是从 Wolfram MathWorld 里引用过来的,而且按惯例,公式里用的是 \( \pi \) :
对 \( r \) 积分后得到:
让我们来看一下公式(18)的细节。我们注意到 MathWorld 用到了双阶乘函数 \( n!! \),但是很奇怪的是它只用在当 n 为奇数时的表达式里(我先在此埋一个伏笔)。虽然双阶乘函数在数学里不常见,但它却是基本函数之一。它和普通的阶乘函数基本一样,只不过双阶乘函数是每隔两个数递减相乘。比如,\( 5!! = 5 \cdot 3 \cdot 1 \) 和 \( 6!! = 6 \cdot 4 \cdot 2 \)。写成一般形式时是这样的:
(根据定义 \( 0!! = 1!! = 1 \)) 我们也注意到公式(19)被自然分解成了偶数和奇数的情形,对于为什么 MathWorld 只在奇数的情形下使用双阶乘函数还是很令人费解的。
为了解开这个迷,我们来细看一下公式(18)在 \( n \) 为奇数时的情形:
对于以下的公式部分
我们也可以将其写成这个形式
这里我们又看到老朋友 \( 2\pi \) 了。
现在我们来看公式(18)在 n 为偶数时的情形。我们在前面已经注意到它在偶数的情形下用一般的阶乘函数而在奇数的情形下用双阶乘函数,这的确很奇怪。双阶乘函数的定义已经是分段式的了,如果公式(18)里的偶数和奇数情形都可以用 \( n!! \) 来表示,那么我们就可以把它当公因子提出来写成以下的形式:
可是,阶乘和双阶乘函数之间有什么联系吗? 有!当 \( n \) 时偶数时这两个函数之间有如下的联系:
(用数学归纳法可以很容易证明以上的等式) 把以上公式代入超球的体积公式中当 \( n \) 为偶数时的情形就得到:
它和以下的公式非常相似
这里我们又遇上了 \( 2\pi \).
把以上的结果都带入公式(18),我们可以得到:
而公式(17)可以重写为
让 \( \tau=2\pi \),于是公式(21)可以写成:
为了更近一步简化这个公式,我们可以引入向下取整函数 \( \lfloor x \rfloor \)。这个函数就是一个取小于或等于 \( x \) 的最大整数的操作(相当于把分数部分去掉,例如 \( \lfloor 3.7 \rfloor = \lfloor 3.2 \rfloor = 3 \))。于是我们得到
这样一来,以上公式就可以简化成:
对公式(22)在 \( r \) 上积分可以得到
Lambda (\( \lambda \))
公式(22)和公式(23)的表示形式已经比前面用 \( \pi \) 的公式(17)和公式(18)有很大改进了。但是我们在此基础上还可以用直角的弧度对公式进一步简化20:
我们在后面的第 5.2 节将会看到,公式(24)可以用更为自然的体现圆的对称性的形式来表示:
这里的因子 \( 2^2 \) 来自 2 维空间的 \( 2^2 \) 个全等圆弧(每个象限一个,一共四个)。
用 \( \lambda \) 的最大好处是它可以统一公式(22)和公式(23)里的奇数和偶数表达式,因为这两个表达式里都有因子 \( \tau^{\left\lfloor \frac{n}{2} \right\rfloor} \)。将公式(25)代入这个因子于是得到
也就是说,我们可以把以下的乘积
写成这样
于是我们的表达式可以不必区分奇偶性了。将公式(26)代入公式(22)和公式(23)可以得到
以及
简化后的公式(27)和公式(28)看上去似乎多引入了一个因子 \( 2^n \),但是它却有很明确的几何意义:\( n \) 维球在 n 维空间里可以自然分成 \( 2^n \) 个全等的部分,它们对应于方程 \( \sum_{i=1}^{n} x_i^2 = r^2 \) 的 \( 2^n \) 个解(也就是 \( \pm x_i \) 的排列组合)。在 2 维空间,它们对应的是被四个象限分割成的 4 个等长的圆弧段;在 3 维空间里,它们对应的则是被八分象限分割成的 8 个全等的部分球体;以此可以类推至任意维度空间的超球体的情形。也就是说,我们可以利用超球体的对称性,先计算它在多维空间第一象限部分(对于所有 \( i \),\( x_i > 0 \))的面积或体积,然后把它乘以 \( 2^n \) 就可以得到整个超球体的面积或体积了。
据我所知公式(27)和公式(28)已经是最简单的超球体表面积和体积的公式了(而且这也是我唯一能一直记住的公式形式)。就拿体积公式来说,不像公式(15)表面貌似简洁的假象,公式(28)里没有积分符号,只有略微少见但仍然属于基本函数类型的向下取整函数和双阶乘函数。一个半径为 1 的 \( n \) 维单位超球的体积就是用它在单一象限里的体积 \( \lambda^{\left\lfloor \frac{n}{2} \right\rfloor}/n!! \) 乘以 n 维空间的象限数 \( 2^n \)。
递推关系
从公式(27)和公式(28)我们可以看出它们是用直角 \( \lambda \) 表示的最简洁的形式了。但是,我们对 \( \tau \) 的探讨还没有结束。
在公式(28)中,超球的体积公式被自然地分成了两个部分,它们分别对应于奇数维空间和偶数维空间两种情形。也就是说 4 维空间里的超球体积公式 \( V_4 \) 只和 \( V_2 \) 有关,和 \( V_3 \) 无关。而 3 维空间里的超球体积公式 \( V_3 \) 只和 \( V_1 \) 有关,和 \( V_2 \) 无关。但是,它们之间的联系到底是怎样的呢?
我们可以在不同维度空间的公式递推关系里寻找答案21。在这里,我们把 \( n \) 维超球的体积除以 \( (n-2) \) 维超球体积:
我们从公式(29)里可以看到,我们可以把 \( (n-2) \) 维超球的体积乘以 \( r^2 \)(这是维度分析里必要的因子),然后除以 \( n \),再乘以“递推常数” \( 2^2\lambda \) 就能得到 n 维超球的体积。
同样,对于超球的面积公式:
递推常数 \( 2^2\lambda \) 扮演了同样的角色。
因此在公式(29)和公式(30)里确立不同维度空间的公式递推关系的常数不是 \( \lambda \) 而是 \( 2^2\lambda \)。 和公式(25)比较一下我们发现这个常数就是 \( \tau \)! 而且,如果我们用另一种更直接的递推公式来算体积(在 \( r \) 的地方用 \( R \) 来表示),可以算出积分:
这也显示了 \( \tau \) 作为递推常数出现在公式里并非出于偶然。递推常数和圆周率确实是同一个数
因此,是 \( \tau \)(而不是 \( \lambda \))建立了偶数解和奇数解之间的关系。Joseph Lindenberg 在他的文章《Tau Before It Was Cool》里对此有很清楚的描述(Figure 16)22。
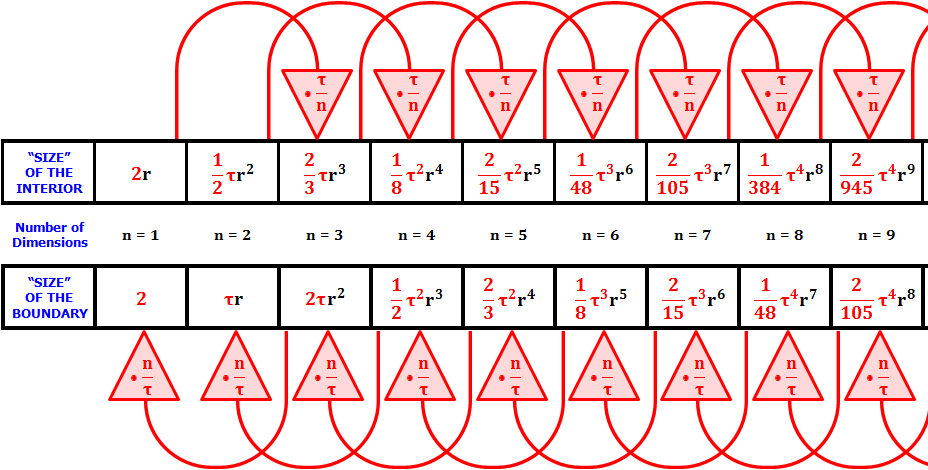
当我们讨论一般的 \( n \) 维球时,为方便起见我们会像在公式(27)和公式(28) 那样用 \( \lambda \) 来表示面积和体积。但在 \( n \) 为任意一个指定值时的公式, 我们则用递推常数 \( \tau \) 来表达。
5.2 三个常数族
用我们在第 5.1 节所做的铺垫,我们现在可以来锁定 \( \pi \) 和 \( \tau \) 的本质不同了。为了把这个课题深挖到底,我们用公式(27)和公式(28)来定义两个常数族,然后用定义 \( \pi \) 的方式(公式1)来定义第三个常数族,以此来说明 \( \pi \) 的问题在哪里。
首先,我们先来定义一个“表面积常数族” \( \tau_n \)。这个无量纲的常数族可以通过把公式(27)除以 \( r^{n-1} \) 而得出:
然后,我们来定义一个“体积常数族” \( \sigma_n \)。这个常数族可以通过把体积公式(公式28)除以 \( r^n \) 而得到:
根据公式(32)和公式(33)定义的常数族,我们于是可以把面积和体积公式(公式27和公式28)写成以下的简化形式:
以及
通过体积和面积的积分关系 \( V_n(r) = \int S_n(r)\,dr \),我们可以得出以下的结论:
我们来观察一下这两族常数。\( \tau_n \) 这个常数族有很重要的几何意义:当公式(32)里 \( r=1 \) 时,我们可以看到 \( \tau_n \) 就是单位 \( n \) 维超球的表面积,同时也是 \( n \) 维球的全方位角度。如果把 \( s_n(r) \) 看成是 \( n \) 维空间的“弧面片”(整个球面积 \( S_n(r) \) 的 \( f \) 分之一 ), 我们就得到
这里的 \( \theta_n \) 只是 2 维空间的弧度概念在 n 维空间的推广。我们可以看到 \( \tau_n \) 则是“圆周”的概念在 \( n \) 维空间的推广。这也解释了为什么 2 维球(也就是圆)的常数 \( \tau_2 = 2^2\lambda = \tau \) (圆周率)可以很自然地对应到图10中去。而且,我们从第 5.1 节里知道,\( \tau_2 \) 也是 \( n \) 维球面和球体公式的“递推常数”。
而与此同时 \( \sigma_n \) 则代表了 \( n \) 维单位超球的体积。其中,\( \sigma_2 \) 是单位圆的面积:
从这里我们可以看到 \( \sigma_2 = \tau/2 = 3.14159\ldots \) 这个数的确有它的几何意义。可是,它和周长或直径却无任何关系。也就是说 \( \pi = C/D \) 不是 \( \sigma_n \) 常数族的一员。
那么 \( \pi \) 到底是属于哪一个常数族呢?如果我们把公式(1)用多维空间推广的形式写出来:
我们因此看到 \( \pi \) 很自然的属于一族由超球面积除以直径的指数而导出的无量纲常数。这就是我们说的第三个常数族 \( \pi_n \):
我们在公式(34)中做一个 \( D = 2r \) 的替换,然后代入公式(32) 就得到用 \( \tau_n \) 来表达的公式:
我们现在终于可以知道 \( \pi \) 的问题在哪里了。 \( 3.14159\ldots \) 这个数唯一的几何意义就是它是单位圆元的面积。但是这一数字来自 \( \sigma_n = \tau_n/n \) 在 \( n=2 \) 时的取值:
这个值等于 \( \pi_2 \) 是没错:
但是这只是一个偶然。因为 \( 2^{n-1} \) 只在 \( n=2 \) 时才等于 \( n \)(也就是,\( 2^{2-1} = 2 \))。在其它任何高维度的情形下,\( 2^{n-1} \) 都不等于 \( n \)。也就是说,\( \pi \) 所谓的几何意义只不过是一个数学上的巧合罢了。
6 总结
这些年来我听过很多反方的观点说 \( \pi \) 并没有任何问题,亦或是 \( \tau \) 也没有任何优点,所以在做最后总结之前,我想先回答一些大家对这个课题提出的常见问题。
6.1 常见的问题
- 你是认真的吗? 我当然是认真的。因为我觉得这个课题本身很有趣,所以我在谈论它时的语调可能经常略显轻松,但是我的目的是很严肃的。把圆周率定义成周长和直径的比是一个笨拙且令人混肴的惯例。尽管我希望看到数学家们改变这一现状,但我对他们并没有什么可担心的。我最担心的是那些刚开始学习数学的新手,因为这对他们伤害最深。 就像第 2.1 节里说的,\( \pi \) 是一个教学法的灾难。你可以试试去和一个12岁(或30岁)的人解释为什么八分之一圆周(把它想象成一块比萨饼)的角度是 \( \pi/8 \),哦不对,应该是 \( \pi/4 \)。你看到问题在哪里了吗?这种人为的混淆简直让人抓狂,可以说是近乎变态。
- 我们怎么才能用 \( \tau \) 最终取代 \( \pi \) 呢? 你下一次写公式时如果要用到圆周率,记得先注明:“为了方便起见,我们在这里用\( \tau = 2\pi \)”,然后继续(当然有人会问:“为什么要这样做呢?”。你可以给他们指一个方向让他们自己去找答案。或者你可以告诉他们,有人已经就此写了一篇宣言来解释,自己去看看吧)。 总之,如果想让大家都开始用 \( \tau \) 就得先从自己做起。
- 现在改是不是太晚了?所有的教科书和数学论文难道都要重写吗?
不晚,也不需要重写教科书。的确,有些现有的习惯用法是没法改变的。比如说,本杰明∙富兰克林选择了用正号来表示电荷,进而导致我们熟悉的电流(金属里的自由电子)一直都是给人以正电荷在流动的印象,而实际上电荷的载体却是带负电的。这个令人困惑的负号对物理系的新生来说是一个永远的魔咒23。要想改变这个惯例就得重写所有课本(还要烧掉旧课本),如若不然,读者不可能一眼就能分辨出书里用的是哪个规范。
相比而言,尽管 \( \pi \) 是没办法重新定义了,但是我们却可以用以下的公式变换把 \(
\pi \) 立即换成 \(
\tau \) 而不会引起任何混乱
\[ \pi \leftrightarrow \textstyle{\frac{1}{2}}\tau. \]
这只是一个机械的替代操作而已。这个操作既稳健又完全可逆。所以从 \( \pi \) 到 \( \tau \) 的转变可以一步步地进行,不必一步到位。
- 用 \( \tau \) 会给大家(尤其是学生们)带来混乱吗? 如果你能理解弧度的概念,那你对 \( \tau \) 的掌握则是轻而易举的事。你也能很容易理解为什么 \( \tau \) 比 \( \pi \) 的概念更清晰。况且,说“让 \( \tau = 2\pi \)”并没有什么会让人觉得难懂的。狭义地来理解,这就只是一个符号替换而已。而且我们还可以把这个话题当成一个教学的机会。\( \pi \) 可能是错的这个想法本身就很引人入胜,学生们可以和教材互动,把里面所有用到 \( \pi \) 的公式换成用 \( \tau \) 来表示,让他们自己判断哪一个用法更好。
- 这样的工作有意义吗? 这个工作当然有意义。圆周率是一个很重要的数学概念。人们对它是非常重视的。人们为它著书立作,而且还在一年中的某一天庆祝它,甚至有人还能背诵到它成千上万位的数字。我对此也很重视,所以我才写了这篇宣言,你对此也一样重视,所以你才把这篇宣言一直读到这里。正因为它很重要,所以一时很难让大家承认现在的习惯用法是错误的 (你怎么向 Pi 的数字记忆世界纪录保持者 Rajveer Meena 解释说他所能背诵的 70,000 位数字其实只是来自一个真正的圆周率的一半的数呢?)。既然圆周率很重要,那么为它正名就同样重要。我们在这篇宣言里已经看到了,\( \tau \) 才是真正的圆周率。虽然 \( \pi \) 在历史上有其一定的地位,但是它在数学上的意义则仅仅只是因为它的值是 \( \tau \) 的二分之一而已。
- 那为什么人们一开始就用 \( \pi \) 呢? 作为一个数学符号,\( \pi \) 最初是在 300 年前由欧拉推广采用进而流行起来的(史料引用自 William Jones 的著作),但是 \( \pi \) 这个数字的具体起源则已经消失在时间的迷雾中了。我猜想人们用 \( C/D \) 而不是 \( C/r \) 来计算圆周率可能是因为测量一个圆的直径比测量半径更容易。但是,这并不能成为这个数学瑕疵的借口。我很奇怪为什么连阿基米德(它因为用逼近法算出圆周率的近似值而著名)都没有意识到 \( C/r \) 是一个更基本的常数。而更让我觉得奇怪的是,欧拉也没有抓住改正这个错误的机会。和阿基米德不一样的是,欧拉所处的时代已经有了现代代数法的工具(就像我们从第 2.1 节开始所看到的),而这些数学工具原本可以把圆和圆周率之间的底层关系说明得一清二楚。令人不可思议的是,欧拉还曾经在不同场合下用同一个符号 \( \pi \) 来表示 \( C/D \) 和 \( C/r \)!可十分令人遗憾的是他竟然没有把更方便的那个选择定为标准加以推广。
- 为什么你会对这个课题感兴趣? 首先我作为一个寻求真理的人对任何解释的合理性都是很看重的。第二,作为一个教师我也看重解答问题时思路的清晰和简洁性。第三,我也是一个骇客,我喜欢这样的挑战。第四,作为一个学过历史和人类学的学生,我认为 \( \pi \) 的定义是很荒诞的,但是它竟然能在人们的眼皮底下存在这么多个世纪而无人质疑。况且,那些支持真正圆周率的人大都是最理性最聪明的人。还有什么比这些更能说明这个课题引人入胜的原因呢?
- 你的脑筋没问题吧? 我脑筋当然没有问题,大家不用为我操这份心。我除了偶尔会穿一些怪异的鞋子以外,其它地方看上去都和常人一样。但是你可能怎么也猜不到的是,我有一点和大多数人不一样:我是一个名声在外的数学狂人。
- 有什么双关语可以用吗? 这可能是反方最后一个反对意见了。我知道,有人曾经用飞机喷出的尾迹在天空中划出了 \( \pi \) 的数字,然后说“\( \pi \) in the Sky”,它听上去挺押韵,挺酷的。但是 \( \tau \) 却有更多类似的朗朗上口的双关语境,而且寓意更深。道数主义(\( \tau \)-ism)告诉我们说:\( \tau \) 不是从“派”(\( \pi \))里切出去的一块,\( \pi \) 才是 \( \tau \) 的一部分,确切地说它是 \( \tau \) 的一半。欧拉恒等式 \( e^{i\tau} = 1\) 是如此的优美,它似乎直接表述了东方古老文化里道家的理念:正所谓 “道法自然,天人合一”(“Be one with the τ”),以及“千道轮回无始终,万般因果皆归一” (“A rotation by one turn is 1”),这就是“道”(\( \tau \))的真谛。我们在体会“道法自然”这一道家思想的同时也必须谨记,道数主义(\( \tau \)-ism)是理性的产物,而不是建立在虚无信仰之上的空中楼阁。就像这句英文的双关语所说的:\( \tau \)ists (Tau-ist) are never \( \pi \)ous (Pious)。
6.2 推广 Tau 的使用
我们从《Tau 宣言》里看到圆周率的自然定义应该是圆周长除以半径,而不是除以直径。我们要为这个数取一个名字,我希望你能加入我们的行列,用 \( \tau \) 来称呼它:
它用法自然,目标明确,影响深远。而且,它还可以和酷酷的太极图(图 17)相映生辉。我们可以这样来按图索骥:从 0 到 \( \tau/2 \) 是阳在上,代表光明;然后继续从 \( \tau/2 \) 转到 \( \tau \) 是阴在下,代表黑暗;这个过程完成了一个阴阳的轮回24。你可以想象,如果用 \( \pi \) 而不用 \( \tau \) 我们就会陷入一个道家所说的“孤阴不生,独阳不长”的困境。

6.3 Tau Day
《Tau 宣言》最初于 2010 年 6 月 28 日(Tau Day)首次发布,而 Tau Day 也成了一个数学爱好者的欢庆日25。如果你想了解有关 \( \tau \) 的最新动态(包括将来有关 Tau Day 的活动通知),请加入以下《Tau 宣言》的通信录。如果你觉得 Pi Day 的派(Pie)味道不错,你可以再多等一段时间,等 Tau Day 到来的时候不妨再来个双份(double Pies)!
致谢
我首先要感谢 Bob Palais。我已经记不清楚在看到他写的《\( \pi \) 是错误的!》文章之前我对 \( \pi \) 的怀疑已经到了多么深的程度,但是《\( \pi \) 是错误的!》这篇文章绝对让我眼界大开,而且这篇《Tau 宣言》里每一个章节都多多少少受到了他那篇文章的恩惠。在此我要感谢他对这篇宣言给予的建设性的意见和慷慨的支持。
我为《Tau 宣言》构思了很长时间,这篇文章里所呈现的想法有很多是我和我的朋友 Sumit Daftuar 讨论的结果。Sumit 经常扮演我的传声筒和魔鬼代言人的角色,他以一个教师和数学家的洞察力从很多方面引导了我的思路。
我还收到过一些读者的热心鼓励和非常有益的反馈意见。这里我想特别感谢 Vi Hart 和 Michael Blake 所精心制作的为 \( \tau \) 有感而发的视频,还有 Don “Blue” McConnell 和 Skona Brittain 在把 \( \tau \) 带入极客文化上所作的工作(他们分别开发了 time-in-\( \tau \) 和 tau clock,的手机程序)。《Tau 宣言》里对太极图阴阳交替的诠释是 Peter Harremoës 所提出的,而且他也曾经独立提出过用 \( \tau \) 作为圆周率的建议。在《Tau 宣言》发表前就已经很活跃的另一位“道家” Joseph Lindenberg 也是这篇宣言坚定不移的拥护者,我对他给予的的热情支持表示由衷感谢。我也从 Christopher Olah 那里采纳了很多好的建议,特别是对欧拉恒等式的几何诠释部分。还有第 2.3.2 节里欧拉恒等式表是来自 Timothy “Patashu” Stiles 的灵感和建议。Don Blaheta 预料到了用超球体作为论证的重要性,并提供了相关资料,之后由 John Kodegadulo 以其清晰的思路和通俗易懂的方式整理成文。还有 Jeff Cornell 从他独到的眼光注意到了 \( \tau/4 \) 在这个课题里的重要性,我的信仰和认知也因此被彻底颠覆。
最后,我还要感谢 Wyatt Greene 在这篇宣言发布之前对我的初稿提出了很多非常宝贵的反馈意见。他这个人有很多突出的地方, 特别是如果你想找一个人给你讲类似于“你写的第 5 节的内容多半都是垃圾”这样的箴言,Wyatt 将会是一个不二的人选。
版权声明
《Tau 宣言》的版权 © 2010–2018 归作者 Michael Hartl 所有。

