O Manifesto Tau
Michael HartlTraduzido por Gustavo Chaves
Dia do Tau de 2010atualizado no Dia do Tau de 2020
1 A constante do círculo
O Manifesto Tau é dedicado a um dos números mais importantes da matemática, talvez o mais importante: a constante do círculo, que relaciona a circunferência de um círculo à sua dimensão linear. Por milênios o círculo foi considerado a mais perfeita das formas e a constante do círculo captura a sua geometria em um único número. Obviamente, a escolha tradicional para a constante do círculo é \( \pi \) (pi)—mas, como o matemático Bob Palais observa em seu delicioso artigo “\( \pi \) Está Errado!”1, \( \pi \) está errado. E já passou da hora de corrigi-lo.
1.1 Uma proposta imodesta
Começamos a reparar os danos causados por \( \pi \) pela compreenção do seu significado. A definição tradicional da constante do círculo estabelece que \( \pi \) é igual à razão entre a circunferência (comprimento) e o diâmetro (largura) de um círculo:2
O número \( \pi \) tem muitas propriedades notáveis—entre outras, ele é irracional e transcendental—e sua presença em fórmulas matemáticas é generalizada.
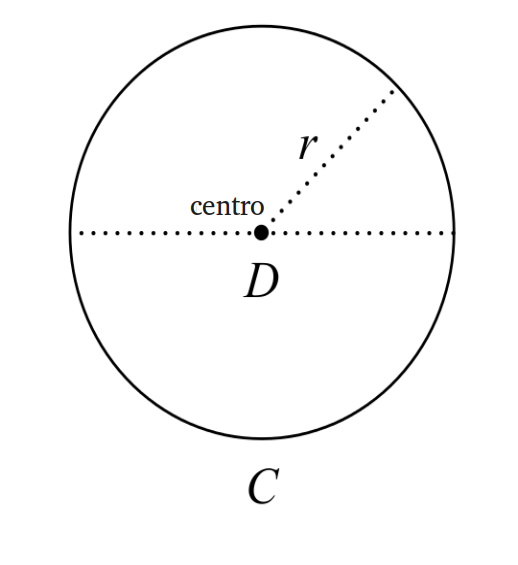
É óbvio que \( \pi \) não está “errado” no sentido de estar factualmente incorreto; o número \( \pi \) é perfeitamente bem definido e possui todas as propriedades normalmente atribuídas a ele pelos matemáticos. Quando dizemos que “\( \pi \) está errado”, queremos dizer que \( \pi \) é uma escolha confusa e pouco natural para a constante do círculo. Em particular, um círculo é definido como o conjunto de pontos a uma distância fixa, o raio, de um determinado ponto, o centro (Figura 1). Embora existam infinitas formas de largura constante (Figura 2)3, há apenas uma forma de raio constante, o que sugere que uma definição mais natural para a constante do círculo deveria usar \( r \) no lugar de \( D \):
Como o diâmetro de um círculo é o dobro do raio, este número é igual a \( 2\pi \). Como \( \pi \), ele é transcendental e, portanto, irracional, e (como veremos na Seção 2), seu uso na matemática é igualmente difundido.
Em “\( \pi \) Está Errado!”, Bob Palais argumenta de forma persuasiva a favor da segunda dessas duas definições para a constante do círculo, e, na minha opinião, ele merece o crédito principal por identificar esse problema e levá-lo a uma ampla audiência. Ele chama a verdadeira constante do círculo de “uma volta” e também introduz um novo símbolo para representá-lo (Figura 3). Como veremos, sua descrição é presciente, no entanto o símbolo sugerido é bastante estranho e (como discutido na Seção 4), parece improvável que obtenha ampla adoção. (Atualização: Isto provou ser realmente o caso, e o próprio Palais se tornou um grande defensor dos argumentos deste manifesto.)

O Manifesto Tau é dedicado à proposição de que a melhor resposta a “\( \pi \) está errado” é “De fato!". E a verdadeira constante do círculo merece um nome adequado. Como você já deve ter adivinhado, O Manifesto Tau propõe que este nome seja a letra grega \( \tau \) (tau):
Ao longo deste manifesto, veremos que o número \( \tau \) é a escolha correta e mostraremos através do uso (Seção 2 e Seção 3) e por argumentação direta (Seção 4) que a letra \( \tau \) também é uma escolha natural.
1.2 Um inimigo poderoso
Antes de prosseguir com a demonstração de que \( \tau \) é a escolha natural para a constante do círculo, vamos primeiro entender o que estamos enfrentando—porque há uma conspiração poderosa, com séculos de idade, determinada a propagar propaganda pró-\( \pi \). Livros inteiros foram escritos exaltando as virtudes de \( \pi \). (Imagine, livros!) E a devoção irracional a \( \pi \) se espalhou até os mais altos escalões da cultura nerd; por exemplo, no “Dia do Pi” de 2010 o Google mudou seu logo para homenagear \( \pi \) (Figure 4).
Enquanto isso, algumas pessoas memorizam dezenas, centenas e até milhares de dígitos desse número místico. Que tipo de gente memoriza até 40 dígitos de \( \pi \) (Figura 5)?4
Certamente, os proponentes do \( \tau \) enfrentam um forte inimigo. E, no entanto, temos um poderoso aliado—pois a verdade está do nosso lado.
2 O número tau
Vimos na Seção 1.1 que o número \( \tau \) também pode ser escrito como \( 2\pi \). Como observado em “\( \pi \) Está Errado!”, é, portanto, de grande interesse descobrir que a combinação \( 2\pi \) ocorre com uma frequência surpreendente em todos os campos da matemática. Por exemplo, considere as integrais espaciais em coordenadas polares:
O limite superior de integração da variável \( \theta \) é sempre \( 2\pi \). O mesmo fator aparece na definição da Distribuição gaussiana (normal),
e, novamente, na transformada de Fourier,
Ela reaparece, também, na fórmula integral de Cauchy,
nas \( n \)-ésimas raízes da unidade,
e nos valores da função zeta de Riemann para inteiros positivos pares:5
Essas fórmulas não foram escolhidas a dedo—abra seu livro favorito de física ou matemática e tente você mesmo. Há muitos outros exemplos e a conclusão é clara: há algo de especial em \( 2\pi \).
Para chegar ao fundo deste mistério devemos retornar aos princípios fundamentais, considerando a natureza dos círculos e, especialmente, a natureza dos ângulos. Embora seja provável que grande parte deste material soe familiar, vale a pena revisitá-lo, pois é neste ponto que o verdadeiro entendimento de \( \tau \) começa.
2.1 Círculos e ângulos
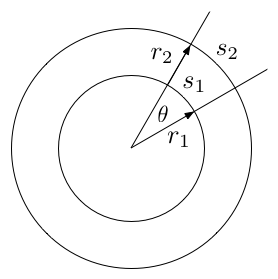
Existe uma relação íntima entre círculos e ângulos, como mostra a Figura 6. Como os círculos concêntricos na Figura 6 têm raios diferentes, as linhas na figura cortam diferentes comprimentos de arco, mas o ângulo \( \theta \) (teta) é o mesmo em cada caso. Em outras palavras, o tamanho do ângulo não depende do raio do círculo usado para definir o arco. A principal tarefa da medição de ângulos é criar um sistema que capte esta invariância com respeito ao raio.
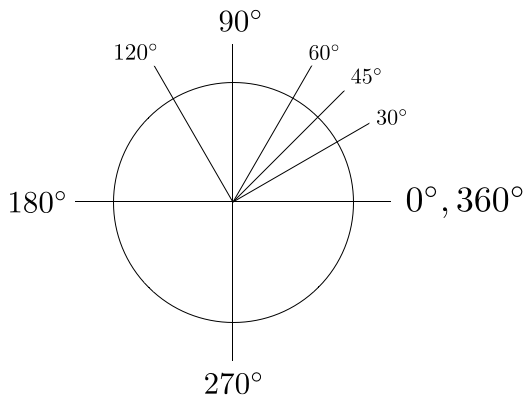
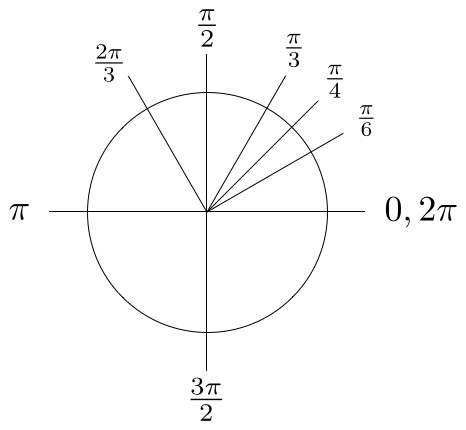
Provavelmente o sistema de ângulos mais simples seja o baseado em graus, que divide um círculo em 360 partes iguais. Um resultado deste sistema é o conjunto de ângulos especiais (familiares aos estudantes de trigonometria) mostrados na Figura 7.
Um sistema mais fundamental de medida de ângulo envolve uma comparação direta entre o comprimento do arco \( s \) e o raio \( r \). Embora os comprimentos na Figura 6 sejam diferentes, o comprimento do arco cresce proporcionalmente ao raio, portanto, a proporção entre o comprimento do arco e o raio é a mesma em cada caso:
Isto sugere a seguinte definição de medida de ângulos em radianos:
Esta definição tem a propriedade desejada de ser invariante em relação ao raio e, uma vez que tanto \( s \) quanto \( r \) têm unidades de comprimento, radianos são adimensionais por construção. O uso da medida do ângulo em radianos leva a fórmulas sucintas e elegantes em toda a matemática; por exemplo, a fórmula usual para a derivada de \( \sen\theta \) é verdadeira somente quando \( \theta \) é expresso em radianos:
Naturalmente, os ângulos especiais na Figura 7 podem ser expressos em radianos e, quando você estudou trigonometria no ensino médio, você provavelmente memorizou os valores especiais mostrados na Figura 8. (Eu chamo esse sistema de medida de \( \pi \)-radianos para enfatizar que eles são escritos em termos de \( \pi \).)
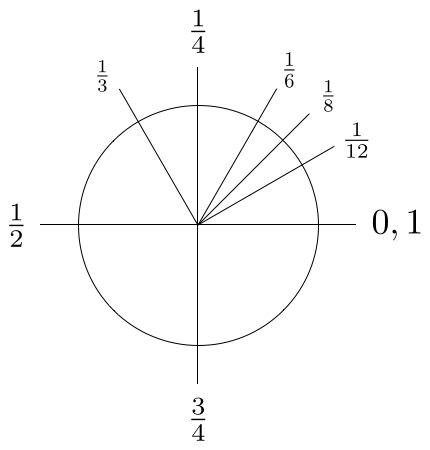
Agora, um momento de reflexão mostra que os, assim chamados, ângulos “especiais”, nada mais são que frações racionais particularmente simples de um círculo completo, como mostra a Figura 9. Isto sugere que devemos revisitar a Eq. (4), reescrevendo o comprimento do arco \( s \) em termos da fração \( f \) da circunferência completa \( C \), ou seja, \( s = f C \):
Observe como \( \tau \) aparece tão naturalmente nesta análise. Se você acredita em \( \pi \), receio que o novo diagrama de ângulos especiais (Figura 10) abale os alicerces da sua fé.
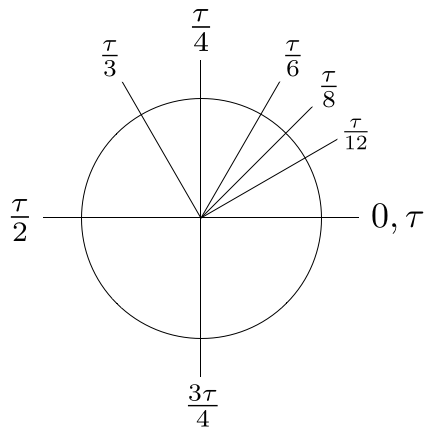
Embora existam muitos outros argumentos em favor de \( \tau \), a Figura 10 deve ser o mais impressionante. Também vemos na Figura 10 a genialidade de Bob Palais ao identificar a constante do círculo como “uma volta”: \( \tau \) é a medida do ângulo em radianos para uma volta de círculo. Além disso, observe que, com \( \tau \) não há nada para memorizar: um doze avos de volta é \( \tau/12 \), um oitavo de volta é \( \tau/8 \) e assim por diante. Usar \( \tau \) nos dá o melhor dos dois mundos, combinando clareza conceitual com todos os benefícios concretos dos radianos; o significado abstrato de, digamos, \( \tau/12 \) é óbvio, mas também é apenas um número:
Finalmente, comparando a Figura 8 com a Figura 10, vemos de onde vêm estes fatores incômodos de \( 2\pi \): uma volta de círculo é \( 1\tau \), mas \( 2\pi \). Numericamente, são iguais, mas conceitualmente são bastante distintos.
As ramificações
Esses fatores desnecessários de \( 2 \) decorrentes do uso de \( \pi \) são irritantes por si só, mas muito mais séria é a sua tendência a se cancelarem quando divididos por qualquer número par. Esses resultados absurdos, como a metade de \( \pi \) para um quarto de volta, ocultam a relação subjacente entre a medida do ângulo e a constante do círculo. Aos que dizem que “não importa” se usamos \( \pi \) ou \( \tau \) quando ensinamos trigonometria, peço apenas que vejam a Figura 8, a Figura 9 e a Figura 10 através dos olhos de uma criança. Vocês verão que, da perspectiva de um iniciante, usar \( \pi \) ao invés de \( \tau \) é um desastre pedagógico.
2.2 As funções do círculo
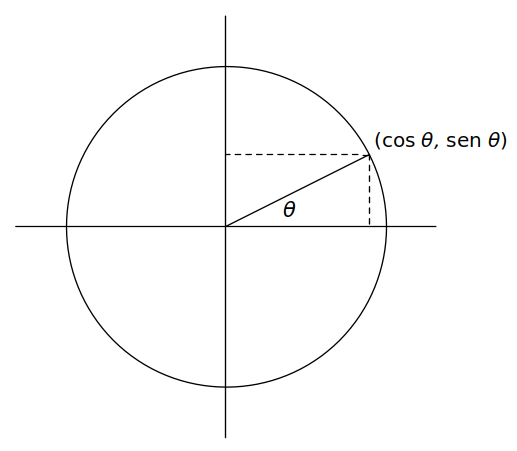
Embora a medida do ângulo radiano forneça alguns dos argumentos mais convincentes para a verdadeira constante do círculo, vale a pena comparar as virtudes de \( \pi \) e \( \tau \) em alguns outros contextos também. Começamos considerando as importantes funções elementares \( \sen\theta \) e \( \cos\theta \). Conhecidas como as “funções do círculo”, porque fornecem as coordenadas de um ponto no círculo unitário (isto é, um círculo com raio \( 1 \)), seno e cosseno são as funções fundamentais da trigonometria (Figura 11).
Vamos examinar os gráficos das funções do círculo para entender melhor o seu comportamento.6 Você verá na Figura 12 e na Figura 13 que as duas funções são periódicas com período \( T \). Como mostra a Figura 12, a função seno \( \sen\theta \) começa em zero, atinge o máximo em um quarto de período, passa pelo zero em meio período, atinge o mínimo em três quartos de período e retorna a zero após um período completo. Enquanto isso, a função cosseno \( \cos\theta \) começa no máximo, tem um mínimo em meio período e passa pelo zero em um quarto e em três quartos de período (Figura 13). Para referência, as duas figuras mostram o valor de \( \theta \) (em radianos) em cada ponto especial.
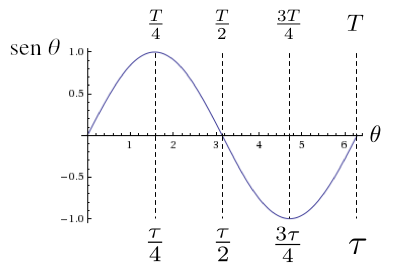
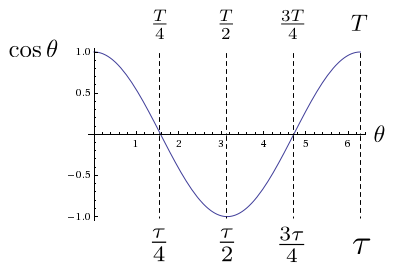
Obviamente, como tanto o seno quanto o cosseno passam por um ciclo completo durante uma volta do círculo, temos que \( T = \tau \); ou seja, as funções do círculo têm períodos iguais à constante do círculo. Como resultado, os valores “especiais” de \( \theta \) são absolutamente naturais: um quarto de período é \( \tau/4 \), meio período é \( \tau/2 \), etc. De fato, ao criar a Figura 12, a certa altura, eu me peguei pensando sobre o valor numérico de \( \theta \) para o zero da função seno. Como o zero ocorre após meio período e como \( \tau \approx 6,28 \), um cálculo mental rápido levou ao seguinte resultado:
É isso mesmo: fiquei surpreso ao descobrir que eu já havia esquecido que \( \tau/2 \) às vezes é chamado de “\( \pi \)”. Talvez isso tenha acontecido com você agora. Bem-vindo ao meu mundo.
2.3 A identidade de Euler
Seria negligente da minha parte não abordar neste manifesto a identidade de Euler, às vezes chamada de “a mais bela equação da matemática”. Essa identidade envolve a exponencial complexa, que está profundamente conectada tanto às funções do círculo quanto à sua própria geometria.
Dependendo do caminho escolhido, a seguinte equação pode ser provada como um teorema ou tomada como uma definição; de qualquer forma, ela é notável:
Conhecida como a fórmula de Euler (em honra a Leonhard Euler), esta equação relaciona uma exponencial com argumento imaginário às funções do círculo seno e cosseno e à unidade imaginária \( i \). Embora justificar a fórmula de Euler esteja além do escopo deste manifesto, sua origem está acima de qualquer suspeita e sua importância é inquestionável.
Avaliando a Eq. (5) em \( \theta = \tau \) obtemos como resultado a identidade de Euler:7
Em palavras, a Eq. (6) faz a seguinte observação fundamental:
A exponencial complexa do círculo é a unidade.
Geometricamente, multiplicar por \( e^{i\theta} \) corresponde à rotação de um número complexo por um ângulo \( \theta \) no plano complexo, o que sugere uma segunda interpretação da identidade de Euler:
Uma rotação de uma volta é 1.
Como o número \( 1 \) é o elemento identidade, o significado geométrico de \( e^{i\tau} = 1 \) é que rodar um ponto no plano complexo uma volta completa simplesmente o leva de volta à sua posição original.
Como no caso da medida de ângulos em radianos, vemos quão natural é a associação entre \( \tau \) e uma volta de círculo. De fato, a identificação de \( \tau \) com “uma volta” faz com que a identidade de Euler soe quase como uma tautologia.8
Não exatamente a equação mais bonita
Obviamente, a forma tradicional da identidade de Euler é escrita em termos de \( \pi \) ao invés de \( \tau \). Para derivá-la, começamos avaliando a fórmula de Euler em \( \theta = \pi \), que resulta em
Mas este sinal de menos é tão feio que a Eq. (7) é quase sempre reorganizada imediatamente, dando lugar à seguinte equação “bonita”:
Neste ponto, o expositor geralmente faz uma declaração grandiosa sobre como a Eq. (8) relaciona \( 0 \), \( 1 \), \( e \), \( i \) e \( \pi \)—às vezes chamados de os “cinco números mais importantes da matemática”.
Neste contexto, é notável quantas pessoas se queixam de que a Eq. (6) relaciona apenas quatro daqueles cinco. Bem:
A Eq. (9), sem reorganização, na verdade relaciona os cinco números mais importantes da matemática: \( 0 \), \( 1 \), \( e \), \( i \) e \( \tau \).9
Identidades eulerianas
Como você pode adicionar zero em qualquer lugar de qualquer equação, a introdução de \( 0 \) na Eq. (9) é um contraponto um tanto irônico a \( e^{i\pi} + 1 = 0 \), mas a identidade \( e^{i\pi} = -1 \) tem algo sério a dizer. Vejamos o que acontece quando a reescrevemos em termos de \( \tau \):
Geometricamente, isto diz que uma rotação de meia volta é o mesmo que multiplicar por \( -1 \). E, de fato, é este o caso: quando rotacionado \( \tau/2 \) radianos, o número complexo \( z = a + ib \) é mapeado para \( -a - ib \), que é de fato apenas \( -1\cdot z \).
Escrita em termos de \( \tau \), vemos que a forma “original” da identidade de Euler (Eq. (7)) tem um significado geométrico transparente que faz falta quando escrita em termos de \( \pi \). (Obviamente, \( e^{i\pi} = -1 \) pode ser interpretado como uma rotação de \( \pi \) radianos, mas a reorganização quase universal para formar \( e^{i\pi} + 1 = 0 \) mostra como usar \( \pi \) desvia a atenção do significado geométrico natural da identidade.) As identidades de quarto de ângulo têm interpretações geométricas similares: avaliando a Eq. (5) em \( \tau/4 \) dá \( e^{i\tau/4} = i \), que significa que um quarto de volta no plano complexo é o mesmo que multiplicar por \( i \); similarmente, \( e^{i\cdot(3\tau/4)} = -i \) significa que três quartos de volta é o mesmo que multiplicar por \( -i \). Um resumo destes resultados, que chamaremos de identidades eulerianas, aparece na Tabela 1.
| Ângulo de rotação | Identidade euleriana | ||
| \( 0 \) | \( e^{i\cdot0} \) | \( = \) | \( 1 \) |
| \( \tau/4 \) | \( e^{i\tau/4} \) | \( = \) | \( i \) |
| \( \tau/2 \) | \( e^{i\tau/2} \) | \( = \) | \( -1 \) |
| \( 3\tau/4 \) | \( e^{i\cdot(3\tau/4)} \) | \( = \) | \( -i \) |
| \( \tau \) | \( e^{i\tau} \) | \( = \) | \( 1 \) |
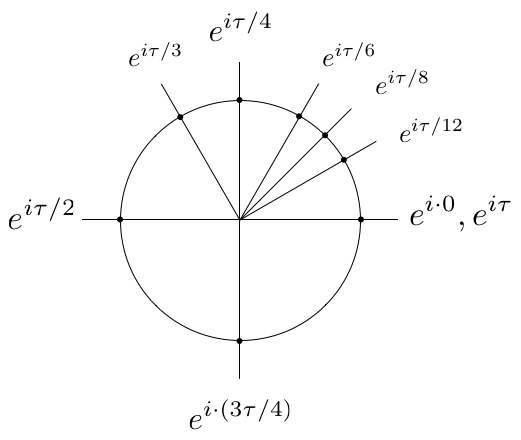
Podemos levar esta análise um passo adiante observando que, para qualquer ângulo \( \theta \), \( e^{i\theta} \) pode ser interpretado como um ponto localizado no círculo unitário no plano complexo. Como o plano complexo identifica o eixo horizontal com a parte real do número e o eixo vertical com a parte imaginária, a fórmula de Euler nos diz que \( e^{i\theta} \) corresponde às coordenadas \( (\cos\theta, \sen\theta) \). Substituindo os valores dos ângulos “especiais” da Figura 10 na Eq. (5) fornece, então, os pontos mostrados na Tabela 2 e, plotando esses pontos no plano complexo, produz a Figura 14. Uma comparação da Figura 14 com a Figura 10 imediatamente elimina quaisquer dúvidas sobre qual opção de constante do círculo revela melhor a relação entre a fórmula de Euler e a geometria do círculo.
| Forma polar | Forma Retangular | Coordenadas |
| \( e^{i\theta} \) | \( \cos\theta + i\sen\theta \) | \( (\cos\theta, \sen\theta) \) |
| \( e^{i\cdot0} \) | \( 1 \) | \( (1, 0) \) |
| \( e^{i\tau/12} \) | \( \frac{\sqrt{3}}{2} + \frac{1}{2}i \) | \( (\frac{\sqrt{3}}{2}, \frac{1}{2}) \) |
| \( e^{i\tau/8} \) | \( \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i \) | \( (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) \) |
| \( e^{i\tau/6} \) | \( \frac{1}{2} +\frac{\sqrt{3}}{2} i \) | \( (\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( e^{i\tau/4} \) | \( i \) | \( (0, 1) \) |
| \( e^{i\tau/3} \) | \( -\frac{1}{2} +\frac{\sqrt{3}}{2} i \) | \( (-\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( e^{i\tau/2} \) | \( -1 \) | \( (-1, 0) \) |
| \( e^{i\cdot(3\tau/4)} \) | \( -i \) | \( (0, -1) \) |
| \( e^{i\tau} \) | \( 1 \) | \( (1, 0) \) |
3 Área circular: o golpe de misericórdia
Se você chegou até aqui como um crente em \( \pi \), agoravocê já deve estar questionando a sua fé. \( \tau \) é tão natural, seu significado é tão transparente—será que não há um exemplo em que \( \pi \) brilha em toda a sua glória radiante? Uma memória se agita—sim, existe uma fórmula—a fórmula para a área circular! Contemple-a:
Espere um pouco. A fórmula da área é sempre escrita em termos do raio, assim:
Vemos aqui \( \pi \), sem adornos, em uma das equações mais importantes da matemática—uma fórmula provada pela primeira vez pelo próprio Arquimedes. A ordem foi restaurada! E, no entanto, o nome desta seção parece ameaçador… Se esta equação for a coroação gloriosa de \( \pi \), como pode ser também o golpe de misericórdia?
3.1 Formas quadráticas
Examinemos este modelo exemplar de \( \pi \), \( A = \pi r^2 \). Percebemos que ele envolve o diâmetro—não, espere, o raio—elevado à segunda potência. Isso faz dele uma forma quadrática simples. Tais formas surgem em muitos contextos; como um físico, meus exemplos favoritos vêm do currículo básico de física. Vamos considerá-los um de cada vez.
Queda em um campo gravitacional uniforme
Galileu Galilei descobriu que a velocidade de um objeto que cai em um campo gravitacional uniforme é proporcional ao tempo de queda:
A constante de proporcionalidade é a aceleração gravitacional \( g \):
Como a velocidade é a derivada da posição, podemos calcular a distância da queda por integração:10
Energia potencial em uma mola linear
Robert Hooke descobriu que a força externa necessária para esticar uma mola é proporcional à distância esticada:
A constante de proporcionalidade é a constante da mola \( k \):11
A energia potencial na mola é, então, igual ao trabalho realizado pela força externa:
Energia do movimento
Isaac Newton descobriu que a força em um objeto é proporcional à sua aceleração:
A constante de proporcionalidade é a massa \( m \):
A energia do movimento, ou energia cinética, é igual ao trabalho total realizado ao acelerar a massa até a velocidade \( v \):
3.2 Um pressentimento
Tendo visto vários exemplos de formas quadráticas simples na física, você pode agora ter uma sensação de pressentimento quando retornarmos à geometria do círculo. Esse sentimento é justificado.
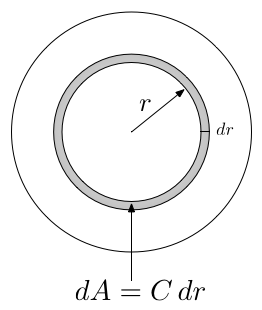
Como visto na Figura 15, a área de um círculo pode ser calculada dividindo-a em anéis circulares de comprimento \( C \) e largura \( dr \), onde a área de cada anel é \( C\,dr \):
Agora, a circunferência de um círculo é proporcional ao seu raio:
A constante de proporcionalidade é \( \tau \):
A área do círculo é, então, a integral sobre todos os anéis:
Se você ainda era um partidário de \( \pi \) no início desta seção, sua cabeça agora explodiu. Pois vemos que, mesmo neste caso, onde \( \pi \) supostamente brilha, de fato há um fator de \( 2 \) ausente. Com efeito, a prova original de Arquimedes não mostra que a área de um círculo é \( \pi r^2 \), mas que é igual à área de um triângulo retângulo com base \( C \) e altura \( r \). A aplicação da fórmula para a área triangular fornece, então
Simplesmente não há como evitar este fator de um meio (Tabela 3).
| Quantidade | Símbolo | Expressão |
| Distância de queda | \( y \) | \( \textstyle{\frac{1}{2}}gt^2 \) |
| Energia da mola | \( U \) | \( \textstyle{\frac{1}{2}}kx^2 \) |
| Energia cinética | \( K \) | \( \textstyle{\frac{1}{2}}mv^2 \) |
| Área do círculo | \( A \) | \( \textstyle{\frac{1}{2}}\tau\,r^2 \) |
Quod erat demonstrandum
Neste manifesto nós nos propusemos a mostrar que \( \tau \) é a verdadeira constante do círculo. Como a fórmula para a área do círculo era praticamente o último e o melhor argumento que \( \pi \) tinha a seu favor, eu irei contra a corrente aqui e direi: Q.E.D.
4 Conflito e resistência
Apesar da demonstração definitiva da superioridade de \( \tau \), ainda há muitos que se opõem a ele, tanto como notação quanto como número. Nesta seção, abordamos as preocupações daqueles que aceitam o valor, mas não a letra. Em seguida, refutamos alguns dos muitos argumentos reunidos contra \( C/r \) em si, incluindo o chamado “Manifesto Pi” que defende a primazia de \( \pi \). Neste contexto, discutiremos o assunto bastante avançado do volume de uma hiperesfera (Seção 5.1), que melhora e amplia os argumentos da Seção 3 sobre a área do círculo.
4.1 Uma volta
O verdadeiro teste de qualquer notação é o uso; tendo visto \( \tau \) ser usado ao longo deste manifesto, você já deve estar convencido de que ele desempenha bem seu papel. Mas para uma constante tão fundamental quanto \( \tau \) seria bom termos algumas razões mais profundas para a nossa escolha. Por que não \( \alpha \), por exemplo, ou \( \omega \)? O que há de tão especial sobre o \( \tau \)?
Há duas razões principais para usar \( \tau \) como a constante do círculo. A primeira é que \( \tau \) se assemelha visualmente a \( \pi \): após séculos de uso, a associação de \( \pi \) com a constante do círculo é inevitável, e usar \( \tau \) se aproveita desta associação em vez de combatê-la. (De fato, a linha horizontal em cada letra sugere que interpretemos as “pernas” como denominadores, de modo que \( \pi \) tem duas pernas em seu denominador, enquanto \( \tau \) tem apenas uma. Visto desta maneira, a relação \( \tau = 2\pi \) é perfeitamente natural.)12
A segunda razão é que \( \tau \) corresponde a uma volta, ou um torno, de círculo e você deve ter percebido que tanto “\( \tau \)” quanto “torno” começam com um som “t”. Esta foi a motivação original para a escolha de \( \tau \) e não é mera coincidência: a raiz da palavra “torno” é a palavra grega τόρνος (tornos). Usar uma fonte matemática para a primeira letra em τόρνος nos dá: \( \tau \).
Depois do lançamento original de O Manifesto Tau, eu descobri que Peter Harremoës propôs independentemente, em 2010, o uso de \( \tau \) para Bob Palais, autor de “\( \pi \) Está Errado!”, que John Fisher propôs \( \tau \), em 2004, em um post da Usenet e que Joseph Lindenberg antecipou tanto o argumento quanto o símbolo mais de vinte anos antes!13 O Dr. Harremoës, em particular, enfatizou a importância de uma observação feita na Seção 1.1: usar \( \tau \) dá à contante do círculo um nome. Como \( \tau \) é uma letra grega comum, as pessoas que a encontram pela primeira vez podem pronunciá-la imediatamente. Além disso, diferentemente de “uma volta”, chamar a constante do círculo de \( \tau \) funciona bem em contextos escritos e falados. Por exemplo, dizer que um quarto de círculo mede “um quarto de volta” em radianos parece ótimo, mas “dar quatro radianos de volta” soa estranho e “a área de um círculo é meia volta \( r \) ao quadrado” soa absolutamente bizarro. Usando \( \tau \), podemos dizer “tau sobre quatro radianos” e “a área de um círculo é meio tau \( r \) ao quadrado”.
Notação Ambígua
Obviamente, com qualquer nova notação, existe o potencial de conflito com o uso corrente. Conforme observado na Seção 1.1, “\( \pi \) Está Errado!” evita esse problema introduzindo um novo símbolo (Figura 3). Há precedentes para isso; por exemplo, nos primórdios da mecânica quântica, Max Planck introduziu a constante \( h \), que relaciona a energia de uma partícula de luz à sua frequência (através de \( E = h\nu \)), mas os físicos logo perceberam que é com frequência é mais conveniente usar \( \hbar \) (leia-se “h-barra”)—onde \( \hbar \) não é nada mais que \( h \) dividido por… hum… \( 2\pi \)—e esse uso agora é padrão.
Porém, fazer um novo símbolo ser aceito é difícil: ele precisa de um nome, esse nome deve ser popularizado e o próprio símbolo deve ser adicionado aos sistemas de processamento de texto e de tipografia. Além disso, promulgar um novo símbolo para \( 2\pi \) exigiria a cooperação da comunidade acadêmica matemática, a qual em matéria de \( \pi \) vs. \( \tau \) tem sido, até agora, apática na melhor das hipóteses e hostil na pior delas. Usar um símbolo existente ajuda a vencer essa resistência.14
Em vez de advogar um novo símbolo, O Manifesto Tau opta por usar uma letra grega existente. Deste modo, como \( \tau \) já é usado em outros contextos, precisamos resolver os conflitos com a prática atual. Felizmente, há poucos casos de uso comum. Além disso, enquanto \( \tau \) é usado para algumas variáveis específicas—por exemplo, tensão de cisalhamento na engenharia mecânica, torque na mecânica rotacional e tempo próprio nas relatividades especial e geral—não há uso universal conflitante.15 Nestes casos, podemos tolerar a ambiguidade ou contornar os poucos conflitos existentes, alterando seletivamente a notação, como usar \( N \) como torque16 ou \( \tau_p \) como tempo próprio.
Apesar destes argumentos, potenciais conflitos de uso provaram ser a maior fonte de resistência ao \( \tau \). Alguns correspondentes chegam a negar categoricamente que \( \tau \) (ou, presumivelmente, qualquer outro símbolo atualmente em uso) poderia superar esses problemas. Mas cientistas e engenheiros são altamente tolerantes à ambiguidade notacional de modo que alegar que \( \tau \)-a-constante-do-círculo não possa coexistir com outros usos ignora muitas evidências em contrário.
Um exemplo de ambiguidade facilmente tolerada ocorre na mecânica quântica, onde encontramos a seguinte fórmula para o raio de Bohr, que (grosso modo) é o “tamanho” de um átomo de hidrogênio em seu estado de energia mais baixo (o estado fundamental):
onde \( m \) é a massa de um elétron e \( e \) é a sua carga. Enquanto isso, o próprio estado fundamental é descrito por uma quantidade conhecida como função de onda, que cai exponencialmente com o raio em uma escala de comprimento definida pelo raio de Bohr:
onde \( N \) é uma constante de normalização.
Percebeu o problema? Provavelmente não, e é exatamente este o ponto. O “problema” é que o \( e \) no raio de Bohr e o \( e \) na função de onda não são o mesmo \( e \)—o primeiro é a carga de um elétron, enquanto o segundo é o número natural (a base dos logaritmos naturais). De fato, se expandirmos o fator de \( a_0 \) no argumento do expoente na Eq. (10), obtemos
que tem um \( e \) elevado à potência de uma expressão contendo \( e \). É ainda pior do que parece, porque o próprio \( N \) também contém \( e \):
Não há dúvidas de que, se uma notação específica para o número natural ainda não existisse, qualquer um que propusesse a letra \( e \) ouviria que é uma sugestão impossível devido aos conflitos com outros usos da letra já em voga. E, no entanto, na prática, ninguém nunca teve nenhum problema em usar \( e \) nos dois contextos acima. Há muitos outros exemplos, incluindo situações em que até \( \pi \) é usado para duas coisas diferentes.17 É difícil entender em que usar \( \tau \) seria diferente para denotar múltiplas quantidades.
A propósito, o \( \pi \)-pedantes por aí (e há muitos) podem notar que a função de onda no estado fundamental do hidrogênio tem um fator de \( \pi \):
À primeira vista, isso parece ser mais natural do que a versão com \( \tau \):
Como sempre, as aparências enganam: o valor de \( N \) vem do produto
que mostra que a constante do círculo entra no cálculo através de \( 1/\sqrt{2\pi} \), ou seja, \( 1/\sqrt{\tau} \). Tal como acontece com a fórmula da área do círculo, o fato de o cancelamento deixar um \( \pi \) isolado não passa de mera coincidência.
4.2 O Manifesto Pi
Embora a maioria das objeções a \( \tau \) venham de correspondência via email e de comentários diversos na Web, há também uma resistência organizada. Em particular, desde a publicação de O Manifesto Tau, em junho de 2010, um “O Manifesto Pi” surgiu para argumentar a favor da constante do círculo tradicional. Esta seção e as duas seguintes contêm uma refutação de seus argumentos. Por necessidade, o tratamento aqui é mais sucinto e mais avançado do que no restante do manifesto, mas mesmo uma leitura superficial do que se segue dará uma impressão da fraqueza do argumento de O Manifesto Pi.
Embora possamos certamente considerar o surgimento de O Manifesto Pi como um bom sinal do interesse contínuo neste assunto, ele faz várias alegações falsas. Por exemplo, ele diz que o fator de \( 2\pi \) na distribuição gaussiana (normal) é uma coincidência e que ela pode ser escrita mais naturalmente como
Isto é errado: o fator de \( 2\pi \) resulta da elevação ao quadrado da distribuição gaussiana não normalizada e da conversão para coordenadas polares, o que leva a um fator de \( 1 \) a partir da integral radial e a \( 2\pi \) a partir da integral angular. Como no caso da área do círculo, o fator de \( \pi \) vem de \( 1/2\times 2\pi \), não de \( \pi \) sozinho.
Uma alegação relacionada é que a função Gamma avaliada em \( 1/2 \) é mais natural em termos de \( \pi \):
onde
Mas \( \Gamma(\frac{1}{2}) \) se reduz para a mesma integral gaussiana como na distribuição normal (ao definir \( u = x^{1/2} \)), de modo que o \( \pi \) neste caso também é realmente \( 1/2\times 2\pi \). De fato, em muitos dos casos citados em O Manifesto Pi, a constante do círculo entra através de uma integral sobre todos os ângulos, ou seja, \( \theta \) varia de \( 0 \) a \( \tau \).
O Manifesto Pi também examina algumas fórmulas para polígonos regulares de \( n \) lados (“\( n \)-gonos”). Por exemplo, ele observa que a soma dos ângulos internos de um \( n \)-gono é dada por
Este problema foi tratado em “\( \pi \) Está Errado!”, que observa o seguinte: “A soma dos ângulos internos [de um triângulo] é \( \pi \), concedido. Mas a soma dos ângulos externos de qualquer polígono, a partir da qual a soma dos ângulos interiores pode ser facilmente derivada, e que se generaliza à integral da curvatura de uma simples curva fechada, é \( 2\pi \).” Além disso, O Manifesto Pi oferece a fórmula para a área de um \( n \)-gono com raio unitário (a distância do centro ao vértice),
chamando-a de “claramente… outra vitória para \( \pi \).” Mas usando a identidade de ângulo duplo \( \sen\theta\cos\theta = \frac{1}{2} \sen 2\theta \) mostra que isso pode ser reescrito como
que é apenas
Em outras palavras, a área de um \( n \)-gono possui um fator natural de \( 1/2 \). De fato, tomando o limite da Eq. (12) como \( n\rightarrow \infty \) (e aplicando a regra de L’Hôpital) dá a área de um polígono regular unitário com infinitos lados, ou seja, um círculo unitário:
Neste contexto, devemos observar que O Manifesto Pi faz muito barulho sobre \( \pi \) ser a área de um disco unitário, de modo que (por exemplo) a área de um quarto de círculo (unitário) é \( \pi/4 \). Alega-se que isso seja um argumento tão bom para \( \pi \) quanto a medida do ângulo em radianos o é para \( \tau \). Infelizmente, para este argumento, conforme observado na Seção 3 e como visto novamente na Eq. (13), o fator de \( 1/2 \) surge naturalmente no contexto da área do círculo. De fato, a fórmula para a área de um setor circular subtendida por ângulo \( \theta \) é
de modo que não há como evitar o fator de \( 1/2 \) em geral. (Vemos assim que \( A = \frac{1}{2} \tau\, r^2 \) é simplesmente o caso especial quando \( \theta = \tau \).)
Em resumo, a diferença entre a medida do ângulo e a área não é arbitrária. Não há fator natural de \( 1/2 \) no caso da medida do ângulo. Por outro lado, no caso da área, o fator de \( 1/2 \) surge através da integral de uma função linear em associação com uma forma quadrática simples. De fato, o argumento em favor de \( \pi \) é ainda pior do que parece, conforme mostrado na próxima seção.
5 Chegando ao fundo de pi e tau
Não paro de me impressionar com a riqueza deste assunto e meu entendimento de \( \pi \) e \( \tau \) evolui continuamente. No Dia do Meio Tau de 2012, eu acreditei ter identificado exatamente o que havia de errado com \( \pi \). Meu argumento baseava-se em uma análise da área de superfície e do volume de uma esfera \( n \)-dimensional, que (como mostrado abaixo) deixa claro que \( \pi \) não tem nenhum significado geométrico fundamental. Contudo, minha análise estava incompleta—um fato que chamou minha atenção em uma mensagem notável de Jeff Cornell, leitor de O Manifesto Tau. Como resultado, esta seção é uma tentativa não apenas de desacreditar definitivamente \( \pi \), mas também de articular a verdade sobre \( \tau \), uma verdade mais profunda e mais sutil do que eu imaginava.
Nota: Esta seção é mais avançada que o restante do manifesto e pode ser ignorada sem perda de continuidade. Se você a achar confusa, recomendo prosseguir diretamente para a conclusão na Seção 6.
5.1 Área superficial e volume de uma hiperesfera
Iniciamos nossas investigações com a generalização de um círculo para dimensões arbitrárias.18 Este objeto, chamado hiperesfera ou uma \( n \)-esfera, pode ser definido da seguinte maneira.19 (Por conveniência, assumimos que estas esferas estão centradas na origem.) Uma \( 0 \)-esfera é o conjunto vazio e definimos o seu “interior” como sendo um ponto.20 Uma \( 1 \)-esfera é o conjunto de todos os pontos que satisfazem
que consiste nos dois pontos \( \pm r \). Seu interior, que satisfaz
é o segmento de linha de \( -r \) a \( r \). Uma \( 2 \)-esfera é um círculo, que é o conjunto de todos os pontos que satisfazem
Seu interior, que satisfaz,
é um disco. Da mesma forma, uma \( 3 \)-esfera satisfaz
e seu interior é uma bola. A generalização para \( n \)-arbitrário, embora difícil de visualizar para \( n > 3 \), é direta: uma \( n \)-esfera é o conjunto de todos os pontos que satisfazem
O Manifesto Pi (discutido na Seção 4.2) inclui uma fórmula para o volume de uma \( n \)-esfera unitária como argumento a favor de \( \pi \):
onde a função Gamma é dada pela Eq. (11). A Eq. (14) é um caso especial da fórmula para um raio qualquer, que também é tipicamente escrita em termos de \( \pi \):
Como \( V_n(r) = \int S_n(r)\,dr \), temos que \( S_n(r) = dV_n(r)/dr \), o que significa que a área da superfície pode ser escrita da seguinte maneira:
Em vez de simplesmente aceitar estas fórmulas sem mais nem menos, vamos ver se podemos destrinchá-las para esclarecer melhor a questão de \( \pi \) vs. \( \tau \). Começamos nossa análise observando que a aparente simplicidade das fórmulas acima é ilusória: embora a função Gama seja notacionalmente simples, na verdade ela é uma integral sobre um domínio semi-infinito, o que não é de modo algum uma idéia simples. Felizmente, a função Gamma pode ser simplificada em certos casos especiais. Por exemplo, quando \( n \) é um número inteiro, é fácil mostrar (usando integração por partes) que
Visto desta maneira, \( \Gamma \) pode ser interpretada como uma generalização da função fatorial para argumentos reais.21
Nas fórmulas para a área superficial e o volume de esferas \( n \)-domensionais, o argumento de \( \Gamma \) não é necessariamente um número inteiro, mas \( \left(1 + \frac{n}{2}\right) \), que é um número inteiro quando \( n \) é par e é um meio-inteiro quando \( n \) é ímpar. Levando isso em conta nos leva à seguinte expressão, que é tirada de uma referência padrão, Wolfram MathWorld, e, como de costume, é escrita em termos de \( \pi \):
Integrando com relação a \( r \) leva a
Vamos examinar a Eq. (18) em mais detalhes. Observe primeiro que o MathWorld usa a função fatorial dupla \( n!! \)—mas, estranhamente, ele o usa apenas nos casos ímpares. (Este é um sinal do que está por vir.) A função fatorial dupla, embora raramente encontrada na matemática, é elementar: é como a função fatorial normal, mas envolve subtrair de \( 2 \) em \( 2 \) em vez de de \( 1 \) em \( 1 \), de modo que, por exemplo, \( 5!! = 5 \cdot 3 \cdot 1 \) e \( 6!! = 6 \cdot 4 \cdot 2 \). Em geral, temos
(Por definição, \( 0!! = 1!! = 1 \).) Observe que a Eq. (19) se divide naturalmente em casos pares e ímpares, tornando a decisão do MathWorld de usá-lo apenas nos casos ímpares ainda mais misteriosa.
Para resolver este mistério, começaremos examinando mais de perto a fórmula para números ímpares \( n \) na Eq. (18):
Ao examinar a expressão
notamos que ela pode ser reescrita como
e aqui reconhecemos nosso velho amigo \( 2\pi \).
Agora vejamos o caso par na Eq. (18). Observamos acima como é estranho usar o fatorial comum no caso par, mas o duplo fatorial no caso ímpar. De fato, como o duplo fatorial já é definido por partes, se unificarmos as fórmulas usando \( n!! \) em ambos os casos, poderíamos retirá-lo como um fator comum:
Então, existe alguma conexão entre o fatorial e o duplo fatorial? Sim—quando \( n \) é par, os dois estão relacionados pela seguinte identidade:
(Isso é fácil de verificar usando indução matemática.) Substituindo isto na fórmula do volume para \( n \) par produz então
que tem uma semelhança impressionante com
e novamente encontramos um fator de \( 2\pi \).
Juntando estes resultados, vemos que a Eq. (18) pode ser reescrita como
e a Eq. (17) pode ser reescrita como
Substituindo \( \tau=2\pi \) na Eq. (21) produz então
Para unificar ainda mais as fórmulas, podemos usar a função piso \( \lfloor x \rfloor \), que é simplesmente o maior número inteiro menor ou igual a \( x \) (equivalente a cortar a parte fracionária, de modo que, por exemplo, \( \lfloor 3,7 \rfloor = \lfloor 3,2 \rfloor = 3 \)). Isto leva a
que nos permite escrever a fórmula da seguinte maneira:
Integrando a Eq. (22) em relação a \( r \) então produz
Lambda
As fórmulas nas Eq. (22) e Eq. (23) representam uma grande melhoria em relação às formulações originais (Eq. (17) e Eq. (18)) em termos de \( \pi \). Mas ainda é possível uma simplificação adicional, usando a medida de um ângulo reto:22
Como veremos na Seção 5.2, a Eq. (24) pode ser reescrita de maneira mais natural em termos das simetrias do círculo:
onde o fator de \( 2^2 \) vem de \( 2^2 \) arcos circulares congruentes (um em cada quadrante) no espaço bidimensional.
A maior vantagem de \( \lambda \) é que ele unifica completamente os casos pares e ímpares nas Eq. (22) e Eq. (23), cada uma das quais tem um fator de \( \tau^{\left\lfloor \frac{n}{2} \right\rfloor} \). Substituindo na Eq. (25) então leva a
Isso significa que podemos reescrever o produto
como
o que elimina a dependência explícita da paridade. Aplicando a Eq. (26) nas Eq. (22) e Eq. (23) dá então
e
A simplificação nas Eq. (27) e Eq. (28) parece vir às custas de um fator de \( 2^n \), mas mesmo isto tem um significado geométrico claro: uma esfera em \( n \) dimensões se divide naturalmente em \( 2^n \) partes congruentes, correspondendo às \( 2^n \) famílias de soluções de \( \sum_{i=1}^{n} x_i^2 = r^2 \) (uma para cada escolha de \( \pm x_i \)). Em duas dimensões, estes são os arcos circulares em cada um dos quatro quadrantes; em três dimensões, são os setores da esfera em cada octante; e assim por diante em dimensões mais altas. Em outras palavras, podemos explorar a simetria da esfera calculando a área de superfície ou o volume de uma parte—tipicamente a parte principal onde \( x_i > 0 \) para cada \( i \)—e, então, encontrar o valor total multiplicando por \( 2^n \).
Que eu saiba, as Eq. (27) e Eq. (28) são as formulações mais simples possíveis da área de superfície esférica e das fórmulas de volume (e, de fato, são as únicas formas que eu fui capaz de memorizar). Considere, particularmente, a fórmula do volume: ao contrário da falsa simplicidade da Eq. (15), a Eq. (28) não envolve integrais extravagantes—apenas as, um tanto exóticas mas elementares, funções piso e duplo fatorial. O volume de uma \( n \)-esfera unitária é meramente o volume de cada parte simétrica, \( \lambda^{\left\lfloor \frac{n}{2} \right\rfloor}/n!! \), multiplicado pelo número de partes, \( 2^n \).
Recorrências
Já vimos, através das Eq. (27) e Eq. (28), que as fórmulas da área superficial e do volume são mais simples em termos do ângulo reto \( \lambda \). No entanto, ainda não esgotamos \( \tau \).
Como vimos na Eq. (28), a fórmula do volume se divide naturalmente em duas famílias, correspondendo a espaços de dimensões pares e ímpares, respectivamente. Isso significa que o volume quadridimensional, \( V_4 \), está relacionado de modo simples a \( V_2 \) mas não a \( V_3 \), enquanto \( V_3 \) está relacionado a \( V_1 \) mas não a \( V_2 \). Qual é exatamente esta relação?
Podemos encontrar a resposta derivando as relações de recorrência entre dimensões.23 Em particular, vamos dividir o volume de uma esfera \( n \)-dimensional pelo volume de uma esfera \( (n-2) \)-dimensional:
Vemos da Eq. (29) que podemos obter o volume de uma \( n \)-esfera simplesmente multiplicando a fórmula para uma \( (n-2) \)-esfera por \( r^2 \) (um fator exigido pela análise dimensional), dividindo por \( n \) e multiplicando pela “constante de recorrência” \( 2^2\lambda \).
Da mesma forma, para a área de superfície, temos
com a mesma constante de recorrência \( 2^2\lambda \).
Assim, em ambas as Eq. (29) e Eq. (30), a constante que relaciona as diferentes dimensões não é \( \lambda \) propriamente, mas a combinação \( 2^2\lambda \). Comparando com a Eq. (25), vemos que este não é outro que não o \( \tau \)! De fato, uma derivação alternativa da recorrência do volume por cálculo direto (que usa \( R \) onde escrevemos \( r \)) conclui com a integral
mostrando assim que a identificação de \( \tau \) como a “constante de recorrência” não é uma coincidência—a constante de recorrência e a constante do círculo são realmente as mesmas:
Como resultado, é \( tau \), não \( \lambda \), que fornece o fio comum que une as duas famílias de soluções pares e ímpares, conforme ilustrado por Joseph Lindenberg em Tau Before It Was Cool (Figura 16).24
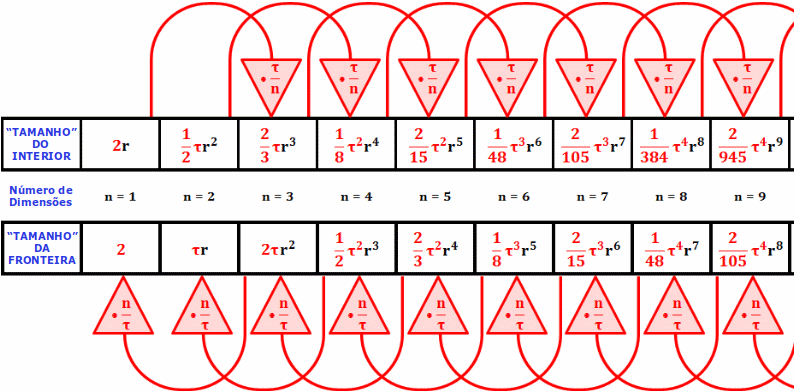
Ao discutir esferas \( n \)-dimensionais em geral, por conveniência, escreveremos as fórmulas da área de superfície e de volume em termos de \( \lambda \) como nas Eq. (27) e Eq. (28), mas para um \( n \) qualquer expressaremos os resultados em termos da constante de recorrência \( \tau \).
5.2 Três famílias de constantes
Equipado com as ferramentas desenvolvidas na Seção 5.1, estamos prontos agora para chegar ao fundo da questão sobre \( \pi \) e \( \tau \). Para concluir a escavação, usaremos as Eq. (27) e Eq. (28) para definir duas famílias de constantes e, em seguida, usar a definição de \( \pi \) (Eq. (1)) para definir uma terceira, revelando assim exatamente o que há de errado com \( \pi \).
Primeiro, definiremos uma família de “constantes da área de superfície” \( \tau_n \) dividindo a Eq. (27) por \( r^{n-1} \), a potência de \( r \) necessária para produzir uma constante adimensional para cada valor de \( n \):
Segundo, definiremos uma família de “constantes de volume” \( \sigma_n \) dividindo a fórmula do volume Eq. (28) por \( r^n \), produzindo novamente uma constante adimensional para cada valor de \( n \):
Com as duas famílias de constantes definidas pelas Eq. (32) e Eq. (33), podemos escrever as fórmulas da área de superfície e do volume (Eq. (27) and Eq. (28)) de modo compacto da seguinte forma:
e
Por conta da relação \( V_n(r) = \int S_n(r)\,dr \), temos a seguinte relação simples
Vamos fazer algumas observações sobre essas duas famílias de constantes. A família \( \tau_n \) tem um significado geométrico importante: fazendo \( r=1 \) na Eq. (32), vemos que cada \( \tau_n \) é a área de superfície de uma \( n \)-esfera unitária, que também é a medida do ângulo de uma \( n \)-esfera completa. Em particular, escrevendo \( s_n(r) \) como o “comprimento de arco” \( n \)-dimensional correspondente a uma fração \( f \) da área total da superfície \( S_n(r) \), temos
Aqui \( \theta_n \) é simplesmente a generalização \( n \)-dimensional da medida do ângulo radiano, e vemos que \( \tau_n \) é a generalização de “uma volta” para \( n \) dimensões, o que explica por que a constante \( \tau_2 = 2^2\lambda = \tau \) da 2-esfera (círculo) leva naturalmente ao diagrama mostrado na Figura 10. Além disso, aprendemos na Seção 5.1 que \( \tau_2 \) também é a “constante de recorrência” para áreas de superfície e volumes de \( n \)-esferas.
Enquanto isso, os \( \sigma_n \) são os volumes das \( n \)-esferas unitárias. Em particular, \( \sigma_2 \) é a área de um disco unitário:
Isto mostra que \( \sigma_2 = \tau/2 = 3,14159\ldots \) tem mesmo um significado geométrico independente. Note, no entanto, que isso não tem nada a ver com circunferências ou diâmetros. Em outras palavras, \( \pi = C/D \) não é um membro da família \( \sigma_n \).
Então, a qual família de constantes \( \pi \) pertence naturalmente? Vamos reescrever a Eq. (1) em termos mais apropriados para generalizações a dimensões superiores:
Vemos assim que \( \pi \) é associado naturalmente a áreas de superfície divididas pela potência do diâmetro necessário para produzir uma constante adimensional. Isso sugere a introdução de uma terceira família de constantes \( \pi_n \):
Podemos expressar isto em termos da família \( \tau_n \) substituindo \( D = 2r \) na Eq. (34) e aplicando a Eq. (32):
Estamos agora finalmente em posição de entender exatamente o que há de errado com \( \pi \). O principal significado geométrico de \( 3,14159\ldots \) é que ele é a área de um disco unitário. Mas este número vem da avaliação de \( \sigma_n = \tau_n/n \) quando \( n=2 \):
É fato que isso é igual a \( \pi_2 \):
Mas esta igualdade é uma coincidência: ela ocorre apenas porque \( 2^{n-1} \) torna-se igual a \( n \) quando \( n=2 \) (isso é, \( 2^{2-1} = 2 \)). Em todas as dimensões superiores, \( n \) e \( 2^{n-1} \) são distintos. Em outras palavras, o significado geométrico de \( \pi \) é resultado de um trocadilho matemático.
6 Conclusão
Ao longo dos anos, ouvi muitos argumentos contra a incorretude de \( \pi \) e contra a corretude de \( \tau \), portanto, antes de concluir nossa discussão, permita-me responder a algumas das perguntas mais frequentes.
6.1 Perguntas frequentes
- Você está falando sério? Claro. Quero dizer, estou me divertindo com isso, e o tom é geralmente leve, mas há um propósito sério. Definir a constante do círculo como a circunferência sobre o diâmetro é uma convenção estranha e confusa. Embora adorasse ver os matemáticos mudarem seus hábitos, não estou particularmente preocupado com eles; eles podem cuidar de si mesmos. É com os neófitos que estou mais preocupado, pois eles é que sofrem as consequências: como observado na Seção 2.1, \( \pi \) é um desastre pedagógico. Tente explicar a uma criança de doze anos (ou a alguém de trinta anos) por que a medida do ângulo para um oitavo de círculo—uma fatia de pizza—é \( \pi/8 \). Espere, eu quis dizer \( \pi/4 \). Entendeu o que eu quis dizer? É loucura—pura e simples.
- Como podemos mudar de \( \pi \) para \( \tau \)? Na próxima vez que você escrever algo que usa a constante do círculo, basta dizer “por conveniência, definimos \( \tau = 2\pi \)” e prossiga como de costume. (Obviamente, isto pode levar à pergunta: “Por que você quer fazer isso?”, e admito que seria interessante poder fazer referência a uma explicação. Se ao menos alguém escrevesse, digamos, um manifesto sobre o assunto…) A maneira de levar as pessoas a começar a usar \( \tau \) é começar a usá-lo você mesmo.
- Não é tarde demais para mudar? Não seria necessário reescrever todos os livros e artigos de matemática? Não e não. É verdade que algumas convenções, embora infelizes, são efetivamente irreversíveis. Por exemplo, a escolha de Benjamin Franklin para os sinais das cargas elétricas leva o exemplo mais conhecido de corrente elétrica (elétrons livres em metais) a ser positiva quando os portadores de carga são negativos e vice-versa—e assim amaldiçoa os estudantes iniciantes de física com sinais negativos confusos desde então.25 Para alterar esta convenção iria requerer a reescrita de todos os livros (e a queima dos antigos) uma vez que é impossível dizer de relance que convenção está sendo usada. Em contrapartida, embora redefinir \( \pi \) seja efetivamente impossível, podemos trocar \( \pi \) por \( \tau \) em tempo real usando a conversão
\[ \pi \leftrightarrow \textstyle{\frac{1}{2}}\tau. \]
É meramente uma questão de substituição mecânica, completamente robusta e, de fato, totalmente reversível. A troca de \( \pi \) por \( \tau \), portanto, pode acontecer de forma incremental; diferentemente de uma redefinição, ela não precisa acontecer de uma só vez.
- Usar \( \tau \) não vai confundir as pessoas, especialmente os estudantes? Se você é inteligente o suficiente para entender a medida do ângulo radiano, é inteligente o suficiente para entender \( \tau \)—porque \( \tau \) é realmente menos confuso do que \( \pi \). Além disso, não há nada intrinsecamente confuso em dizer “Seja \( \tau = 2\pi \)”; entendido estritamente, isto é apenas uma simples substituição. Finalmente, podemos aceitar a situação como uma oportunidade de educar: a ideia de que \( \pi \) pode estar errado é interessante e os alunos podem se envolver com o material convertendo as equações em seus livros de \( \pi \) para \( \tau \) para ver por si mesmos qual é a melhor escolha.
- Isto realmente importa? Claro que isto importa. A constante do círculo é importante. As pessoas se preocupam o suficiente com isto para escrever livros inteiros sobre o assunto, para celebrá-lo em um dia específico todos os anos e para memorizar dezenas de milhares dos seus dígitos. Eu me importo o suficiente para escrever um manifesto inteiro, e você se importa o suficiente para lê-lo. É precisamente porque isto importa que é difícil admitir que a presente convenção está errada. (Quero dizer, como você contaria ao Rajveer Meena, um recordista mundial, que ele recitou 70.000 dígitos da metade da verdadeira constante do círculo?) Como a constante do círculo é importante, é importante defini-la direito, e vimos neste manifesto que o número certo é \( \tau \). Embora \( pi \) seja de grande importância histórica, o significado matemático de \( \pi \) é que ele é metade de \( \tau \).
- Por que \( \pi \) foi usado primeiro? Como notação, \( \pi \) foi popularizado há cerca de 300 anos por Leonhard Euler (baseado no trabalho de William Jones), mas as origens de \( \pi \)-o-número se perdem nas brumas do tempo. Eu suspeito que a convenção de usar \( C/D \) ao invés de \( C/r \) surgiu simplesmente porque é mais fácil medir o diâmetro de um objeto circular do que medir seu raio. Mas isso não o torna boa matemática, e fico surpreso que Arquimedes, que famosamente aproximou a constante do círculo, não percebeu que \( C/r \) era o número mais fundamental. Fico ainda mais surpreso que Euler não tenha corrigido o problema quando teve a oportunidade; ao contrário de Arquimedes, Euler tinha o benefício da notação algébrica moderna, que (como vimos começando na Seção 2.1) torna as relações subjacentes entre os círculos e a constante do círculo absolutamente claras. Pode parecer incrível, mas Euler realmente usou o símbolo \( \pi \) para significar tanto \( C/D \) quanto \( C/r \) em momentos diferentes! Que pena que ele não padronizou a escolha mais conveniente.
- Por que este assunto lhe interessa? Primeiro, como um buscador da verdade, eu me preocupo com a corretude da explicação. Segundo, como professor, eu me preocupo com a clareza da exposição. Terceiro, como hacker, adoro um bom hack. Quarto, como estudante de história e da natureza humana, acho fascinante que o absurdo de \( \pi \) tenha estado à vista por séculos antes que alguém parecesse notar. Além disso, muitas das pessoas que não perceberam a verdadeira constante do círculo estão entre as pessoas mais racionais e inteligentes que já viveram. O que mais podemos estar deixando passar despercebido, a espera que o descubramos?
- Você é, tipo, louco? Isso não é da sua conta, mas não. Apesar de eu ocasionalmente usar sapatos incomuns, sou normal em todos os aspectos a todas as aparências externas. Você nunca imaginaria que, longe de ser um cidadão comum, eu sou de fato um notório propagandista matemático.
- Mas e como ficam as piadas? Chegamos agora à objeção final. Eu sei eu sei, “\( \pi \) in the sky” é muito inteligente.26 Mas, \( \tau \) também é cheio de possibilidades. O \( \tau \)ismo nos diz que: não é \( \tau \) que é um pedaço de \( \pi \), mas \( \pi \) que é um pedaço de \( \tau \)– meio \( \tau \), para ser exato. A identidade \( e^{i\tau} = 1 \) diz: “Seja um com o \( \tau \)”. E embora a observação de que “uma rotação de uma volta é 1” possa parecer uma \( \tau \)-tologia, ela é a verdadeira natureza do \( \tau \). Ao contemplarmos essa natureza em busca do caminho do \( \tau \), devemos lembrar que o \( \tau \)ismo é baseado na razão, não na fé: os \( \tau \)istas nunca são \( \pi \)os.
6.2 Aceite o tau
Vimos em O Manifesto Tau que a escolha natural para a constante do círculo é a razão entre a circunferência de um círculo e, não o seu diâmetro, mas o seu raio. Este número precisa de um nome e espero que você se junte a mim ao chamá-lo de \( \tau \):
O uso é natural, a motivação é clara e as implicações são profundas. Além disso, ele vem com um diagrama muito bacana (Figura 17). Vemos na Figura 17 um movimento através do yang (“claro, branco, subindo”) até \( \tau/2 \) e um retorno através do yin (“escuro, preto, descendo”) de volta ao \( \tau \).27 Usar \( \pi \) ao invés de \( \tau \) é como ter yang sem yin.
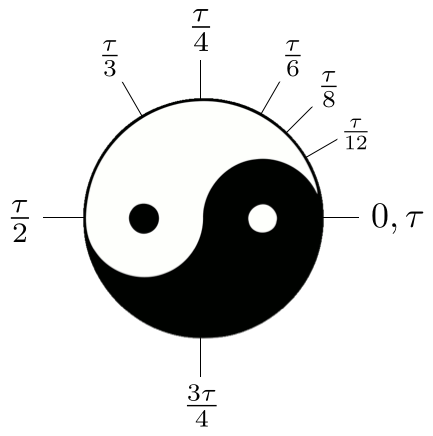
6.3 O Dia do Tau
O Manifesto Tau foi lançado pela primeira vez no Dia do Tau: 28 de junho (6/28, em notação estadunidense) de 2010. O Dia do Tau é um momento para celebrar e se regozijar em todas as coisas matemáticas.28 Se você quiser receber atualizações sobre \( \tau \), incluindo notificações sobre possíveis eventos futuros do Dia do Tau, entre na lista de discussão de O Manifesto Tau abaixo. E se você acha que os assados circulares do Dia do Pi parecem saborosos, você não perde por esperar—o Dia do Tau tem o dobro de pi(e)29!
Share the τ Manifesto
Agradecimentos
Em primeiro lugar, gostaria de agradecer a Bob Palais por escrever “\( \pi \) Está Errado!”. Não me lembro de quão profundas já eram minhas suspeitas sobre \( \pi \) antes de encontrar esse artigo, mas “\( \pi \) Está Errado!” definitivamente abriu os meus olhos, e cada seção de O Manifesto Tau tem com ele uma dívida de gratidão. Também gostaria de agradecer a Bob pelos seus comentários úteis sobre este manifesto e, principalmente, por tê-lo recebido com tanta esportividade.
Tenho pensado em O Manifesto Tau há algum tempo e muitas das idéias apresentadas aqui foram desenvolvidas em conversas com meu amigo Sumit Daftuar. Sumit foi um ótimo ouvinte e, ocasionalmente, advogado do diabo, e sua visão como professor e como matemático influenciou meu pensamento enormemente.
Também recebi incentivo e comentários úteis de vários leitores. Gostaria de agradecer a Vi Hart e Michael Blake pelos seus incríveis vídeos inspirados em \( \tau \), assim como a Don “Blue” McConnell e Skona Brittain por ajudarem a tornar \( \tau \) parte da cultura nerd (através do aplicativo time-in-\( \tau \) para iPhone e do tau clock, respectivamente). A linda interpretação do símbolo yin-yang usado em O Manifesto Tau deve-se a uma sugestão de Peter Harremoës, que (como observado acima) tem a rara distinção de ter proposto o uso de \( \tau \) para a constante do círculo independentemente. Outro \( \tau \)ista pre–O Manifesto Tau, Joseph Lindenberg, também tem sido um forte defensor, e seu entusiasmo é muito apreciado. Recebi várias boas sugestões de Christopher Olah, particularmente em relação à interpretação geométrica da identidade de Euler, e a Seção 2.3.2 sobre as identidades eulerianas foi inspirada por uma excelente sugestão de Timothy “Patashu” Stiles. Don Blaheta antecipou e inspirou parte do material sobre as hiperesferas, e John Kodegadulo juntou tudo de um modo particularmente claro e divertido. Foi então que Jeff Cornell, com sua observação sobre a importância de \( \tau/4 \) nesse contexto, abalou minha fé e explodiu minha cabeça.
Por fim, gostaria de agradecer a Wyatt Greene pela sua revisão extraordinariamente detalhista de um rascunho de pré-lançamento do manifesto; entre outras coisas, se um dia você precisar de alguém para lhe dizer que “praticamente toda a [agora excluída] seção 5 está uma porcaria”, Wyatt é o cara.
Direito autoral
O Manifesto Tau. Direitos reservados por Michael Hartl © 2010–2018.

