Манифест тау
Майкл Хартл (Michael Hartl)
перевод: Александр Алексеевич Адамов (translation by Aleksandr Alekseevich Adamov)
День числа тау 2010
обновлён в День числа тау 2020
1 Константа окружности
Манифест тау посвящён одному из самых важных, а возможно, самому важному числу в математике: константе окружности, связывающей длину окружности с её линейным измерением. Тысячи лет окружность считалась самой идеальной геометрической фигурой, и в константе окружности содержится вся геометрия окружности в едином числе. Конечно, традиционный выбор для константы окружности — это \( \pi \) (пи), но, как математик Боб Палэй замечает в своей восхитительной статье "\( \pi \) Is Wrong!",1 \( \pi \) неправильное число. Наступило время всё исправить.
1.1 Нескромное предложение
Мы начнём исправлять ущерб, нанесённый \( \pi \), для начала поняв само пресловутое число. Традиционное определение константы окружности делает \( \pi \) равным отношению длины окружности к её диаметру (ширине):2
У этого числа \( \pi \) есть много замечательных свойств — например, оно иррационально и, конечно, трансцендентно — и оно присутствует в огромном количестве математических формул.
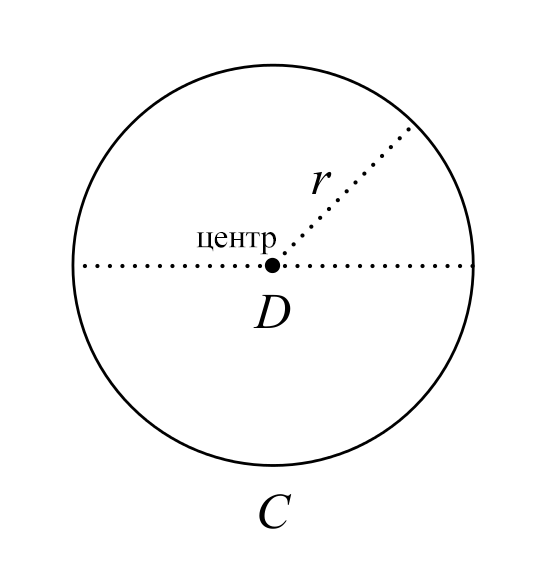
Должно быть очевидным, что \( \pi \) не "неправильно" в том смысле, что его значение неточное; значение числа \( \pi \) точное, и у него есть все свойства, которые ему приписывают математики. Когда мы говорим, что "\( \pi \) — неправильное число", имеется ввиду то, что \( \pi \) — запутанный и неестественный выбор для константы окружности. В частности, окружность определяется как множество точек, удалённых на одно и то же расстояние, радиус, от заданной точки, центра окружности (Картинка 1). В то время, как существует бесконечное количество геометрических фигур с постоянной шириной, (Картинка 2),3 существует только одна фигура с постоянным радиусом. Это намекает на то, что более естественное определение для константы окружности должно использовать \( r \) вместо \( D \):
Так как диаметр окружности вдвое больше радиуса, эта величина численно равна \( 2\pi \). Как и \( \pi \), это число трансцендентно и, следовательно, иррационально, и (как мы увидим в Разделе 2) появляется в математических формулах с такой же частотой.
В статье "\( \pi \) Is Wrong!" Боб Палэй приводит веские доводы в пользу второго из этих двух определений для константы окружности и, по моему мнению, заслуживает статус первого человека, который указал на это большой аудитории. Он называет истинную константу окружности "один оборот" и также создаёт новый символ для этого числа (Картинка 3). Как мы позже увидим, определение этого числа верно, но, к сожалению, символ довольно странен, и (как обсуждается в Разделе 4), скорее всего, не будет широко использоваться.

Манифест тау посвящён утверждению, что правильный ответ на "\( \pi \) неправильное число" — это: "да, на самом деле". И истинная константа окружности заслуживает соответствующее имя. Как можно было уже догадаться, Манифест тау предлагает, чтобы этим именем была греческая буква \( \tau \) (тау):
В рамках этого Манифеста мы убедимся, что число \( \tau \) — это правильный выбор, и покажем с помощью конкретных примеров использования (Раздел 2 и Раздел 3) и приведением прямых доводов (Раздел 4), что буква \( \tau \) также является естественным выбором.
1.2 Сильный враг
Перед тем, как мы приступим к демонстрации того, что \( \tau \) — это единственный естественный выбор для константы окружности, давайте признаем, против чего мы боремся, так как сотни лет существует мощная теория заговора, направленная на распространение про-\( \pi \) пропаганды. Целые книги написаны про заслуги \( \pi \). (Только подумайте, книги!) И иррациональная любовь к \( \pi \) распространилась до самых высот; например, на "День числа пи 2010" Google изменил свой логотип, чтобы оказать честь \( \pi \) (Картинка 4).
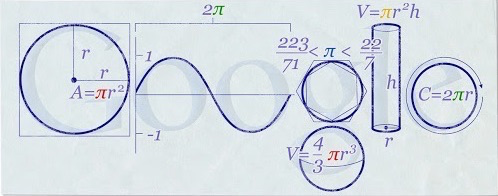
В то же время, некоторые люди запоминают дюжины, сотни, даже тысячи цифр этого мистического числа. Какой несчастный человек запоминает даже 40 цифр \( \pi \) (Картинка 5)?4

Воистину, сторонники \( \tau \) стоят перед сильным оппонентом. И всё же, на нашей стороне стоит мощная вещь — истина.
2 Число тау
Мы увидели в Разделе 1.1, что число \( \tau \) может также быть записано как \( 2\pi \). Как замечено в статье “\( \pi \) Is Wrong!”, очень интересно понаблюдать за тем, с какой удивительной частотой комбинация \( 2\pi \) появляется в математике. Возьмём, к примеру, интегралы по всему пространству в полярных координатах:
Интегрирование по \( \theta \) всегда происходит до \( 2\pi \). Та же самая величина появляется в определении гауссовского (нормального) распределения,
и снова — в преобразовании Фурье,
Также присутствует в интегральной формуле Коши,
и в корне n-й степени,
и в значениях дзета-функции Римана для положительных чётных чисел:5
Эти формулы не были выбраны специально — откройте свой любимый учебник по математике или физике и убедитесь сами. Таких примеров ещё очень много, и вывод ясен: в величине \( 2\pi \) есть что-то особенное.
Чтобы хорошенько разобраться в этой загадке, мы должны вернуться к первым принципам и посмотреть на природу окружностей, и особенно природу углов. Хотя этот материал, скорее всего, уже известен читателю, будет неплохо повторить его ещё раз, так как в нём лежит понимание \( \tau \).
2.1 Окружности и углы
Существует тесная связь между окружностями и углами, как показано в Картинке 6. Так как у концентрических окружностей в Картинке 6 разные радиусы, лучи в фигуре отрезают дуги разной длины, но угол \( \theta \) (тета) тот же самый в каждом случае. Другими словами, размер угла не зависит от радиуса окружности, используемой для того, чтобы определить дугу. Главная задача измерения угла — это создать систему, в которой будет эта радиус-инвариантность.

Возможно, самая простая система углов — это градусы, где окружность делится на 360 равных частей. Ученикам, изучающим тригонометрию, говорят запоминать особые углы, показанные на Картинке 7.

Более фундаментальная система измерения углов заключается в прямом сравнении длины дуги \( s \) с радиусом \( r \). Хоть и длины дуг в Картинке 6 разнятся, их длина растёт пропорционально радиусу, поэтому отношение длины дуги к радиусу в каждом случае то же самое:
Это даёт следующее определение величины угла в радианах:
У этого определения есть требуемое свойство радиус-инвариантности, и так как и \( s \) , и \( r \) измеряются в одних и тех же единицах измерения, радианы безразмерны по определению. Использование радиан ведёт к кратким и элегантным формулам в математике; к примеру, формула для производной \( \sin\theta \) истинна только в том случае, когда \( \theta \) выражен в радианах:
Естественно, особые углы в Картинке 7 могут быть выражены в радианах, и когда вы учились в школе и изучали тригонометрию, то, скорее всего, запоминали значения в Картинке 8. (Я называю эту систему измерения \( \pi \)-радианы, чтобы подчеркнуть тот факт, что они записаны, используя \( \pi \).)


Достаточно немного об этом подумать, и становится ясно, что, так называемые, "особые" углы на самом деле простые рациональные доли полной окружности, как показано в Картинке 9. Это наводит на то, чтобы посмотреть на Ур. (4) ещё раз и переписать длину дуги \( s \) как долю \( f \) от всей длины окружности\( C \), т.е.\( s = f C \):
Заметьте, как естественно \( \tau \) появляется в этом анализе. Если вы верующий в \( \pi \), я боюсь, что получившаяся диаграмма особых углов (Картинка 10) сотрясёт вашу веру до самого основания.

Хотя и есть много других доводов в пользу \( \tau \), Картинка 10 может показаться самой убедительной. Мы также можем увидеть гений Боба Палэя в Картинке 10, где он сопоставляет константу окружности с “одним оборотом”: \( \tau \) — это измерение углов в радианах для одного оборота вокруг окружности. Более того, следует заметить, что с \( \tau \) нечего запоминать наизусть: двенадцатая оборота — это \( \tau/12 \), восьмая оборота — это \( \tau/8 \), и так далее. Использование \( \tau \) убивает двух зайцев одним выстрелом: оно объединяет концептуальную ясность со всеми конкретными плюсами радиан; абстрактное значение, скажем, \( \tau/12 \) очевидно, но оно в то же самое время является обычным числом:
Сравнив Картинку 8 с Картинкой 10, мы видим откуда эти надоедливые \( 2\pi \): один оборот — это \( 1\tau \), но в то же время \( 2\pi \). Численно они равны, но концептуально довольно разные.
Отступление
Ненужные двойки, появляющиеся из-за использования \( \pi \), достаточно раздражают сами по себе, но намного более серьёзна их тенденция сокращаться с любым чётным числом. Абсурдные результаты, такие как половина \( \pi \) для четверти оборота, скрывают связь между измерением угла и константой окружности. Те, кто считают что "не важно", какую константу окружности использовать, я просто прошу посмотреть на Картинку 8, Картинку 9, и Картинку 10 глазами ребёнка. Вы сразу увидите, что с точки зрения новичка в математике, использовать \( \pi \) вместо \( \tau \) — это педагогическая катастрофа.
2.2 Функции окружности
Хотя измерение углов в радианах представляет один из самых веских доводов в пользу истинной константы окружности, стоит также проверить плюсы \( \pi \) и \( \tau \) в других контекстах. Мы начнём с рассмотрения важных элементарных функций \( \sin\theta \) и \( \cos\theta \). Они известны как "функции окружности", потому что им соответствуют точки на единичной окружности (т.е. окружности с радиусом \( 1 \)), синус и косинус являются фундаментальными функциями тригонометрии (Картинка 11).

Давайте изучим графики функций окружности, чтобы лучше понять их поведение.6 Вы можете заметить из Картинки 12 и Картинки 13, что обе функции периодические с периодом \( T \). Как показано на Картинке 12, функция синуса \( \sin\theta \) начинается с нуля, достигает максимума на четверти периода, проходит через ноль на половине периода, достигает минимума на трёх четвертях периода и возвращается на ноль после одного полного периода. В то же время, функция косинуса \( \cos\theta \) начинается на максимуме, достигает минимума на половине периода и проходит через ноль в одной четверти и трёх четвертях периода (Картинка 13). На обеих картинках показано значение \( \theta \) (в радианах) в каждой особой точке.


Конечно, так как и синус, и косинус проходят через один полный цикл во время одного оборота, то \( T = \tau \); т.е. у функций окружности периоды равны константе окружности. Как следствие, "особые" значения \( \theta \) крайне естественны: четверть периода — это \( \tau/4 \), пол периода — это \( \tau/2 \) и т.д. На самом деле, когда я создавал Картинку 12, то на секунду задумался о том, чему численно равно значение \( \theta \) для нуля функции синуса. Так как ноль появляется через пол периода, и так как \( \tau \approx 6,28 \), быстрое вычисление в уме приводит к следующему результату:
Именно. Я был удивлён тому, что уже забыл, что \( \tau/2 \) иногда называется “\( \pi \)”. Возможно, то же самое случилось с вами сейчас. Добро пожаловать в мой мир.
2.3 Тождество Эйлера
Меня нельзя было бы простить, если в этом Манифесте не было бы написано про тождество Эйлера, иногда называемое “самым красивым уравнением в математике”. Это тождество связано с комплексным возведением в степень, которое в свою очередь глубоко связано как и с функциями окружности, так и с самой геометрией окружности.
В зависимости от того, какой путь выбран, следующее уравнение может быть или доказано, или взято как определение; в любом случае, оно довольно замечательное:
Известное как формула Эйлера (в честь Леонарда Эйлера), это уравнение связывает экспоненту с воображаемым аргументом с синусом и косинусом, функциями окружности, а также с мнимой единицей \( i \). Хотя доказательство формулы Эйлера вне рамок этого Манифеста, её истинность и важность неоспоримы.
Определение значения Ур. (5) при \( \theta = \tau \) приводит к тождеству Эйлера:7
Ур. (6), выраженное в словах, делает следующее фундаментальное наблюдение:
Комплексная экспонента, возведённая в степень константы окружности, равна единице.
Геометрически, умножение на \( e^{i\theta} \) соответствует повороту комплексного числа на угол \( \theta \) в комплексной плоскости, что наводит на вторую интерпретацию тождества Эйлера:
Поворот на один оборот — это 1.
Так как число \( 1 \) — это мультипликативная единица, геометрическое значение \( e^{i\tau} = 1 \) — поворот точки в комплексной плоскости на один оборот, возвращает её в изначальное положение.
Как и в случае с радианами, мы видим естественную параллель между \( \tau \) и одним оборотом вокруг окружности. Безусловно, приравнивание \( \tau \) к "одному обороту" делает тождество Эйлера почти тавтологией.8
Не самое красивое уравнение
Конечно, традиционная форма тождества Эйлера записывается с помощью \( \pi \) вместо \( \tau \). Чтобы вывести её, мы начнём с определения значения формулы Эйлера в точке \( \theta = \pi \), и это даёт
Но этот знак минуса настолько уродлив, что Ур. (7) почти всегда сразу преобразовывают в следующее "красивое" уравнение:
На этом этапе показывающий это уравнение обычно делает какое-то грандиозное утверждение о том, как Ур. (8) связывает \( 0 \), \( 1 \), \( e \), \( i \), и \( \pi \), а затем называет их "пятью самыми важными числами в математике”.
В этом контексте удивительно то, сколько людей жалуются, что Ур. (6) связывает между собой только четыре из этих пяти чисел. Ладно:
Ур. (9), без преобразования, на самом деле связывает между собой пять самых важных чисел в математике: \( 0 \), \( 1 \), \( e \), \( i \), и \( \tau \).
Тождества Эйлера
Так как в уравнении можно прибавить ноль в любом месте, прибавление \( 0 \) в Ур. (9) довольно несерьёзный аргумент против \( e^{i\pi} + 1 = 0 \), но тождество \( e^{i\pi} = -1 \) говорит о нечто более серьёзном. Давайте посмотрим, что случится, если мы перепишем его с помощью \( \tau \):
Геометрически, это уравнение говорит, что поворот на половину оборота — это то же самое, что и умножение на \( -1 \). И это на самом деле так: после поворота на \( \tau/2 \) радиан комплексное число \( z = a + ib \) превращается в \( -a - ib \), что, конечно же, просто \( -1\cdot z \).
Написав "изначальную" форму тождества Эйлера с помощью \( \tau \), мы видим в Ур. (7) прозрачный геометрический смысл, который отсутствует, если записать тождество с помощью \( \pi \). (Конечно, \( e^{i\pi} = -1 \) можно интерпретировать как поворот на \( \pi \) радиан, но почти всегда происходящее преобразование \( e^{i\pi} + 1 = 0 \) показывает, как использование \( \pi \) отвлекает от естественного геометрического смысла тождества.) У тождества, соответствующего четверти оборота, есть похожая геометрическая интерпретация: определение значения Ур. (5) в точке \( \tau/4 \) даёт \( e^{i\tau/4} = i \), показывающее, что поворот на четверть в комплексной плоскости — это то же самое, что и умножение на \( i \); таким же образом, \( e^{i\cdot(3\tau/4)} = -i \) говорит что поворот на три четверти — это то же самое, что и умножение на \( -i \). Все эти результаты, которые мы назовём тождествами Эйлера, находятся в Таблице 1.
| Угол поворота | Тождество Эйлера | ||
| \( 0 \) | \( e^{i\cdot0} \) | \( = \) | \( 1 \) |
| \( \tau/4 \) | \( e^{i\tau/4} \) | \( = \) | \( i \) |
| \( \tau/2 \) | \( e^{i\tau/2} \) | \( = \) | \( -1 \) |
| \( 3\tau/4 \) | \( e^{i\cdot(3\tau/4)} \) | \( = \) | \( -i \) |
| \( \tau \) | \( e^{i\tau} \) | \( = \) | \( 1 \) |
Можно продолжить этот анализ дальше, заметив, что для любого угла \( \theta \) значение \( e^{i\theta} \) может быть интерпретировано как точка, лежащая на единичной окружности в комплексной плоскости. Так как комплексная плоскость приравнивает горизонтальную ось с вещественной частью числа и вертикальную ось с мнимой частью, формула Эйлера говорит нам, что \( e^{i\theta} \) соответствует координатам \( (\cos\theta, \sin\theta) \). Подставляя значения "особых" углов из Картинки 10 в Ур. (5) даёт точки, показанные в Таблице 2, и построив график по этим точкам в комплексной плоскости, получаем Картинку 14. Сравнение Картинки 14 с Картинкой 10 быстро развеивает любые сомнения о том, выбор какой константы окружности лучше показывает отношение между формулой Эйлера и геометрией окружности.
| Полярная форма | Прямоугольная форма | Координаты |
| \( e^{i\theta} \) | \( \cos\theta + i\sin\theta \) | \( (\cos\theta, \sin\theta) \) |
| \( e^{i\cdot0} \) | \( 1 \) | \( (1, 0) \) |
| \( e^{i\tau/12} \) | \( \frac{\sqrt{3}}{2} + \frac{1}{2}i \) | \( (\frac{\sqrt{3}}{2}, \frac{1}{2}) \) |
| \( e^{i\tau/8} \) | \( \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i \) | \( (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) \) |
| \( e^{i\tau/6} \) | \( \frac{1}{2} +\frac{\sqrt{3}}{2} i \) | \( (\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( e^{i\tau/4} \) | \( i \) | \( (0, 1) \) |
| \( e^{i\tau/3} \) | \( -\frac{1}{2} +\frac{\sqrt{3}}{2} i \) | \( (-\frac{1}{2}, \frac{\sqrt{3}}{2}) \) |
| \( e^{i\tau/2} \) | \( -1 \) | \( (-1, 0) \) |
| \( e^{i\cdot(3\tau/4)} \) | \( -i \) | \( (0, -1) \) |
| \( e^{i\tau} \) | \( 1 \) | \( (1, 0) \) |

3 Площадь окружности: смертельный удар
Если вы пришли сюда как верующий в \( \pi \), то сейчас уже должны поставить свою веру под сомнение. \( \tau \) — такое естественное число, его смысл такой прозрачный — не существует ли примера, где во всей своей красе сияет \( \pi \)? Что-то припоминается — да, такая формула существует — это формула для площади окружности! Узрите:
Нет, погодите. Формула площади окружности всегда записывается, используя радиус, вот так:
Здесь мы видим \( \pi \) без каких-либо чисел впереди него, в одном из самых важных уравнений в математике — формуле, впервые доказанной самим Архимедом. Порядок восстановлен! И всё же, название этого раздела звучит зловеще... Если это уравнение показывает победу \( \pi \), как оно может также являться смертельным ударом по нему самому?
3.1 Квадратичные формы
Давайте изучим этот образец совершенства числа \( \pi \), \( A = \pi r^2 \). Сначала заметим, что в нём фигурирует диаметр — нет, погодите, радиус — возведённый во вторую степень, что делает формулу простой квадратичной формой. Такие формы появляются во многих контекстах; как физик, мои любимые примеры — из базовой программы физики. Сейчас мы по очереди взглянем на несколько таких примеров.
Падение в однородном гравитационном поле
Галилео Галилей обнаружил, что скорость тела, падающего в однородном гравитационном поле, пропорциональна времени падения:
Константа пропорциональности — ускорение свободного падения \( g \):
Так как скорость — это производная положения, мы можем рассчитать расстояние, которое прошло тело в падении с помощью интегрирования:
Потенциальная энергия в пружине
Роберт Гук обнаружил, что внешняя сила, необходимая для того, чтобы растянуть пружину, пропорциональна расстоянию, на которое пружина была растянута:
Константа пропорциональности — коэффициент упругости \( k \):9
Потенциальная энергия в пружине тогда равна работе, совершённой внешней силой:
Энергия движения
Исаак Ньютон обнаружил, что сила, приложенная к телу, пропорциональна его ускорению:
Константа пропорциональности — масса \( m \):
Энергия движения, или кинетическая энергия, равна механической работе, совершённой при ускорении массы до скорости \( v \):
3.2 Предчувствие дурного
Увидев несколько примеров квадратичных форм в физике, у вас должно появиться дурное предчувствие при нашем возвращении к геометрии окружности. Это ощущение оправдано.

Как можно увидеть в Картинке 15, площадь окружности может быть рассчитана разбиванием её на кольца длиной \( C \) и шириной \( dr \), где площадь каждого кольца равна \( C\,dr \)
Длина окружности пропорциональна её радиусу:
Константа пропорциональности — это \( \tau \):
Тогда площадь окружности — это интеграл по всем кольцам:
Если вы ещё были на стороне \( \pi \) в начале этого раздела, ваш мозг уже взорвался. Так как даже в этом случае, где \( \pi \) должен сиять, есть отсутствующий множитель \( 2 \). Конечно, изначальное доказательство Архимеда показывает, что площадь окружности не \( \pi r^2 \), а то, что она равна площади прямоугольного треугольника с основанием \( C \) и высотой \( r \). Применяя формулу для площади треугольника, мы получаем:
Этот множитель, равный одной второй, невозможно оставить позади (Таблица 3).
| Величина | Символ | Формула |
| Расстояние, на которое упало тело | \( y \) | \( \textstyle{\frac{1}{2}}gt^2 \) |
| Энергия пружины | \( U \) | \( \textstyle{\frac{1}{2}}kx^2 \) |
| Кинетическая энергия | \( K \) | \( \textstyle{\frac{1}{2}}mv^2 \) |
| Площадь окружности | \( A \) | \( \textstyle{\frac{1}{2}}\tau\,r^2 \) |
Quod erat demonstrandum
В этом Манифесте мы собирались показать, что \( \tau \) — истинная константа окружности. Так как формула для площади окружности, можно сказать, была последним лучшим доводом в пользу \( \pi \), я наберусь смелости и скажу: Q.E.D.
4 Конфликт и сопротивление
Несмотря на неоспоримую демонстрацию превосходства \( \tau \), всё равно есть те, кто противятся идее, как с точки зрения записи, так и с точки зрения концепции числа. В этом разделе мы поговорим о том, что беспокоит тех, кто принимает число, но не символ. Затем приведём контраргументы вопреки многим доводам против самого \( C/r \), включая, так называемый, “Pi Manifesto” ("Манифест пи"), который защищает первенство \( \pi \). В этом контексте мы обсудим довольно сложную тему — объём гиперсферы (Раздел 5.1), что поменяет и усилит доводы в Разделе 3 про площадь окружности.
4.1 Один оборот
Настоящее испытание любой системы обозначений — это использование; увидев, как \( \tau \) используется в этом Манифесте, вы, возможно, уже убедились, что этот символ хорошо выполняет своё предназначение. Но для такой фундаментальной константы, как \( \tau \), было бы хорошо иметь более глубокие причины для выбора этого символа. Почему не \( \alpha \), к примеру, или \( \omega \)? Что такого хорошего в \( \tau \)?
Есть две главные причины использовать \( \tau \) для константы окружности. Первая заключается в том, что \( \tau \) внешне напоминает \( \pi \): после столетий использования ассоциация \( \pi \) с константой окружности неизбежна, и использование \( \tau \) получает пользу от этой ассоциации, вместо борьбы с ней. (Конечно, горизонтальная линия в каждой букве намекает на ассоциацию "ног" со знаменателями, так что у \( \pi \) две ноги в знаменателе, в то время как у \( \tau \) только одна. С этой точки зрения, отношение \( \tau = 2\pi \) абсолютно естественно.)10
Вторая причина заключается в том, что \( \tau \) соответствует одному обороту (англ. turn), и, как вы могли уже заметить, “\( \tau \)” и “turn” оба начинаются со звука "т". В этом лежала изначальная мотивация в выборе буквы \( \tau \), и это не совпадение: английское слово “turn” происходит от греческого слова τόρνος (торнос), что означает "токарный станок". Использование математического шрифта для первой буквы в слове τόρνος даёт нам \( \tau \).
После изначального запуска Манифеста тау я узнал, что Питер Хэрримоэс независимо предложил использовать \( \tau \) автору статьи “\( \pi \) Is Wrong!” Бобу Палэю в 2010, Джон Фишер предложил \( \tau \) в посте на Usenet в 2004, а Джозеф Линдерберг предвидел как довод, так и символ более чем за 20 лет до этого!11 Доктор Хэрримоэс, в частности, акцентировал внимание на доводе, сделанном в Разделе 1.1: использование \( \tau \) даёт константе окружности имя. Так как \( \tau \) — обыкновенная буква греческого алфавита, люди, встречающие её в первый раз, сразу смогут её произнести.
Двусмысленная система обозначений
Конечно, с любым новым символом появляется возможность путаницы с существующей системой обозначений. Как было замечено в Разделе 1.1, в статье “\( \pi \) Is Wrong!” эта проблема избегается созданием нового символа (Картинка 3). Такое уже случалось; например, в ранние дни квантовой механики Макс Планк ввёл новую константу \( h \), которая связывает энергию частицы света с её частотой (через уравнение \( E = h\nu \)), но позже физики осознали, что намного удобнее использовать \( \hbar \), где \( \hbar \) — это просто \( h \), поделённое на… эмм… \( 2\pi \) — и этот символ теперь везде используется.
Но сделать так, чтобы новый символ приняли, трудно: ему нужно дать название, которое должно стать широко известным, и сам символ должен быть добавлен во все системы, необходимые для его отображения и печати. Более того, пропагандирование нового символа для \( 2\pi \) потребовало бы кооперации с академическим математическим сообществом, которое до сих пор было апатично (в лучшем случае) или враждебно (в худшем) на тему \( \pi \) против \( \tau \). Использование существующего символа позволяет обойти стороной математический истеблишмент.12
Вместо создания нового символа, в Манифесте тау предлагается использование уже существующей греческой буквы. Как следствие, так как \( \tau \) уже используется в некоторых существующих контекстах, мы должны поговорить о потенциальном конфликте с существующей практикой. К счастью, наш символ используется довольно редко. Более того, в то время как \( \tau \) используется для некоторых конкретных переменных — например, напряжения сдвига в машиностроении, момента силы в механике и собственного времени в особой и общей теориях относительности — не существует всеобщего противоречащего использования.13 В этих случаях мы можем игнорировать двусмысленность или обойти проблему стороной, выборочно поменяв уже используемые символы. Например, можно использовать \( N \) для момента силы14 или \( \tau_p \) для собственного времени.
Несмотря на эти доводы, потенциальные конфликты в использовании символов оказались самым большим источником сопротивления \( \tau \). Некоторые люди, с которыми я разговаривал, напрочь исключают, что \( \tau \) (или, по-видимому, любой другой уже использующийся символ) сможет обойти эти проблемы. Но у учёных и инженеров высокая терпимость к двусмысленности в системах обозначений, и утверждение, что \( \tau \)-константа-окружности не может сосуществовать с другими использованиями данного символа, закрывает глаза на значительные доказательства обратного.
Один пример легко переносимой двусмысленности происходит в квантовой механике, где мы встречаем следующую формулу для радиуса Бора, которая (грубо говоря) является "размером" атома водорода в его самом низком энергетическом уровне (основном уровне):
где \( m \) — это масса электрона, и \( e \) — его заряд. В то же самое время, основной уровень описывается величиной, известной как волновая функция, которая падает экспоненциально с радиусом на масштабах длины, заданных радиусом Бора:
где \( N \) — это нормирующая постоянная.
Уже заметили проблему? Скорее всего, нет — в этом и суть. "Проблема" заключается в том, что \( e \) в радиусе Бора и \( e \) в волновой функции — не одна и та же \( e \): первая — это заряд электрона, в то время как вторая — это основание натурального логарифма. Более того, если мы подставим под \( a_0 \) его значение в Ур. (10), то получим
в котором есть \( e \), возведённое в степень чего-то содержащего в себе ещё одну \( e \). Дела ещё хуже, чем кажутся, потому что \( N \) содержит в себе ещё одну \( e \):
Я не сомневаюсь в том, что если бы символ \( e \) использовался] для основания натурального логарифма, то на любое предложение использовать эту букву для основания натурального логарифма отвечали бы, что это не получится, так как это противоречит другим использованиям этого символа. И всё же, на практике ни у кого никогда не было никаких проблем с использованием \( e \) в обоих описанных выше контекстах. Существует много других примеров, включая ситуации, где даже \( \pi \) используется для двух разных вещей.15 Трудно себе представить, как использование \( \tau \) для нескольких разных вещей является исключением из правил.
Кстати, \( \pi \)-педанты (и таковых, как я понял, очень много) могли заметить, что волновая функция основного уровня водорода содержит в себе множитель \( \pi \):
С первого взгляда, похоже, что это более естественно, чем версия с \( \tau \):
Как всегда, внешность обманчива: значение \( N \) задаётся произведением
, которое показывает, что константа окружности "входит" в вычисление через \( 1/\sqrt{2\pi} \), т.е. \( 1/\sqrt{\tau} \). Как и в случае с площадью окружности, сокращение с последующим "голым" \( \pi \) — это всего лишь совпадение.
4.2 Манифест пи
Хотя и большинство аргументов против \( \tau \) приходят через случайную переписку по электронной почте и различными комментариями в интернете, есть и организованная оппозиция. В частности, с начала публикации Манифеста тау в июне 2010, появился “Pi Manifesto” ("Манифест пи"), чтобы привести доводы в пользу традиционной константы окружности. Этот раздел, и два раздела после него, содержат опровержения этих аргументов. Невозможно избежать того, что контраргументы будут немногословны и технически более сложные, чем остальная часть этого Манифеста, но даже если не сильно вдаваться в подробности того, что будет написано далее, у вас всё равно останется впечатление слабости Манифеста пи.
В то время, как мы можем определённо считать появление Манифеста пи хорошим признаком продолжающегося интереса к этой теме, Манифест делает несколько ложных утверждений. Например, в нём говорится, что множитель \( 2\pi \) в гауссовском (нормальном) распределении — это совпадение, и то, что оно может быть записано более естественно как
Это не так: множитель \( 2\pi \) приходит в формулу через возведение в квадрат ненормированного гауссовского распределения и переключение в полярную систему координат, что ведёт к множителю \( 1 \) от радиального интеграла и \( 2\pi \) — от углового интеграла. Как и в случае с площадью окружности, множитель \( \pi \) появляется из-за \( 1/2\times 2\pi \), а не просто от \( \pi \).
Также в тексте есть связанное утверждение, что Гамма-функция в точке \( 1/2 \) записывается в более естественной форме с помощью \( \pi \):
где
Но \( \Gamma(\frac{1}{2}) \) можно свести к такому же гауссовскому интегралу, как и в нормальном распределении (задав \( u = x^{1/2} \)), так что \( \pi \) в этом случае на самом деле тоже является \( 1/2\times 2\pi \). Конечно, во многих аргументах, приведённых в Манифесте пи, константа окружности появляется через интеграл по всем углам, т.е. по всем \( \theta \) от \( 0 \) до \( \tau \).
Манифест пи также изучает некоторые формулы для правильных многоугольников с количеством сторон \( n \) (или “\( n \)-угольников”). К примеру, в Манифесте замечено, что сумма всех внутренних углов \( n \)-угольника задаётся формулой
Контраргумент был приведён в статье “Pi Is Wrong!”, в которой замечается следующее (перевод с англ.): “Сумма всех внутренних углов (треугольника) равна \( \pi \), согласен. Но сумма всех внешних углов любого многоугольника, из которой легко вывести сумму всех внутренних углов и которую можно обобщить до интеграла кривизны простой замкнутой кривой, равна \( 2\pi \).” В дополнение, в Манифесте пи предложена формула для площади \( n \)-угольника с единичным радиусом (расстоянием от центра до любой вершины),
называя её “очевидно… ещё одним очком в пользу \( \pi \).” Но использование формулы двойного угла \( \sin\theta\cos\theta = \frac{1}{2} \sin 2\theta \) показывает, что эта формула может быть записана как:
что просто-напросто
Другими словами, у площади \( n \)-угольника есть естественный множитель \( 1/2 \). На самом деле, решив предел в Ур. (12) при \( n\rightarrow \infty \) (и применив правило Лопиталя) получаем площадь единичного правильного многоугольника с бесконечным количеством сторон, т.е. единичную окружность:
В этом контексте мы должны заметить, что в Манифесте пи делается слишком много акцента на том, что \( \pi \) — это площадь единичного круга, из чего следует (к примеру), что квадрант (единичной) окружности — это \( \pi/4 \). Это, как говорится в Манифесте, делает \( \pi \) такой же хорошей системой измерения углов в радианах, как и \( \tau \). К сожалению для этого аргумента, как было замечено в Разделе 3 и замечено снова в Ур. (13), в контексте площади окружности множитель \( 1/2 \) появляется естественным образом. Конечно, формула площади сектора окружности, опирающегося на угол \( \theta \), равна
так что, невозможно всегда избежать множитель \( 1/2 \). (Из этого мы видим, что \( A = \frac{1}{2} \tau\, r^2 \) — это просто частный случай \( \theta = \tau \).)
Вкратце, разница между углом и площадью не произвольна. В случае с измерением углов не существует естественного множителя \( 1/2 \). По сравнению с углами, в контексте площади множитель \( 1/2 \) появляется через интеграл линейной функции, соответствующей простой квадратичной форме. На самом деле, аргументы в пользу \( \pi \) ещё хуже, чем они уже кажутся, как и будет продемонстрировано в следующем разделе.
5 Тщательное изучение пи и тау
Я продолжаю удивляться тому, насколько богата вся эта тема, и моё понимание \( \pi \) и \( \tau \) продолжает улучшаться. На "День половины тау" в 2012 году я понял, что нашёл в точности, что не так с \( \pi \). Мой аргумент стоял на анализе площади и объёма \( n \)-мерной сферы, который (как будет показано далее) делает ясным факт того, что у \( \pi \) нет никакой фундаментальной геометрической важности. Мой анализ был неполон — факт, на который мне указал читатель Манифеста тау Джефф Корнелл. Как следствие, этот раздел — это моя попытка не только окончательно опровергнуть \( \pi \), но и также артикулировать истину о \( \tau \), истину, которая глубже и тоньше, чем я до этого себе воображал.
Заметка: Этот раздел сложнее, чем остальная часть Манифеста, и может быть пропущен без потери непрерывности данного Манифеста. Если для вас этот раздел покажется непонятным, я рекомендую сразу перейти к заключению в Разделе 6.
5.1 Площадь поверхности и объём гиперсферы
Мы начнём наше расследование с обобщения окружности до произвольных измерений.16 Этот объект, называемый гиперсферой или \( n \)-сферой, может быть определён следующим образом.17 (Для удобства, мы предполагаем, что эти сферы находятся в начале координат.) \( 0 \)-сфера — это пустое множество, и мы определим её "внутренность" как точку.18\( 1 \)-сфера — это множество всех точек, удовлетворяющих
которое состоит из двух точек \( \pm r \). Её внутренность, которая удовлетворяет
это отрезок от \( -r \) до \( r \). \( 2 \)-сфера — это окружность, являющаяся множеством всех точек, удовлетворяющих
Её внутренность, которая удовлетворяет
это круг. Так же, \( 3 \)-сфера удовлетворяет
и её внутренность — это шар. Обобщение до произвольного \( n \), хотя его и сложно визуализировать для \( n > 3 \), довольно простое: \( n \)-сфера — это множество точек, удовлетворяющих
Манифест пи (обсуждаемый в Разделе 4.2) упоминает формулу объёма единичной \( n \)-сферы, как аргумент в пользу \( \pi \):
где гамма-функция задана Ур. (11). Ур. (14) представляет собой частный случай общей формулы с произвольным радиусом, которая также обычно записывается, используя \( \pi \):
Так как \( V_n(r) = \int S_n(r)\,dr \), мы получаем \( S_n(r) = dV_n(r)/dr \), означающее, что площадь поверхности может быть записана следующим образом:
Вместо того, чтобы просто принять эти формулы за чистую монету, давайте попытаемся их распутать, чтобы пролить больше света на вопрос \( \pi \) против \( \tau \). Мы начнём наш анализ с того, что заметим, что видимая простота формул сверху — это иллюзия: хотя гамма-функцию легко записать символами, она на самом деле является интегралом по полу-бесконечной области определения, что совсем не является простой идеей. К счастью, гамма-функция может быть упрощена для некоторых частных случаев. Например, когда \( n \) — целое число, легко показать (используя интегрирование по частям), что
С этой точки зрения, \( \Gamma \) может быть интерпретирована как обобщение функции факториала для вещественных аргументов.19
В формулах для площади поверхности и объёма \( n \)-сферы аргумент \( \Gamma \) не обязательно является целым числом, но \( \left(1 + \frac{n}{2}\right) \), которое является целом числом, когда \( n \) чётное число, и равно половине целого числа, когда \( n \) — нечётное. Учитывая это, получаем следующее выражение, которое взято из стандартного математического ресурса, Wolfram MathWorld, и оно как обычно записано с использованием \( \pi \):
Интегрирование по \( r \) даёт
Давайте изучим Ур. (18) более детально. Для начала обратите внимание, что MathWorld использует функцию двойного факториала \( n!! \) — но, странным образом, она используется только для нечётного случая. (Это намёк на то, что последует дальше.) Функция двойного факториала, хоть и редко встречающаяся в математике, является элементарной: она такая же, как и обычная функция факториала, но включает в себя вычитание по \( 2 \) вместо \( 1 \), так что, к примеру, \( 5!! = 5 \cdot 3 \cdot 1 \) и \( 6!! = 6 \cdot 4 \cdot 2 \). В общем, мы имеем
(По определению, \( 0!! = 1!! = 1 \).) Заметьте, как Ур. (19) естественным образом делится на чётные и нечётные частные случаи, делая ещё более загадочным тот факт, что MathWorld использует эту функцию только для нечётного случая.
Чтобы разгадать эту загадку, мы начнём с более тщательного изучения формулы для нечётных \( n \) в Ур. (18):
Проанализировав выражение
мы заметим, что его можно переписать как
и узнаём нашего старого друга \( 2\pi \).
Теперь давайте взглянем на чётный случай в Ур. (18). Сверху мы заметили странность — использование обыкновенного факториала для чётного случая и двойного факториала для нечётного случая. Так как двойной факториал уже определён частями, то, конечно, если мы объединим формулы, используя \( n!! \) в обоих случаях, мы сможем вытащить его, как общий множитель:
Так есть ли какая-либо связь между факториалом и двойным факториалом? Да. Когда \( n \) — чётное, обе функции связаны следующим уравнением:
(В этом легко убедиться с помощью математической индукции.) Подставляя это в формулу объёма для чётных \( n \), получаем
что очень сильно похоже на
и опять, мы находим ещё один множитель \( 2\pi \).
Объединив эти результаты воедино, мы видим, что Ур. (18) может быть переписано как
и Ур. (17) может быть переписано как
Делая подстановку \( \tau=2\pi \) в Ур. (21), получаем
Чтобы объединить эти формулы далее, можно использовать функцию пола\( \lfloor x \rfloor \), которая просто даёт самое большое целое число меньше или равное \( x \) (равносильно отрезанию дробной части, то есть, например, \( \lfloor 3,7 \rfloor = \lfloor 3,2 \rfloor = 3 \)). Это даёт
что позволяет нам записать формулу следующим образом:
Интегрирование Ур. (22) по \( r \) даёт нам
Лямбда
Формулы в Ур. (22) и Ур. (23) представляют собой большое улучшение над изначальной формулировкой (Ур. (17) и Ур. (18)), использовавшей \( \pi \). Но на самом деле, возможно ещё одно улучшение, используя прямой угол:20
Как мы увидим в Разделе 5.2, Ур. (24) может быть переписано в более естественной форме, используя симметрии окружности:
где множитель \( 2^2 \) появляется из-за \( 2^2 \) конгруэнтных дуг окружности (по одной из каждой четверти) в двумерном пространстве.
Самый большой плюс \( \lambda \) заключается в том, что она полностью объединяет чётные и нечётные случаи в Ур. (22) и Ур. (23), у каждого из которых есть множитель \( \tau^{\left\lfloor \frac{n}{2} \right\rfloor} \). Делая подстановку в Ур. (25), получаем
Это означает, что мы можем переписать произведение
как
что убирает явную зависимость от чётности. Применяя Ур. (26) к Ур. (22) и Ур. (23), получаем
и
Похоже, цена упрощений в Ур. (27) и Ур. (28) — это множитель \( 2^n \), но даже у него есть прозрачное геометрическое значение: сфера в \( n \) измерениях естественным образом делится на \( 2^n \) конгруэнтных кусков, соответствующих \( 2^n \) семьям решений уравнения \( \sum_{i=1}^{n} x_i^2 = r^2 \) (по одному для каждого выбора между \( \pm x_i \)). В двух измерениях это дуги окружности в каждом из четырёх квадрантов; в трёх измерениях — секторы сферы в каждой октанте; и так далее для измерений выше. Другими словами, мы можем использовать симметрию сферы в своих интересах, вычислив площадь окружности или объём одного куска — обычно главной части, где \( x_i > 0 \) для каждого \( i \) — и потом найти полное значение, умножив на \( 2^n \).
Насколько мне известно, Ур. (27) и Ур. (28) — это самые простые возможные версии формул площади поверхности и объёма сферы (и конечно единственные версии, которые я когда-либо мог хорошо запомнить). Рассмотрим, в частности, формулу объёма: несмотря на ложную простоту Ур. (15), Ур. (28) не использует никаких крутых интегралов — только немного экзотические, но всё же элементарные функции пола и двойного факториала. Объём единичной \( n \)-сферы — это просто объём каждого симметричного куска, \( \lambda^{\left\lfloor \frac{n}{2} \right\rfloor}/n!! \), умноженный на количество кусков, \( 2^n \).
Рекуррентные формулы
Мы уже увидели, благодаря Ур. (27) и Ур. (28), что формулы площади поверхности и объёма записываются в самой простой форме, используя прямой угол \( \lambda \). Тем не менее, мы ещё не закончили с \( \tau \).
Как видно из Ур. (28), формула объёма естественным образом делится на две семьи, каждая соответствует чётно- и нечётно-мерным пространствам. Это означает, что четырёхмерный объём \( V_4 \) простым образом относится к \( V_2 \) , но не к \( V_3 \), в то время как \( V_3 \) относится к \( V_1 \), но не к \( V_2 \). Как же именно они относятся друг к другу?
Мы можем найти ответ, если выведем рекуррентные отношения между измерениями.21 В частности, давайте поделим объём \( n \)-мерной сферы на объём для \( (n-2) \)-мерной сферы:
Мы видим из Ур. (29), что можем получить объём \( n \)-сферы, просто умножив формулу для \( (n-2) \)-сферы на \( r^2 \) (множитель, который требует анализ размерности), затем поделив на \( n \) и, наконец, умножив на “константу рекуррентных отношений” \( 2^2\lambda \).
Похожим образом для площади поверхности мы имеем
с такой же константой рекуррентных отношений \( 2^2\lambda \).
Таким образом, как в Ур. (29), так и в Ур. (30), константа, связывающая разные измерения, это не сама \( \lambda \), а комбинация \( 2^2\lambda \). Сравнивая с Ур. (25), мы видим, что это ничто иное как \( \tau \)! Конечно, альтернативное выведение рекуррентных отношений объёма прямым вычислением (где используется \( R \) вместо нашего \( r \)) заканчивается интегралом
таким образом показывая, что приравнивание \( \tau \) к "константе рекуррентных отношений" не совпадение — константа рекуррентных отношений и константа окружности на самом деле одно и то же:
Как следствие, это \( \tau \), а не \( \lambda \), которое является нитью, связывающей вместе две семьи чётных и нечётных решений, как показано Джозефом Линдербергом в Tau Before It Was Cool (Картинка 16).22
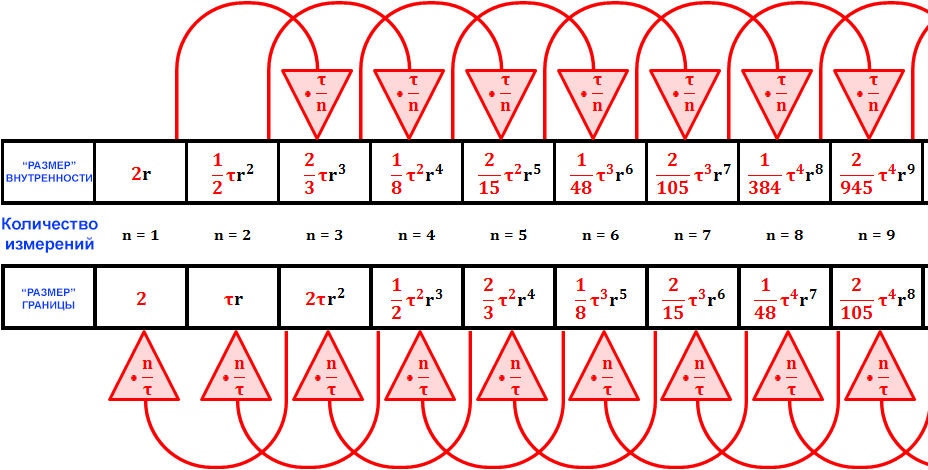
Когда мы будем обсуждать \( n \)-мерные сферы в общем, для удобства запишем формулы для площади поверхности и объёма, используя \( \lambda \), как в Ур. (27) и Ур. (28), но для любого конкретного \( n \) запишем эти результаты, используя константу рекуррентных отношений \( \tau \).
5.2 Три семьи констант
Вооружённые инструментами, разработанными в Разделе 5.1, мы в состоянии понять природу \( \pi \) и \( \tau \). Чтобы закончить наши раскопки, мы воспользуемся Ур. (27) и Ур. (28) для определения двух семей констант, а затем воспользуемся определением \( \pi \) (Ур. (1)), чтобы определить третью семью, с помощью чего показав, что на самом деле не так с \( \pi \).
Во-первых, мы определим семью "констант площади поверхности" \( \tau_n \) , разделив Ур. (27) на \( r^{n-1} \) (степень \( r \) нужна, чтобы получить безразмерную константу):
Во-вторых, мы определим семью "констант объёма" \( \sigma_n \), разделив формулу объёма Ур. (28) на \( r^n \):
С двумя семьями констант, определёнными в Ур. (32) и Ур. (33), мы можем записать формулы площади поверхности и объёма (Ур. (27) и Ур. (28)) компактно следующим образом:
и
Из отношения \( V_n(r) = \int S_n(r)\,dr \), следует простое отношение
Давайте сделаем некоторые наблюдения об этих двух семьях констант. У семьи \( \tau_n \) есть важное геометрическое значение: задав \( r=1 \) в Ур. (32), мы видим, что каждый \( \tau_n \) — это площадь поверхности единичной \( n \)-сферы, что одновременно является угловым измерением всей \( n \)-сферы. В частности, записав \( s_n(r) \) как \( n \)-мерную “длину дуги” равной доли \( f \) от полной площади поверхности \( S_n(r) \), мы получаем
Здесь \( \theta_n \) — это просто \( n \)-мерное обобщение измерения углов в радианах. Отсюда видим, что \( \tau_n \) — это обобщение “одного оборота” до \( n \) измерений, что в свою очередь объясняет, почему константа 2-сферы (окружности) \( \tau_2 = 2^2\lambda = \tau \) естественным образом ведёт к диаграмме, показанной на Картинке 10. Более того, мы поняли в Разделе 5.1, что \( \tau_2 \) также является "константой рекуррентных отношений” для площади поверхности и объёма \( n \)-сферы.
В то же время, все \( \sigma_n \) — это объёмы единичных \( n \)-сфер. В частности, \( \sigma_2 \) — это площадь единичного круга:
Это показывает, что у \( \sigma_2 = \tau/2 = 3,14159\ldots \) на самом деле есть независимый геометрический смысл. Всё же заметьте, что у этого числа нет ничего общего с длинами окружностей или диаметрами. Другими словами, \( \pi = C/D \) не является членом семьи \( \sigma_n \).
Так к какой семье констант естественным образом относится \( \pi \)? Давайте перепишем Ур. (1) в форме, наиболее подходящей для обобщения до произвольных измерений:
Таким образом, мы видим, что \( \pi \) естественным образом соответствует площадям поверхностей, поделённым на степень диаметра (необходимую чтобы получить безразмерную константу). Это приводит к созданию третьей семьи констант \( \pi_n \):
Мы можем выразить это через семью \( \tau_n \), подставив \( D = 2r \) в Ур. (34) и применив Ур. (32):
Сейчас же, наконец, понятно в точности что не так с \( \pi \). Главный геометрический смысл \( 3,14159\ldots \) заключается в том, что это площадь единичной окружности. Но это число появляется от нахождения значения \( \sigma_n = \tau_n/n \), когда \( n=2 \):
Это на самом деле равно \( \pi_2 \):
Но это равенство — совпадение: оно происходит только, потому что \( 2^{n-1} \) равен \( n \), когда \( n=2 \) (то есть \( 2^{2-1} = 2 \)). Во всех других измерениях больше двух, \( n \) и \( 2^{n-1} \) разные числа. Другими словами, геометрическая важность \( \pi \) — результат математического совпадения.
6 Заключение
В течение последних нескольких лет я слышал много доводов против неправильности \( \pi \) и против правильности \( \tau \), так что перед тем, как я завершу наше обсуждение, позвольте мне ответить на некоторые из самых часто задаваемых вопросов.
6.1 Часто Задаваемые Вопросы
- Ты серьёзно? Конечно. Ну, мне это всё очень интересно, и иногда мой тон немного шуточный, но у меня существует серьёзная цель. Определить константу окружности как длину окружности, делённую на диаметр — это неуклюжее и запутанное решение. Хотя я бы хотел, чтобы математики поменяли своё мнение, я не очень о них беспокоюсь: они могут сами о себе позаботиться. Больше всего я беспокоюсь о новичках, так как они будут пожинать плоды: как замечено в Разделе 2.1, \( \pi \) — это педагогическая катастрофа. Попытайтесь объяснить двенадцатилетнему (или тридцатилетнему), почему угол для восьмой части окружности — один кусок пиццы — это \( \pi/8 \). Ой, погодите, я имел ввиду \( \pi/4 \). Теперь понимаете? Это безумство — сущее, чистейшее безумство.
- Как переключиться с \( \pi \) на \( \tau \)? В следующий раз, когда вы будете писать что-то, что использует константу окружности, просто скажите “Для удобства, пусть \( \tau = 2\pi \)”, и продолжайте как обычно. (Конечно, это может вызвать вопрос, “Зачем тебе так делать?”, и я признаюсь, что хорошо было бы, если бы существовал сайт, на который можно было бы указать. Вот бы только кто-нибудь написал бы, я не знаю, манифест на эту тему…) Один из способов, которым можно заставить людей использовать \( \tau \) — это начать использовать его самому.
- Не поздно ли переключаться? Нужно же будет переписывать все учебники и научные работы? Ответ "нет" на оба вопроса. Правда, есть некоторые вещи, которые, к сожалению, поменять уже нельзя. Например, выбор Бенджамина Франклина относительно знаков электронных зарядов приводит к самому известному примеру того, что электрический ток (в частности, свободные электроны в металлах) по определению положительные, в то время как носители тока отрицательные, и наоборот — таким образом, с тех пор проклиная начинающих учеников в физике путающими отрицательными знаками.23 Чтобы это поменять, нужно будет переписать все учебники (и сжечь старые), так как невозможно с первого взгляда понять, какому правилу следовать. Хотя и переопределить \( \pi \) практически невозможно, мы можем переключиться с \( \pi \) на \( \tau \) на ходу, используя подстановку
\[ \pi \leftrightarrow \textstyle{\frac{1}{2}}\tau. \]
Вся "проблема" заключается в этой механической подстановке, полностью ясной и, конечно же, полностью обратимой. Переключение с \( \pi \) на \( \tau \) может быть постепенным (в отличие от одномоментного переопределения).
- Не запутает ли использование \( \tau \) людей, особенно учеников? Если ты достаточно умён, чтобы понять радианы, ты достаточно умён, чтобы понять \( \tau \) — и почему \( \tau \) на самом деле менее путающая идея, чем \( \pi \). Также, нет ничего фундаментально путающего в том, чтобы сказать “Пусть \( \tau = 2\pi \)”; в узком понимании, — это простая подстановка. В конце концов, мы можем принять ситуацию как возможность для учителя: идея о том, что \( \pi \) может быть неправильным числом, интересна, и ученики могут попытаться перевести уравнения из своих учебников с \( \pi \) на \( \tau \), чтобы понять, какой выбор лучше.
- Важно ли это вообще? Конечно важно. Константа окружности важна. Для людей она достаточно важна, чтобы писать целые книги на эту тему, чтобы праздновать эту константу в определённый день в году, и чтобы запоминать десятки тысяч её цифр. Для меня она достаточно важна, чтобы я написал про неё целый манифест, а вам она достаточно важна, чтобы этот манифест прочитать. Именно из-за того, что константа окружности на самом деле важна, трудно признать, что текущий выбор неправильный. (Ну, как объяснить Чао Лу, поставившему мировой рекорд, что он только что вспомнил 67890 цифр половины истинной константы окружности?) Так как константа окружности важна, важен и её правильный выбор, и в этом Манифесте мы увидели, что правильный выбор — \( \tau \). Хотя у числа \( \pi \) есть большая историческая значимость, maтематическая важность \( \pi \) заключается в том, что это число равно половине \( \tau \).
- Почему изначально начали использовать \( \pi \)? Как символ, \( \pi \) был популяризирован около 300 лет назад Леонардом Эйлером (основываясь на работе Уильяма Джонса), но истоки \( \pi \)-как-числа потеряны в тумане времени. Я подозреваю, что использование \( C/D \) вместо \( C/r \) стало более популярным просто потому, что проще измерить диаметр круглого предмета, чем измерить его радиус. Но из этого не выходит хорошая математика, и я удивлён, что Архимед, известный тем, что он нашёл хорошее приближение к константе окружности, не осознал, что \( C/r \) — это более фундаментальное число. Я даже больше удивлён, что Эйлер не исправил проблему, когда у него была такая возможность; в отличие от Архимеда, у Эйлера было преимущество современной системы алгебраической записи, которая (как мы увидели, начиная с Раздела 2.1) делает отношения между окружностями и константой окружности предельно ясными. Удивительным образом, Эйлер использовал символ \( \pi \) как для \( C/D \), так и для \( C/r \) в разные времена! Как жалко, что он не стандартизировал правильный выбор.
- Почему эта тема тебе интересна? Для начала, как искателю истины мне важна правильность объяснения. Во-вторых, как преподавателю мне важна ясность идей. В-третьих, как человек, изучающий историю и человеческую натуру, я нахожу удивительным тот факт, что абсурдность с \( \pi \) лежала у всех перед носом веками, прежде чем кто-то её заметил. Более того, многие из людей, которые пропустили истинную константу окружности, одни из самых рациональных и умных, которые когда-либо жили. Что ещё может смотреть нам прямо в лицо, прося быть найденным?
- Ты, эмм..., сумасшедший? Это на самом деле не ваше дело, но нет. Не считая то, что я иногда ношу необычную обувь, по всем остальным внешним признакам я абсолютно нормален. Вы бы никогда не угадали, что в дополнение к тому, что я обыкновенный гражданин, я ещё на самом деле и пресловутый математический пропагандист.
6.2 Прими тау
Мы увидели в Манифесте тау, что единственный естественный выбор для константы окружности — это отношение длины окружности не к её диаметру, а к её радиусу. Этому числу нужно название, и я надеюсь, что вы присоединитесь ко мне и будете называть её \( \tau \):
Использование естественно, мотивация ясна, следствия глубоки. Плюс, вместе с ним ещё идёт очень крутая диаграмма (Картинка 17). Мы видим в Картинке 17 движение через янь (“светлое, белое, движение вверх”) до \( \tau/2 \) и возвращение через инь (“тёмное, чёрное, движение вниз”) обратно к \( \tau \).24 Использование \( \pi \) вместо \( \tau \) — это как янь без иня.

6.3 День тау
Манифест тау впервые был выпущен на День числа тау: 28 июня (6-й месяц, 28-е число) 2010 года. День числа тау — это время для празднования всего, связанного с математикой.25 Если вы хотите получать обновления о \( \tau \), включая оповещения о возможных будущих событиях Дня числа тау, пожалуйста, присоединитесь к почтовой рассылке Манифеста тау внизу. И если вы думаете, что круглые испечённые вкусности на день пи(рога) вкусные, только погодите — на День числа тау в два раза больше пирога!
Share the τ Manifesto
Благодарности
Сначала я хотел бы поблагодарить Боба Палэя за написание статьи “\( \pi \) Is Wrong!”. Я не помню, насколько глубоки были мои подозрения касательно \( \pi \) перед тем, как я прочёл эту статью, но “\( \pi \) Is Wrong!” определённо открыла мне глаза, и каждый раздел Манифеста тау — это моя благодарность Бобу. Я бы также хотел поблагодарить его за полезные комментарии на тему этого Манифеста.
Я думал о Манифесте тау достаточно долго, и многие идеи, представленные здесь, были разработаны во время общения с моим другом Самитом Дэфтуаром. Его идеи как преподавателя и математика различным образом повлияли на моё мышление.
Я также получил поддержку и полезную обратную связь от нескольких читателей. Я бы хотел поблагодарить Вай Харт и Майкла Блэйка за их удивительные видео, вдохновлённые \( \tau \), а также Дона "Blue" МакКонелла и Скоуну Бриттан за помощь в том, что они сделали \( \tau \) частью культуры гиков (с помощью приложения time-in-\( \tau \) -для-iPhone и часов тау, соответственно). Приятная интерпретация символа инь-яня, использованная в Манифесте тау, заслуга Питера Хэрримоэса, который (как уже было замечено выше) был единственным, кто независимо предложил использовать \( \tau \) для константы окружности. Ещё один тауист до публикации Манифеста тау, Джозеф Линдерберг, также стойко меня поддерживал, и я очень ценю его энтузиазм. Я получил несколько хороших предложений от Кристофера Олы, в частности относительно геометрической интерпретации тождества Эйлера, а на Раздел 2.3.2 про тождества Эйлера был вдохновлён отличным предложением от Тимоти "Patashu" Стайлса. Дон Блахита предвидел и вдохновил некоторую часть материала про гиперсферы, и Джон Кодегадуло собрал весь материал вместе исключительно ясным и весёлым образом. Потом Джефф Корнелл, с его замечанием о важности \( \tau/4 \) в этом контексте, потряс мою веру и взорвал мне мозг.
В конце концов, я бы хотел поблагодарить Уаятта Грина за его необычайно полезную обратную связь насчёт первой версии Манифеста перед запуском; помимо других вещей, если вам нужен кто-то, кто скажет, что "почти весь [ныне убранный] раздел 5 нужно убрать", Уаятт готов помочь.
Копирайт
Манифест тау. Копирайт © 2010–2018, автор Майкл Хартл. Электронные версии Манифеста тау доступны для приобретения через сайт продаж Манифеста тау. Пожалуйста, не стесняйтесь печатать и распространять копии Манифеста тау для школьных или схожих использований.

