Buy Print Edition

Buy the print edition of The Tau Manifesto at Amazon!

Get your own Tau Tee

Celebrate Tau Day in style with a Tau tee shirt, available only for a limited time from Teespring. Offered in both men’s sizes as well as fitted women’s.

Read the State of the Tau 2024 update | Join the Tau Email List

El Manifiesto Tau

Michael HartlTraducido por Juan Guijarro Ferreiro

En el Día de Tau, 2010actualizado el Día de Tau, 2023

1 La constante de la circunferencia

El Manifiesto Tau está dedicado a uno de los números más importantes en matemáticas, quizá el más importante: la constante de la circunferencia, que relaciona su perímetro con su dimensión lineal. Desde hace miles de años se ha considerado a la circunferencia como la más perfecta de todas las formas, y esta constante condensa su geometría en un único número. Evidentemente, la opción tradicional para la constante de la circunferencia ha sido $ \pi $ (pi) pero, como señala el matemático Bob Palais en su delicioso artículo “$ \pi $ Is Wrong!”¹, $ \pi $ es un error. Es hora de hacer justicia.

1.1 Una propuesta poco modesta

Comencemos a reparar el daño que ha provocado $ \pi $ tratando de comprender en primer lugar el famoso número en sí. La definición tradicional para la constante de la circunferencia establece que $ \pi $ es la razón entre el perímetro de una circunferencia y su diámetro²:

\begin{equation} \label{eq:pi} \pi \equiv \frac{C}{D} = 3{,}14159265\ldots \end{equation}

El número $ \pi $ tiene muchas propiedades notables (entre otras cosas, es un número irracional y de hecho trascendente) y aparece por doquier en fórmulas matemáticas.

Anatomía de una circunferencia.

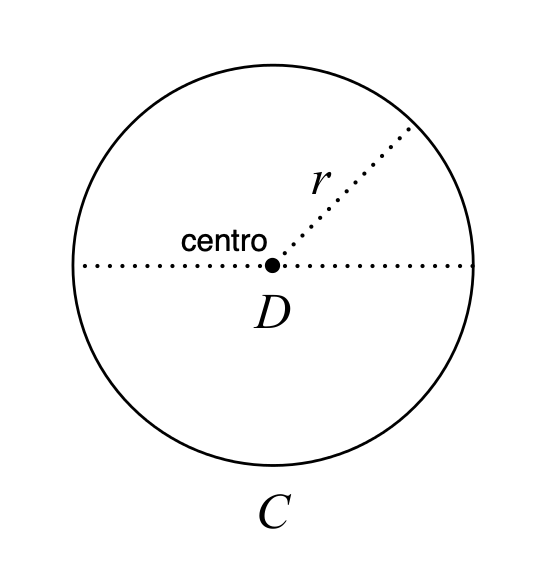
Es obvio que $ \pi $ no es “un error” en el sentido de ser factualmente incorrecto; el número $ \pi $ está perfectamente bien definido y posee todas las propiedades que las y los matemáticos habitualmente le atribuyen. Cuando decimos que “$ \pi $ es un error” queremos decir que $ \pi $ es una elección confusa y poco natural para la constante de la circunferencia. En particular, una circunferencia se define como el lugar geométrico de los puntos de un plano que se encuentran a una distancia fija, el radio, de un punto dado, el centro (figura 1). Mientras que hay un número infinito de formas con anchura constante (figura 2)³, solo hay una forma con radio constante, lo cual parece sugerir que una definición más natural para la constante de la circunferencia podría utilizar $ r $ en lugar de $ D $:

\begin{equation} \label{eq:circle_constant} \mbox{constante de la circunferencia} \equiv \frac{C}{r}. \end{equation}

Como el diámetro de una circunferencia es el doble que su radio, este número es igual a $ 2\pi $. Al igual que $ \pi $, es trascendente y por tanto irracional, y (como veremos en la sección 2) su uso en matemáticas está igualmente extendido.

Una de las infinitas formas no circulares con anchura constante.

En “$ \pi $ Is Wrong!”, Bob Palais razona persuasivamente a favor de la segunda de estas dos definiciones de la constante de la circunferencia, y desde mi punto de vista él merece todo el reconocimiento por haber identificado el problema y haberlo hecho llegar al público en general. Palais denominó a la verdadera constante de la circunferencia “una vuelta”, y también introdujo un nuevo símbolo para representarla (figura 3). Como veremos, su descripción es clarividente, pero desafortunadamente el símbolo que propuso es un poco extraño y (como se discute en la sección 4) parece poco probable que pueda ser adoptado de manera generalizada (actualización: así ha sido de hecho, y el propio Palais se ha convertido desde entonces en un firme defensor de los argumentos de este manifiesto).

El extraño símbolo para la constante de la circunferencia de “$ \pi $ Is Wrong!”.

El Manifiesto Tau está dedicado a defender que la respuesta apropiada a “$ \pi $ es un error” es “que sí, en serio”. Y la verdadera constante de la circunferencia merece un nombre adecuado. Como ya habrás podido suponer, El Manifiesto Tau propone que ese nombre sea la letra griega $ \tau $ (tau):

\begin{equation} \label{eq:tau} \tau \equiv \frac{C}{r} = 6{,}283185307179586\ldots \end{equation}

A lo largo del resto de este manifiesto, veremos que el número $ \tau $ es la opción correcta y trataremos de mostrar a través del uso (sección 2 y sección 3) y de manera directa, mediante argumentación, (sección 4) que la letra $ \tau $ también es una elección natural.

1.2 Un poderoso enemigo

Antes de empezar a demostrar que $ \tau $ es la opción natural para la constante de la circunferencia, reconozcamos primero a quién nos enfrentamos; y es que desde hace cientos de años existe una poderosa conspiración decidida a difundir propaganda pro-$ \pi $. Se escriben libros enteros para alabar las virtudes de $ \pi $ (en serio, ¡libros!). Y la devoción irracional por $ \pi $ se ha extendido hasta los más altos niveles de frikismo; por ejemplo, en el “Día de Pi” de 2010, Google cambió su logo en honor a $ \pi $ (figura 4).

El logo de Google el día 14 de marzo (3/14, en notación estadounidense) de 2010, (el “Día de Pi”).

Mientras tanto, hay personas que memorizan docenas, cientos o incluso miles de dígitos de este número místico. ¿Qué clase de persona patética hay que ser para memorizar 40 dígitos de $ \pi $ (figura 5)?⁴

Matt Groening recita incorrectamente $ \pi $ y dice “¡demostrad que me equivoco!”, así que eso hago.

Ciertamente, las personas partidarias de $ \tau $ nos enfrentamos a un imponente adversario. Y sin embargo, contamos con una poderosa aliada, pues la verdad está de nuestra parte.

2 El número tau

En la sección 1.1 vimos que el número $ \tau $ se puede escribir también como $ 2\pi $. Como se señala en “$ \pi $ Is Wrong!”, resulta por tanto de gran interés descubrir que la combinación $ 2\pi $ se encuentra con asombrosa frecuencia en todas las ramas de las matemáticas. Considérense, por ejemplo, las integrales espaciales en coordenadas polares:

\[ \int_0^{2\pi}\int_0^\infty f(r, \theta)\, r\, dr\, d\theta. \]

El límite superior de integración de la variable $ \theta $ siempre es $ 2\pi $. Aparece el mismo factor en la definición de la distribución gaussiana (normal),

\[ \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}, \]

y nuevamente en la transformada de Fourier,

\[ f(x) = \int_{-\infty}^\infty F(k)\, e^{2\pi ikx}\,dk \]

\[ F(k) = \int_{-\infty}^\infty f(x)\, e^{-2\pi ikx}\,dx. \]

Reaparece también en la fórmula integral de Cauchy,

\[ f(a) = \frac{1}{2\pi i}\oint_\gamma\frac{f(z)}{z-a}\,dz, \]

en las $ n $-ésimas raíces de la unidad,

\[ z^n = 1 \Rightarrow z = e^{2\pi i/n}, \]

y en los valores de la función zeta de Riemann para enteros positivos pares⁵:

\[ \begin{split} \zeta(2n) & = \sum_{k=1}^\infty \frac{1}{k^{2n}} \\ & = \frac{|B_{2n}|}{2(2n)!}\,(2\pi)^{2n},\qquad n = 1, 2, 3\ldots \end{split} \]

Estas fórmulas no están cuidadosamente elegidas a propósito: abre por cualquier página al azar tu libro favorito de física o matemáticas y compruébalo por ti misma. Hay muchos más ejemplos, pero en todo caso la conclusión está clara: $ 2\pi $ tiene algo de peculiar.

Para llegar al fondo de este misterio debemos volver a ciertos principios fundamentales y analizar la naturaleza de las circunferencias y especialmente la naturaleza de los ángulos. Aunque es probable que la mayor parte de este material resulte familiar merece la pena recordarlo, ya que es aquí donde comienza la verdadera comprensión de $ \tau $.

2.1 Circunferencias y ángulos

Existe una íntima relación entre circunferencias y ángulos, tal y como muestra la figura 6. Como las circunferencias concéntricas de la figura 6 tienen radios diferentes, las líneas del dibujo cortan distintas longitudes de arco, pero el ángulo $ \theta $ (theta) es el mismo en ambos casos. En otras palabras, el tamaño de los ángulos no depende del radio de la circunferencia empleada para definir el arco. La tarea principal de la medida de ángulos es crear un sistema que condense esta invarianza con respecto al radio.

Un ángulo $ \theta $ con dos circunferencias concéntricas.

Quizá el sistema de ángulos más rudimentario es el basado en grados, que divide una circunferencia en 360 partes iguales. De este sistema resulta el conjunto de ángulos especiales (familiares para quienes estudian trigonometría) que muestra la figura 7.

Algunos ángulos especiales, en grados.

Existe otro sistema más fundamental de medida de ángulos que consiste en comparar directamente la longitud de arco $ s $ y el radio $ r $. Aunque las longitudes de la figura 6 son diferentes, la longitud de arco crece en proporción al radio, de manera que el cociente entre la longitud de arco y el radio es el mismo en ambos casos:

\[ s\propto r \Rightarrow \frac{s_1}{r_1} = \frac{s_2}{r_2}. \]

Esto sugiere la siguiente definición de medida de ángulos en radianes:

\begin{equation} \label{eq:radians} \theta \equiv \frac{s}{r}. \end{equation}

Esta definición posee la propiedad requerida de ser invariante con respecto al radio, y dado que tanto $ s $ como $ r $ tienen unidades de longitud, los radianes son adimensionales por construcción. Medir ángulos en radianes produce fórmulas concisas y elegantes en matemáticas; por ejemplo, la fórmula habitual para la derivada de $ \sen\theta $ es cierta solamente cuando $ \theta $ se expresa en radianes:

\[ \frac{d}{d\theta}\mbox{sen}\,\theta = \cos\theta \qquad\mbox{(solo en radianes).} \]

Naturalmente, los ángulos especiales de la figura 7 se pueden expresar en radianes, y cuando aprendiste trigonometría en secundaria probablemente tuviste que memorizar los valores especiales que se muestran en la figura 8 (denomino a esta unidad de medida $ \pi $-radianes para enfatizar que están escritos en términos de $ \pi $).

Algunos ángulos especiales, en $ \pi $-radianes.

$images/figures/angle-fractions$

Los ángulos “especiales” como fracciones de una circunferencia completa.

Si lo pensamos por un momento, vemos que estos ángulos “especiales” no son más que fracciones racionales particularmente sencillas de una circunferencia completa, como se muestra en la figura 9. Esto invita a revisar la ecuación (4), reescribiendo la longitud del arco $ s $ en función de la fracción $ f $ de la circunferencia completa $ C $, es decir, $ s = f C $:

\begin{equation} \label{eq:circle_fraction} \theta = \frac{s}{r} = \frac{fC}{r} = f\left(\frac{C}{r}\right) \equiv f\tau. \end{equation}

Nótese cuán naturalmente se desprende $ \tau $ de este análisis. Si eres una persona creyente en $ \pi $, me temo que el diagrama de ángulos especiales resultante (figura 10) va a sacudir tu fe desde sus entrañas.

Algunos ángulos especiales, en radianes.

Aunque hay muchos otros argumentos a favor de $ \tau $, puede que la figura 10 sea el más impactante. En la figura 10 vemos también la genialidad de Bob Palais al identificar la constante de la circunferencia como “una vuelta”: $ \tau $ es la medida de ángulo en radianes para una vuelta de circunferencia. Es más: nótese que con $ \tau $ no hay nada que memorizar: la duodécima parte de una vuelta es $ \tau/12 $, la octava parte de una vuelta es $ \tau/8 $, y así sucesivamente. Utilizar $ \tau $ nos da lo mejor de ambos mundos, combinando claridad conceptual con todos los beneficios específicos de los radianes; el significado abstracto de, por ejemplo, $ \tau/12 $ es obvio, pero también es simplemente un número:

\[ \begin{split} \mbox{duodécima parte de una vuelta} = \frac{\tau}{12} & \approx \frac{6{,}283185}{12} \\ & = 0{,}5235988. \end{split} \]

Por último, si comparamos la figura 8 con la figura 10, vemos de dónde proceden esos engorrosos factores de $ 2\pi $: una vuelta de circunferencia es $ 1\tau $, pero $ 2\pi $. Numéricamente son iguales, pero conceptualmente son bien distintos.

Las consecuencias

Esos innecesarios factores de $ 2 $ que se derivan del uso de $ \pi $ son bastante molestos por sí mismos, pero más grave aún es su tendencia a cancelarse cuando se dividen por cualquier número par. Se producen resultados absurdos, como la mitad de $ \pi $ para un cuarto de vuelta, que ocultan la relación subyacente entre la medida de un ángulo y la constante de la circunferencia. A quienes sostienen que “da igual” utilizar $ \pi $ o $ \tau $ al enseñar trigonometría solo les pido que traten de ver la figura 8, la figura 9 y la figura 10 a través de los ojos de un niño o niña. Verán que, desde la perspectiva de alguien que empieza a aprender, usar $ \pi $ en lugar de $ \tau $ es un desastre pedagógico.

2.2 Las funciones circulares

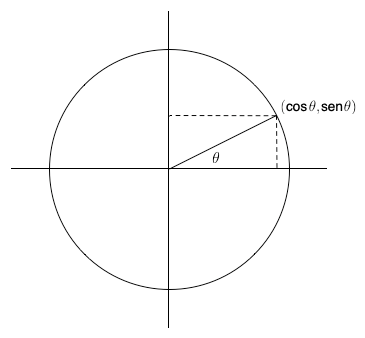
Aunque la medida de ángulos en radianes ofrece algunos de los argumentos más convincentes sobre la constante de la circunferencia, también vale la pena comparar las virtudes de $ \pi $ y $ \tau $ en otros contextos. Empecemos por considerar las importantes funciones básicas $ \sen\theta $ y $ \cos\theta $. Conocidas como “funciones circulares” por representar las coordenadas de un punto en la circunferencia unitaria (es decir, una circunferencia con radio $ 1 $), el seno y el coseno son funciones fundamentales en trigonometría (figura 11).

Las funciones circulares son coordenadas en la circunferencia unitaria.

Examinemos las gráficas de las funciones circulares para comprender mejor su comportamiento⁶. En la figura 12 y la figura 13 se observa que ambas funciones son periódicas con periodo $ T $. Como se muestra en la figura 12, la función $ \sen\theta $ comienza en cero, alcanza un máximo al llegar a un cuarto del periodo, pasa por cero en la mitad del periodo, alcanza un mínimo en las tres cuartas partes del periodo y vuelve a cero tras un periodo completo. Por su parte, la función $ \cos\theta $ comienza en un máximo, tiene un mínimo en la mitad del periodo y pasa por cero en un cuarto y tres cuartos del periodo (figura 13). A modo de referencia, ambas figuras muestran el valor de $ \theta $ (en radianes) en cada punto especial.

Puntos importantes de $ \sen\theta $ en relación con el periodo $ T $.

Puntos importantes de $ \cos\theta $ en relación con el periodo $ T $.

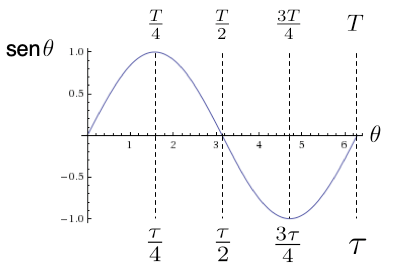
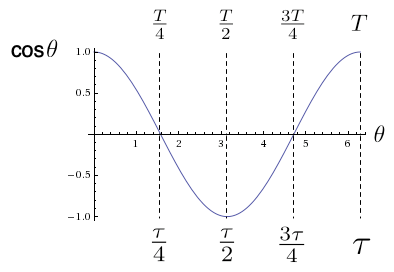
Por supuesto, dado que tanto seno como coseno completan un ciclo completo tras una vuelta alrededor de la circunferencia, tenemos que $ T = \tau $; es decir, las funciones circulares tienen periodos iguales a la constante de la circunferencia. Como consecuencia, los valores “especiales”de $ \theta $ son completamente naturales: un cuarto del periodo es $ \tau/4 $, la mitad del periodo es $ \tau/2 $, etc. De hecho, cuando estaba creando la figura 12 me encontré en un momento dado pensando en cuál sería el valor numérico de $ \theta $ para el cero de la función seno. Dado que el cero se produce tras medio periodo, y dado que $ \tau \approx 6{,}28 $, un cálculo mental rápido me condujo al siguiente resultado:

\[ \theta_\mathrm{cero} = \frac{\tau}{2} \approx 3{,}14. \]

Así es: me quedé atónito al descubrir que ya había olvidado que a veces $ \tau/2 $ se llama “$ \pi $”. Quizá incluso te acaba de pasar lo mismo a ti. Bienvenido o bienvenida a mi mundo.

2.3 La identidad de Euler

Sería un descuido por mi parte no abordar la identidad de Euler, algunas veces calificada como “la ecuación más hermosa de las matemáticas”. Esta identidad utiliza la exponencial compleja, que está profundamente conectada tanto con la constante de la circunferencia como con su misma geometría.

Dependiendo del camino elegido, la siguiente ecuación puede demostrarse como teorema o tomarse como definición; en cualquier caso, es realmente excepcional:

\begin{equation} \label{eq:eulers_formula} e^{i\theta} = \cos\theta + i\,\sen\theta \qquad\mbox{Fórmula de Euler.} \end{equation}

Conocida como la fórmula de Euler (en honor a Leonhard Euler), esta ecuación relaciona una exponencial con argumento imaginario con las funciones circulares seno y coseno y con la unidad imaginaria $ i $. Aunque explicar la fórmula de Euler queda fuera del alcance de este manifiesto, su origen no es precisamente sospechoso, y su importancia es incuestionable.

Si evaluamos la ecuación (6) en $ \theta = \tau $ obtenemos

\begin{equation} \label{eq:eulers_identity_tau_0i} e^{i\theta} = \cos\theta + i\,\sen\theta = 1 + 0i\, \end{equation}

que se simplifica para dar como resultado la identidad de Euler⁷:

\begin{equation} \label{eq:eulers_identity_tau} e^{i\tau} = 1 \qquad\mbox{Identidad de Euler (versión con $\tau$).} \end{equation}

Expresada en palabras, la ecuación (8) realiza la siguiente observación fundamental:

La exponencial compleja de la constante de la circunferencia es la unidad.

Geométricamente, multiplicar por $ e^{i\theta} $ equivale a rotar un número complejo un ángulo $ \theta $ en el plano complejo, lo que sugiere una segunda interpretación de la identidad de Euler:

Una rotación de una vuelta es 1.

Dado que el número $ 1 $ es la identidad multiplicativa, el significado geométrico de $ e^{i\tau} = 1 $ es que rotar un punto en el plano complejo una vuelta completa simplemente lo devuelve a su posición original.

Como en el caso de la medida de ángulos en radianes, vemos lo natural que resulta la asociación entre $ \tau $ y una vuelta alrededor de una circunferencia. Tanto es así, que la identificación de $ \tau $ con “una vuelta” hace que la identidad de Euler suene casi como una tautología.

No precisamente la ecuación más hermosa

La forma tradicional de la ecuación de Euler se escribe, por supuesto, en términos de $ \pi $ en lugar de $ \tau $. Para obtenerla, comenzamos por evaluar la fórmula de Euler en $ \theta = \pi $, lo que produce

\begin{equation} \label{eq:eulers_identity_pi_unsimplified} e^{i\pi} = \cos \pi + i \sen \pi = -1 + 0i \end{equation}

y se simplifica a:

\begin{equation} \label{eq:eulers_identity_pi} e^{i\pi} = -1 \qquad\mbox{Identidad de Euler (con $\pi$).} \end{equation}

Pero ese signo menos es tan feo que la ecuación (10) casi siempre se reordena inmediatamente, produciendo la siguiente “hermosa” ecuación:

\begin{equation} \label{eq:eulers_pi_rearranged} e^{i\pi} + 1 = 0 \qquad\mbox{(reordenada).} \end{equation}

Al llegar a este punto, la persona que diserta habitualmente efectúa alguna afirmación numerológica grandilocuente sobre cómo la ecuación (11) identidad de Euler relaciona $ 0 $, $ 1 $, $ e $, $ i $ y $ \pi $, en ocasiones llamados los “cinco números más importantes de las matemáticas”.

Es impresionante la cantidad de gente que se queja de que la identidad de Euler con $ \tau $ solo relaciona cuatro de estos cinco. De acuerdo:

\begin{equation} \label{eq:eulers_tau_zero} e^{i\tau} = 1 + 0. \end{equation}

De hecho, ya vimos en la ecuación (7) que en realidad hay un $ 0i $ incluido (procedente de $ i \sen\tau $):

\begin{equation} \label{eq:eulers_tau_zero_i} e^{i\tau} = 1 + 0i. \end{equation}

La ecuación (13), sin reordenar, relaciona ciertamente los presuntos cinco números más importantes de las matemáticas: $ 0 $, $ 1 $, $ e $, $ i $ y $ \tau $.

Identidades eulerianas

Dado que es posible añadir cero en cualquier ecuación, introducir $ 0 $ en la ecuación (12) no deja de ser un contrapunto irónico a $ e^{i\pi} + 1 = 0 $, pero realmente puede extraerse algo importante de la identidad $ e^{i\pi} = -1 $. Veamos qué sucede cuando la reescribimos en términos de $ \tau $:

\[ e^{i\tau/2} = -1. \]

Geométricamente, esto significa que una rotación de media vuelta es lo mismo que multiplicar por $ -1 $. Y efectivamente, así es: tras una rotación de $ \tau/2 $ radianes, el número complejo $ z = a + ib $ queda asignado a $ -a - ib $, que es de hecho $ -1\cdot z $.

Escrita en términos de $ \tau $, vemos que la forma “original” de la identidad de Euler (ecuación (10)) tiene un significado geométrico obvio del que carece cuando se escribe en términos de $ \pi $ (por supuesto, $ e^{i\pi} = -1 $ se puede interpretar como una rotación por $ \pi $ radianes, pero la casi universal reordenación a la forma $ e^{i\pi} + 1 = 0 $ evidencia cómo el uso de $ \pi $ desvía la atención del significado geométrico natural de la identidad). Las identidades de cuartos de ángulo tienen interpretaciones geométricas similares: evaluar la ecuación (6) en $ \tau/4 $ nos da $ e^{i\tau/4} = i $, que significa que un cuarto de vuelta en el plano complejo es lo mismo que multiplicar por $ i $; igualmente, $ e^{i\cdot(3\tau/4)} = -i $ quiere decir que tres cuartos de vuelta es lo mismo que multiplicar por $ -i $. La tabla 1 presenta un resumen de estos resultados, que denominaremos identidades eulerianas.

Ángulo de rotación	Identidad euleriana
$ 0 $	$ e^{i\cdot0} $	$ = $	$ 1 $
$ \tau/4 $	$ e^{i\tau/4} $	$ = $	$ i $
$ \tau/2 $	$ e^{i\tau/2} $	$ = $	$ -1 $
$ 3\tau/4 $	$ e^{i\cdot(3\tau/4)} $	$ = $	$ -i $
$ \tau $	$ e^{i\tau} $	$ = $	$ 1 $

Identidades eulerianas para rotaciones de cuartos de vuelta, media vuelta y vuelta completa.

Podemos llevar este análisis un paso más allá señalando que, para cualquier ángulo $ \theta $, se puede interpretar $ e^{i\theta} $ como un punto perteneciente a la circunferencia unidad en el plano complejo. Como el plano complejo identifica el eje horizontal con la parte real del número y el eje vertical con la parte imaginaria, la fórmula de Euler nos dice que $ e^{i\theta} $ son las coordenadas $ (\cos\theta, \sen\theta) $. Si introducimos los valores de los ángulos “especiales” de la figura 10 en la ecuación (6) obtenemos los puntos de la tabla 2, y si dibujamos estos puntos en el plano complejo obtenemos la figura 14. Una comparación entre la figura 14 y la figura 10 disipa rápidamente cualquier duda acerca de cuál de las constantes de la circunferencia revela mejor la relación entre la fórmula de Euler y la geometría del círculo.

Forma polar	Forma rectangular	Coordenadas
$ e^{i\theta} $	$ \cos\theta + i\,\sen\theta $	$ (\cos\theta, \sen\theta) $
$ e^{i\cdot0} $	$ 1 $	$ (1, 0) $
$ e^{i\tau/12} $	$ \frac{\sqrt{3}}{2} + \frac{1}{2}i $	$ (\frac{\sqrt{3}}{2}, \frac{1}{2}) $
$ e^{i\tau/8} $	$ \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i $	$ (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) $
$ e^{i\tau/6} $	$ \frac{1}{2} +\frac{\sqrt{3}}{2} i $	$ (\frac{1}{2}, \frac{\sqrt{3}}{2}) $
$ e^{i\tau/4} $	$ i $	$ (0, 1) $
$ e^{i\tau/3} $	$ -\frac{1}{2} +\frac{\sqrt{3}}{2} i $	$ (-\frac{1}{2}, \frac{\sqrt{3}}{2}) $
$ e^{i\tau/2} $	$ -1 $	$ (-1, 0) $
$ e^{i\cdot(3\tau/4)} $	$ -i $	$ (0, -1) $
$ e^{i\tau} $	$ 1 $	$ (1, 0) $

Exponenciales complejas de los ángulos especiales de la figura 10.

Exponenciales complejas de algunos ángulos especiales dibujados en el plano complejo.

3 El área del círculo: el tiro de gracia

Si has llegado aquí como creyente en $ \pi $, a estas alturas probablemente estarás poniendo en duda tu fe. $ \tau $ es tan natural, su significado tan obvio... ¿No hay ningún ejemplo en que $ \pi $ brille en toda su resplandeciente gloria? Se agita un recuerdo —sí, existe tal fórmula—, ¡es la fórmula del área del círculo! Contemplad:

\[ A = \tfrac{1}{4} \pi D^2. \]

No, espera. La fórmula del área siempre se escribe en términos del radio, así:

\[ A = \pi r^2. \]

Aquí vemos a $ \pi $, sin adornos, en una de las ecuaciones más importantes en matemáticas: una fórmula demostrada por primera vez por el mismísimo Arquímedes. ¡Queda restablecido el orden! Y sin embargo, el nombre de este epígrafe suena funesto… Si esta ecuación es la gloriosa coronación de $ \pi $, ¿cómo puede ser también su tiro de gracia?

3.1 Formas cuadráticas

Examinemos este presunto modelo ejemplar de $ \pi $, $ A = \pi r^2 $. Observamos que contiene el radio elevado a la segunda potencia. Esto lo convierte en una sencilla forma cuadrática. Estas formas surgen en muchos contextos; como físico, mis ejemplos favoritos provienen de las asignaturas de la carrera de física. Vamos a examinar unos cuantos de estos ejemplos.

Caída libre en un campo gravitacional uniforme

Galileo Galilei descubrió que la velocidad de un objeto que cae en un campo gravitacional uniforme es proporcional a su tiempo de caída:

\[ v \propto t. \]

La constante de proporcionalidad es la aceleración gravitacional $ g $:

\[ v = g t. \]

Como la velocidad es la derivada de la posición, podemos calcular la distancia recorrida por integración⁸:

\[ y = \int v\,dt = \int_0^t gt\,dt = \textstyle{\frac{1}{2}} gt^2. \]

Energía potencial en un muelle lineal

Robert Hooke descubrió que la fuerza externa requerida para estirar un muelle es proporcional a su elongación:

\[ F \propto x. \]

La constante de proporcionalidad es la constante elástica del muelle $ k $⁹:

\[ F = k x. \]

La energía potencial del muelle es por tanto igual al trabajo realizado por la fuerza externa:

\[ U = \int F\,dx = \int_0^x kx\,dx = \textstyle{\frac{1}{2}} kx^2. \]

Energía del movimiento

Isaac Newton descubrió que la fuerza ejercida sobre un objeto es proporcional a su aceleración:

\[ F \propto a. \]

La constante de proporcionalidad es la masa $ m $:

\[ F = m a. \]

La energía del movimiento, o energía cinética, es igual al total del trabajo invertido en acelerar la masa hasta la velocidad $ v $:

\[ \begin{split} K = \int F\,dx = \int ma\,dx & = \int m\frac{dv}{dt}\,dx \\ & = \int m\frac{dx}{dt}\,dv \\ & = \int_0^v mv\,dv \\ & = \textstyle{\frac{1}{2}} mv^2. \end{split} \]

3.2 Un presentimiento

Tras haber visto varios ejemplos de formas cuadráticas simples en física, es posible que hayas sentido un presentimiento ahora que volvemos a la geometría de la circunferencia. Hay motivos para ello.

Descomposición de un círculo en anillos.

Como se puede observar en la figura 15, el área de un círculo se puede calcular descomponiéndolo en anillos circulares de longitud $ C $ y anchura $ dr $, de manera que el área de cada anillo es $ C\,dr $:

\[ dA = C\,dr. \]

Bien, tenemos que la longitud de una circunferencia es proporcional a su radio:

\[ C \propto r. \]

La constante de proporcionalidad es $ \tau $:

\[ C = \tau\,r. \]

El área de un círculo, por tanto, es la integral de todos los anillos:

\[ A = \int dA = \int_0^r C\,dr = \int_0^r \tau\,r\,dr = \textstyle{\frac{1}{2}} \tau\,r^2. \]

Si aún eras partidaria o partidario acérrimo de $ \pi $ al comienzo de esta sección, ahora te habrá explotado la cabeza. Y es que vemos que aún en este caso, donde supuestamente $ \pi $ debía resplandecer, en realidad se ha perdido un factor de $ 2 $. De hecho, la demostración original de Arquímedes no muestra que el área de un círculo sea $ \pi r^2 $, sino que es igual al área de un triángulo rectángulo de base $ C $ y altura $ r $. Si aplicamos la fórmula para áreas de triángulos obtenemos

\[ A = \textstyle{\frac{1}{2}} bh = \textstyle{\frac{1}{2}}Cr = \textstyle{\frac{1}{2}}\tau\,r^2. \]

Sencillamente, no hay manera de evitar ese factor de un medio (tabla 3).

Cantidad	Símbolo	Expresión
Distancia en caída	$ y $	$ \textstyle{\frac{1}{2}}gt^2 $
Energía del muelle	$ U $	$ \textstyle{\frac{1}{2}}kx^2 $
Energía cinética	$ K $	$ \textstyle{\frac{1}{2}}mv^2 $
Área del círculo	$ A $	$ \textstyle{\frac{1}{2}}\tau\,r^2 $

Algunas formas cuadráticas habituales.

Quod erat demonstrandum

En este manifiesto nos propusimos exponer que $ \tau $ es la verdadera constante de la circunferencia. Dado que la fórmula del área del círculo era más o menos el último y mejor argumento que le quedaba a $ \pi $ , me la voy a jugar ya mismo y voy a decir: Q.E.D.

4 Conflicto y resistencia

A pesar de esta decisiva demostración de su superioridad, hay muchas personas que se oponen a $ \tau $, como notación y como número. En esta sección abordaremos las inquietudes de quienes aceptan el valor pero no la letra. Después refutaremos algunos de los muchos argumentos reunidos contra $ C/r $, incluyendo el llamado “Manifiesto Pi” que defiende la superioridad de $ \pi $. A continuación, discutiremos el relativamente avanzado asunto del volumen de una hiperesfera (sección 5.1), que mejora y amplía los argumentos de la sección 3 sobre el área del círculo.

4.1 Una vuelta

La verdadera prueba que debe superar cualquier notación es el uso; después de haber visto la letra $ \tau $ en uso a lo largo de todo este manifiesto, es posible que te haya convencido de que sirve bien a su propósito. Pero en el caso de una constante tan fundamental como $ \tau $ estaría bien tener razones más profundas para su elección. ¿Por qué no $ \alpha $, por ejemplo, u $ \omega $? ¿Qué tiene $ \tau $ de especial?

Hay dos razones principales para utilizar $ \tau $ para representar la constante de la circunferencia. La primera es que $ \tau $ se parece visualmente a $ \pi $: tras siglos de uso, la asociación de $ \pi $ con la constante de la circunferencia es inevitable, y el empleo de $ \tau $ se nutre de esta asociación en lugar de combatirla (de hecho, la línea horizontal en ambas letras sugiere que interpretemos las “patas” como denominadores, de manera que $ \pi $ tiene dos patas en su denominador y $ \tau $ solo una. Visto de esta forma, la relación $ \tau = 2\pi $ resulta perfectamente natural)¹⁰.

La segunda razón es que $ \tau $ se corresponde con una vuelta (N. del T.: en inglés, “turn”) alrededor de una circunferencia, y puede que hayas observado que tanto “$ \tau $” como “turn” comienzan con sonido de “t”. Este fue el motivo original para la elección de $ \tau $, y no es una coincidencia: la raíz de la palabra inglesa “turn” es la palabra griega τόρνος (tornos), que significa “torno”. Si utilizamos una tipografía matemática para la primera letra de τόρνος tenemos $ \tau $.

Desde la presentación original de El Manifiesto Tau, he descubierto que Peter Harremoës propuso de manera independiente utilizar $ \tau $ a Bob Palais, autor de “$ \pi $ Is Wrong!”, en 2010, que John Fisher propuso usar $ \tau $ en una publicación en Usenet en 2004, ¡y que Joseph Lindenberg anticipó tanto el debate como el símbolo más de veinte años antes¹¹! El Dr. Harremoës ha destacado la importancia de un aspecto ya presentado en la sección 1.1: emplear $ \tau $ da un nombre a la constante de la circunferencia. Dado que $ \tau $ es una letra griega común, aquellas personas que la encuentren por primera vez pueden pronunciarla inmediatamente. Y más aún: a diferencia de denominar “una vuelta” a la constante de la circunferencia, $ \tau $ funciona bien tanto en contextos escritos como orales. Por ejemplo, decir que el ángulo de un cuarto de circunferencia en radianes es “un cuarto de vuelta” en radianes suena muy bien, pero “vuelta cuartos radianes” suena forzado, y “el área de un círculo es media vuelta por $ r $ al cuadrado” suena francamente raro. Utilizando $ \tau $, podemos decir “tau cuartos radianes” y “el área de un círculo es tau medios por $ r $ al cuadrado”.

Notación ambigua

No hay duda de que cualquier notación nueva conlleva un potencial conflicto con el uso preexistente. Como se señala en la sección 1.1, “$ \pi $ Is Wrong!” evita este problema acuñando un nuevo símbolo (figura 3). Hay precedentes de esta práctica; por ejemplo, en los primeros tiempos de la mecánica cuántica Max Planck introdujo la constante $ h $, que relaciona la energía de una partícula de luz con su frecuencia (mediante $ E = h\nu $), pero el mundo de la física pronto se dio cuenta de que a menudo resultaba más cómodo utilizar $ \hbar $ (léase “hache barra”) —donde $ \hbar $ simplemente es $ h $ dividido entre… hum… $ 2\pi $— y este uso es ahora estándar.

No obstante, es difícil lograr la aceptación de un nuevo símbolo: debe dársele un nombre, ese nombre se debe popularizar y el símbolo en sí debe añadirse a los sistemas de procesamiento de textos y tipografías. Por otra parte, promulgar un nuevo símbolo para $ 2\pi $ requeriría la cooperación de la comunidad académica matemática, que en la cuestión de $ \pi $ vs. $ \tau $ ha sido hasta el momento apática en el mejor de los casos y hostil en el peor¹². Emplear un símbolo que ya existe nos facilitará brujulear en el mundo del establishment matemático¹³.

Antes que promover un símbolo nuevo, El Manifiesto Tau opta por el uso de una letra griega existente. Por ello, dado que $ \tau $ ya se utiliza en algunos contextos, debemos preocuparnos por los conflictos con la praxis actual. Por suerte hay sorprendentemente pocos usos comunes. Aún más, aunque $ \tau $ se utiliza para ciertas variables específicas (por ejemplo, tensión cortante en ingeniería mecánica, torque en mecánica rotacional y tiempo propio en relatividad especial y general) no hay ningún uso conflictivo universal¹⁴. En estos casos, podemos tolerar la ambigüedad o evitar los escasos conflictos actuales cambiando de manera selectiva la notación, usando por ejemplo $ N $ para el torque¹⁵, $ \tau_p $ para el tiempo propio o incluso $ \tau_\odot $ para la propia constante de la circunferencia.

A pesar de estos argumentos, los potenciales usos conflictivos han sido la mayor fuente de oposición a $ \tau $. Algunas personas que me han escrito han llegado a negar categóricamente que $ \tau $ (o, presumiblemente, cualquier otro símbolo actualmente en uso) vaya a poder superar estos problemas. Pero la ciencia y la ingeniería tienen una elevada tolerancia a la ambigüedad notacional, y afirmar que $ \tau $ como constante de la circunferencia no puede coexistir con otros usos ignora la existencia de una significativa evidencia en sentido contrario.

Un ejemplo de ambigüedad que se tolera tranquilamente se da en mecánica cuántica, ámbito en que encontramos la siguiente fórmula para el radio de Bohr, que es (grosso modo) el “tamaño” de un átomo de hidrógeno en su estado de mínima energía (el estado fundamental):

\begin{equation} \label{eq:bohr_radius} a_0 = \frac{\hbar^2}{m e^2}, \end{equation}

donde $ m $ es la masa del electrón y $ e $ es su carga. Por su parte, el estado fundamental en sí mismo se describe mediante una cantidad conocida como la función de onda, que decae exponencialmente con el radio en una escala de longitud establecida por el radio de Bohr:

\begin{equation} \label{eq:hydrogen} \psi(r) = N\,e^{-r/a_0}, \end{equation}

donde $ N $ es una constante de normalización.

¿Ya te has dado cuenta del problema? Probablemente no, y ese es precisamente el asunto. El “problema” es que la $ e $ en la ecuación (14) y la $ e $ en la ecuación (15) no son la misma $ e $; la primera es la carga del electrón, mientras que la segunda es el número de Euler (la base de los logaritmos naturales). De hecho, si desarrollamos el factor $ a_0 $ en el exponente en la ecuación (15), obtenemos

\[ \psi(r) = N\,e^{-m e^2 r/\hbar^2}, \]

que tiene una $ e $ elevado a algo que contiene otra $ e $ distinta. Es aún peor de lo que parece, porque la propia $ N $ también contiene a $ e $:

\[ \psi(r) = \sqrt{\frac{1}{\pi a_0^3}}\,e^{-r/a_0} = \frac{m^{3/2} e^3}{\pi^{1/2} \hbar^3}\,e^{-m e^2 r/\hbar^2}. \]

No me cabe ninguna duda de que si no hubiera existido una notación específica para el número de Euler, a cualquier persona que hubiera propuesto la letra $ e $ se le habría dicho que era imposible por entrar en conflicto con otros usos. Y a pesar de ello, en la práctica nadie ha tenido nunca ningún problema en usar $ e $ en los dos contextos arriba señalados. Hay muchos otros ejemplos, que incluyen situaciones donde incluso $ \pi $ se utiliza para dos cosas distintas¹⁶. Resulta difícil explicar por qué usar $ \tau $ para distintos números debería ser diferente.

Por cierto, los pedantes de $ \pi $ que hay por ahí (y está demostrado que hay muchos) podrían señalar que la función de onda del estado fundamental del hidrógeno tiene un factor de $ \pi $:

\[ \psi(r) = \sqrt{\frac{1}{\pi a_0^3}}\,e^{-r/a_0}. \]

A simple vista, esta forma parece más natural que la versión con $ \tau $:

\[ \psi(r) = \sqrt{\frac{2}{\tau a_0^3}}\,e^{-r/a_0}. \]

Pero como de costumbre, las apariencias engañan: el valor de $ N $ procede del producto

\[ \frac{1}{\sqrt{2\pi}} \frac{1}{\sqrt{2}} \frac{2}{a_0^{3/2}}, \]

que muestra que la constante de la circunferencia entra en el cálculo mediante la expresión $ 1/\sqrt{2\pi} $, es decir, $ 1/\sqrt{\tau} $. Como en la fórmula del área del círculo, que la cancelación deje un $ \pi $ desnudo es mera coincidencia.

4.2 El Manifiesto Pi

Aunque la mayoría de la objeciones a $ \tau $ proceden de correspondencia dispersa por correo electrónico y comentarios variados en la web, también hay una resistencia organizada. En concreto, tras la publicación de El Manifiesto Tau en junio de 2010 apareció un “Manifiesto Pi” para defender la constante de la circunferencia tradicional. Esta sección y las dos siguientes contienen una réplica a sus razonamientos¹⁷. Por necesidad, su tratamiento es más escueto y avanzado que el resto del manifiesto, pero incluso una lectura superficial de lo que sigue a continuación da una idea de la debilidad de los argumentos de El Manifiesto Pi.

Aunque ciertamente podemos considerar la aparición de El Manifiesto Pi como un signo positivo de interés sostenido en el tiempo en torno a este asunto, hace bastantes afirmaciones falsas. Por ejemplo, alega que el factor de $ 2\pi $ en la distribución gaussiana (normal) es una coincidencia, y que puede escribirse de manera más natural como

\[ \frac{1}{\sqrt\pi(\sqrt 2\sigma)}e^{\frac{-x^2}{(\sqrt 2\sigma)^2}}. \]

Esto es incorrecto: el factor de $ 2\pi $ proviene de elevar al cuadrado la distribución gaussiana no normalizada y cambiar a coordenadas polares, lo que genera un factor de $ 1 $ de la integral radial y $ 2\pi $ de la integral angular. Como en el caso del área del círculo, el factor de $ \pi $ proviene de $ 1/2\times 2\pi $, no de $ \pi $ solo.

Una afirmación relacionada es que la función gamma evaluada en $ 1/2 $ es más natural en términos de $ \pi $:

\[ \Gamma(\textstyle{\frac{1}{2}}) = \sqrt{\pi}, \]

donde

\begin{equation} \label{eq:gamma} \Gamma(p) = \int_{0}^{\infty} x^{p-1} e^{-x}\,dx. \end{equation}

Pero $ \Gamma(\frac{1}{2}) $ se reduce a la misma integral gaussiana que en la distribución normal (tras la sustitución $ u = x^{1/2} $), así que $ \pi $ en este caso es también en realidad $ 1/2\times 2\pi $. De hecho, en muchos de los casos que se citan en El Manifiesto Pi la constante de la circunferencia aparece a través de una integral sobre todos los ángulos, es decir, una integral en que $ \theta $ varía entre $ 0 $ y $ \tau $.

El Manifiesto Pi también examina algunas fórmulas de polígonos regulares de $ n $ lados (o “$ n $-ágonos”). Por ejemplo, señala que la suma de los ángulos internos de un $ n $-ágono viene dada por

\[ \sum_{i=1}^n \theta_i=(n-2)\pi. \]

Esta cuestión fue tratada en “Pi Is Wrong!”, que señala lo siguiente: “la suma de los ángulos interiores [de un triángulo] es $ \pi $, de acuerdo. Pero la suma de los ángulos exteriores de cualquier polígono, de la que la suma de los ángulos interiores se puede derivar fácilmente, y que se generaliza como la integral de la curvatura de una curva cerrada simple, es $ 2\pi $”. Además, El Manifiesto Pi presenta la fórmula del área de un $ n $-ágono con radio (distancia desde el centro hasta un vértice) unidad,

\[ A=n\,\mbox{sen}\,\frac{\pi}{n}\cos\frac{\pi}{n}, \]

que presenta como “claramente… otra victoria para $ \pi $”. Pero si utilizamos la identidad del ángulo doble $ \sen\theta\cos\theta = \frac{1}{2} \sen 2\theta $, vemos que esa expresión se puede reescribir como

\[ A = n/2\, \mbox{sen}\,\frac{2\pi}{n}, \]

que no es más que

\begin{equation} \label{eq:area_polygon} A = \frac{1}{2} n\, \mbox{sen}\,\frac{\tau}{n}. \end{equation}

En otras palabras, el área de un $ n $-ágono tiene de forma natural un factor de $ 1/2 $. De hecho, tomar el límite de la ecuación (17) cuando $ n\rightarrow \infty $ (aplicando la regla de l’Hôpital) proporciona el área de un polígono regular unitario con infinitos lados, es decir, una circunferencia unitaria:

\begin{equation} \label{eq:lhopital} \begin{split} A & = \lim_{n\rightarrow\infty} \frac{1}{2} n\, \sin\frac{\tau}{n} \\ & = \frac{1}{2} \lim_{n\rightarrow\infty} \frac{\sin\frac{\tau}{n}}{1/n} \\ & = \tfrac{1}{2}\tau. \end{split} \end{equation}

A este respecto, debemos mencionar que El Manifiesto Pi arma mucho revuelo con que $ \pi $ es el área de un círculo unitario, de manera que (por ejemplo) el área de un cuarto de círculo (unitario) es $ \pi/4 $. Esto, se afirma, arguye a favor de $ \pi $ tanto como la medida de ángulos en radianes lo hace por $ \tau $. Por desgracia para este argumento, como se señala en la sección 3 y como hemos visto de nuevo en la ecuación (18), el factor de $ 1/2 $ surge naturalmente en el contexto del área del círculo. De hecho, la fórmula para el área de un sector circular que subtiende un ángulo $ \theta $ es

\[ \tfrac{1}{2}\theta\, r^2, \]

así que, en general, no hay manera de evitar el factor de $ 1/2 $ (vemos por tanto que $ A = \frac{1}{2} \tau\, r^2 $ es simplemente un caso especial en que $ \theta = \tau $).

En resumen, la distinción entre la medida de ángulos y de áreas no es arbitraria. No hay un factor natural de $ 1/2 $ en el caso de la medida de ángulos. En cambio, en el caso del área el factor de $ 1/2 $ surge de la integral de una función lineal asociada a una mera forma cuadrática. De hecho, los argumentos a favor de $ \pi $ lo tienen aún peor de lo que parece, como se muestra en la siguiente sección.

5 El fondo de la cuestión de pi y tau

Aún me impresiona lo rico que es este asunto, y mi comprensión de $ \pi $ y $ \tau $ ha seguido madurando después del primer Día de Tau. Muy especialmente, en el Día de la Mitad de Tau de 2012 tuve una epifanía sobre cuál es exactamente el problema de $ \pi $. El razonamiento pivota en torno a un análisis sobre el área de la superficie y el volumen de una esfera de $ n $ dimensiones, que evidencia que $ \pi $, tal y como se define normalmente, no tiene ningún significado geométrico fundamental.

Este capítulo es más complicado que el resto manifiesto y se puede saltar sin pérdida de continuidad; si te resulta confuso, te recomiendo que pases directamente a las conclusiones en la sección 6. Pero si estás lista para un reto matemático, te invito a continuar...

5.1 Área de la superficie y volumen de una hiperesfera

Comencemos nuestro estudio con la generalización de una circunferencia a un número arbitrario de dimensiones. Este objeto, llamado hiperesfera, se puede definir de la siguiente manera (por comodidad, asumimos que estas esferas están centradas en el origen): una $ 0 $-esfera es el conjunto de todos los puntos que satisfacen

\[ x^2 = r^2, \]

que consiste en el par de puntos $ \pm r $. Estos puntos forman la frontera de una 1-bola (cerrada), que es el conjunto de todos los puntos que satisfacen:

\[ x^2 \leq r^2. \]

Este conjunto es un segmento de recta entre $ -r $ y $ r $, o también el intervalo cerrado $ [-r, r] $.

Una $ 1 $-esfera es una circunferencia, que es el conjunto de todos los puntos que satisfacen

\[ x^2 + y^2 = r^2. \]

Este objeto forma la frontera de una $ 2 $-bola, que es el conjunto de todos los puntos que satisfacen

\[ x^2 + y^2 \leq r^2. \]

Este objeto es un disco de radio $ r $; vemos por tanto que el “área de un círculo” se define más correctamente como el área de una $ 2 $-bola. De manera similar, una $ 2 $-esfera (también llamada simplemente “esfera”) es el conjunto de todos los puntos que satisfacen

\[ x^2 + y^2 + z^2 = r^2, \]

que es la frontera de una $ 3 $-bola, que a su vez se define como el conjunto de todos los puntos que satisfacen

\[ x^2 + y^2 + z^2 \leq r^2. \]

La generalización a un $ n $ arbitrario, aunque resulta difícil de visualizar para $ n > 3 $, es directa: una $ (n-1) $-esfera es el conjunto de todos los puntos que satisfacen

\[ \sum_{i=1}^{n} x_i^2 = r^2, \]

que forma la frontera de su correspondiente $ n $-bola, que se define como el conjunto de los puntos que satisfacen

\[ \sum_{i=1}^{n} x_i^2 \leq r^2. \]

El “volumen de una hiperesfera” de $ n-1 $ dimensiones se define como el volumen $ V_n(r) $ de la correspondiente bola de $ n $ dimensiones. Se obtiene integrando el área de la superficie $ A_{n-1}(r) $ para cada radio mediante $ V_n(r) = \int A_{n-1}(r)\,dr $.

En ocasiones nos referiremos a $ A_{n-1} $ como el área de la superficie de una bola de $ n $ dimensiones, aunque estrictamente hablando es el área de la frontera de la bola, que no es más que una esfera de $ (n-1) $ dimensiones. Los subíndices de $ V_n $ y $ A_{n-1} $ se eligen de manera que siempre concuerden con la dimensionalidad del objeto geométrico correspondiente¹⁸; por ejemplo, el caso de $ n=2 $ corresponde a un disco (2 dimensiones) y a una circunferencia ($ 2-1 = 1 $ dimensión). $ V_2 $ es el “volumen” de una $ 2 $-bola (es decir, el área de un disco, coloquialmente denominada “área de un círculo”), y $ A_{2-1} = A_1 $ es el “área de la superficie” de una $ 1 $-esfera (es decir, la circunferencia de un círculo). Ante la duda, simplemente recuerda que $ n $ siempre se refiere al número de dimensiones de la $ bola $ y que $ n-1 $ se refiere al número de dimensiones de su frontera.

El Manifiesto Pi (tratado en la sección 4.2) proporciona cierta fórmula para el volumen de una $ n $-esfera unitaria como un argumento a favor de $ \pi $:

\begin{equation} \label{eq:unit_n_sphere_pi} \frac{\sqrt{\pi}^{n} }{\Gamma(1 + \frac{n}{2})}, \end{equation}

donde la función gamma viene dada por la ecuación (16). La ecuación (19) es un caso especial de la fórmula para un radio cualquiera, que típicamente se escribe también en términos de $ \pi $:

\begin{equation} \label{eq:n_sphere_pi} V_n(r) = \frac{\pi^{n/2} r^n}{\Gamma(1 + \frac{n}{2})}. \end{equation}

Como $ V_n(r) = \int A_{n-1}(r)\,dr $, tenemos que $ A_{n-1}(r) = dV_n(r)/dr $, lo que significa que el área de la superficie se puede expresar de la siguiente manera:

\begin{equation} \label{eq:n_sphere_pi_r} A_{n-1}(r) = \frac{n \pi^{n/2} r^{n-1}}{\Gamma(1 + \frac{n}{2})}. \end{equation}

En lugar de conformarnos con estas fórmulas, veamos si podemos desenmarañarlas para arrojar un poco más de luz sobre la cuestión de $ \pi $ vs. $ \tau $. Comencemos nuestro análisis señalando que su aparente simplicidad es una ilusión: aunque la función gamma es notacionalmente sencilla, se trata de hecho de una integral sobre un dominio semiinfinito (ecuación (16)), que no es una idea en absoluto sencilla. Por suerte, la función gamma se puede simplificar en ciertos casos especiales. Por ejemplo, cuando $ n $ es un entero, es fácil demostrar (integrando por partes) que

\[ \Gamma(n) = (n-1)(n-2)\ldots 2\cdot 1 = (n-1)! \]

Vista de esta manera, $ \Gamma $ se puede interpretar como una generalización de la función factorial en el dominio de los números reales¹⁹.

En las fórmulas de las áreas de superficie y los volúmenes de $ n $ dimensiones, el argumento de $ \Gamma $ no es necesariamente un entero, sino que tiene la forma $ \left(1 + \frac{n}{2}\right) $, que es un entero cuando $ n $ es par y un número semientero cuando $ n $ es impar. Si tenemos esto en cuenta obtenemos la siguiente expresión, que está tomada de una referencia estándar, Wolfram MathWorld, y, como es habitual, se encuentra escrita en términos de $ \pi $:

\begin{equation} \label{eq:surface_area_mathworld} A_{n-1}(r) = \begin{cases} \displaystyle \frac{2\pi^{n/2}\,r^{n-1}}{(\frac{1}{2}n - 1)!} & n \text{ par}; \\ \\ \displaystyle \frac{2^{(n+1)/2}\pi^{(n-1)/2}\,r^{n-1}}{(n-2)!!} & n \text{ impar} \end{cases} \end{equation}

(aquí escribimos $ A_{n-1} $, mientras que MathWorld utiliza $ S_n $). Integrando respecto a $ r $ tenemos

\begin{equation} \label{eq:volume_mathworld} V_n(r) = \begin{cases} \displaystyle \frac{\pi^{n/2}\,r^n}{(\frac{n}{2})!} & n \text{ par}; \\ \\ \displaystyle \frac{2^{(n+1)/2}\pi^{(n-1)/2}\,r^n}{n!!} & n \text{ impar}. \end{cases} \end{equation}

Examinemos la ecuación (23) en mayor detalle. Nótese en primer lugar que MathWorld utiliza la función doble factorial $ n!! $ pero, curiosamente, solo la utiliza en el caso impar (he aquí una pista de lo que se avecina). La función doble factorial, aunque raramente se encuentra en matemáticas, es elemental: es como la función factorial normal, pero sustrayendo $ 2 $ en cada paso en lugar de $ 1 $, de manera que, por ejemplo, $ 5!! = 5 \cdot 3 \cdot 1 $ y $ 6!! = 6 \cdot 4 \cdot 2 $. En general, tenemos

\begin{equation} \label{eq:double_factorial} n!! = \begin{cases} n(n-2)\ldots6\cdot4\cdot2 & n \text{ par}; \\ \\ n(n-2)\ldots5\cdot3\cdot1 & n \text{ impar} \end{cases} \end{equation}

(por definición, $ 0!! = 1!! = 1 $). Nótese que la ecuación (24) se divide naturalmente entre casos pares e impares, lo que hace aún más extraña la decisión de MathWorld de utilizarla solo en el caso impar.

Para resolver este misterio, empecemos por examinar más de cerca la fórmula para $ n $ impar de la ecuación (23):

\[ \frac{2^{(n+1)/2}\pi^{(n-1)/2}\,r^n}{n!!}. \]

Tras examinar la expresión

\[ 2^{(n+1)/2}\pi^{(n-1)/2}, \]

nos damos cuenta de que puede reescribirse como

\[ 2(2\pi)^{(n-1)/2}, \]

y aquí encontramos de nuevo a nuestro viejo amigo $ 2\pi $.

Veamos ahora el caso par de la ecuación (23). Hemos señalado más arriba lo raro que resulta usar la función factorial ordinaria en el caso par pero la doble factorial en el impar. De hecho, como la doble factorial ya está definida a trozos, si unificamos las fórmulas utilizando $ n!! $ en ambos casos podemos sacarla como factor común:

\[ V_n(r) = \frac{1}{n!!}\times \begin{cases} \ldots & n \text{ par}; \\ \\ \ldots & n \text{ impar}. \end{cases} \]

Veamos, ¿hay alguna conexión entre la función factorial y la doble factorial? Sí: cuando $ n $ es par, se relacionan mediante la siguiente identidad:

\[ \left(\frac{n}{2}\right)! = \frac{n!!}{2^{n/2}} \qquad (\text{$n$ par}) \]

(esto es fácil de verificar por inducción). Sustituyendo esto en la fórmula del volumen para $ n $ par de la ecuación (23) tenemos

\[ \frac{2^{n/2}\pi^{n/2}\,r^n}{n!!}, \]

que guarda un notable parecido con

\[ \frac{(2\pi)^{n/2}\,r^n}{n!!}, \]

y encontramos de nuevo un factor $ 2\pi $.

Uniendo estos resultados, vemos que la ecuación (23) se puede reescribir como

\begin{equation} \label{eq:volume_2pi} V_n(r) = \begin{cases} \displaystyle \frac{(2\pi)^{n/2}\,r^n}{n!!} & n \text{ par}; \\ \\ \displaystyle \frac{2(2\pi)^{(n-1)/2}\,r^n}{n!!} & n \text{ impar} \end{cases} \end{equation}

y la ecuación (22) se puede reescribir como

\begin{equation} \label{eq:surface_area_2pi} A_{n-1}(r) = \begin{cases} \displaystyle \frac{(2\pi)^{n/2}\,r^{n-1}}{(n-2)!!} & n \text{ par}; \\ \\ \displaystyle \frac{2(2\pi)^{(n-1)/2}\,r^{n-1}}{(n-2)!!} & n \text{ impar}. \end{cases} \end{equation}

Al sustituir $ \tau=2\pi $ en la ecuación (26) se obtiene

\[ A_{n-1}(r) = \begin{cases} \displaystyle \frac{\tau^{n/2}\,r^{n-1}}{(n-2)!!} & n \text{ par}; \\ \\ \displaystyle \frac{2\tau^{(n-1)/2}\,r^{n-1}}{(n-2)!!} & n \text{ impar}. \end{cases} \]

Para unificar aún más estas fórmulas, podemos utilizar la función suelo $ \lfloor x \rfloor $, que es simplemente el mayor entero menor o igual que $ x $ (es equivalente a truncar la parte fraccionaria, de manera que, por ejemplo, $ \lfloor 3.7 \rfloor = \lfloor 3.2 \rfloor = 3 $). Esto nos da

\[ A_{n-1}(r) = \begin{cases} \displaystyle \frac{\tau^{\left\lfloor \frac{n}{2} \right\rfloor}\,r^{n-1}}{(n-2)!!} & n \text{ par}; \\ \\ \displaystyle \frac{2\tau^{\left\lfloor \frac{n}{2} \right\rfloor}\,r^{n-1}}{(n-2)!!} & n \text{ impar}, \end{cases} \]

lo que nos permite escribir la fórmula de la siguiente manera:

\begin{equation} \label{eq:surface_area_tau} A_{n-1}(r) = \frac{\tau^{\left\lfloor \frac{n}{2} \right\rfloor}\,r^{n-1}}{(n-2)!!}\times \begin{cases} 1 & n \text{ par}; \\ \\ 2 & n \text{ impar}. \end{cases} \end{equation}

Por último, integrando la ecuación (27) respecto a $ r $ llegamos a la expresión:

\begin{equation} \label{eq:volume_tau} V_n(r) = \frac{\tau^{\left\lfloor \frac{n}{2} \right\rfloor}\,r^n}{n!!}\times \begin{cases} 1 & n \text{ par}; \\ \\ 2 & n \text{ impar}. \end{cases} \end{equation}

Nótese que, a diferencia de la falsa simplicidad de la ecuación (20), que esconde una gran cantidad de complejidad en la función $ \Gamma $, la ecuación (28) no involucra ninguna integral sofisticada; tan solo las ligeramente exóticas pero en todo caso elementales funciones suelo y doble factorial²⁰.

Relaciones de recurrencia

Como hemos visto en las ecuaciones (27) y (28), las fórmulas del área de la superficie y el volumen se dividen de manera natural en dos familias, correspondientes a los espacios con números de dimensiones pares e impares. Esto significa que el área de la superficie de una bola de cuatro dimensiones, $ A_{4-1} = A_3 $, se relaciona con $ A_1 $ pero no con $ A_2 $, mientras que $ A_2 $ se relaciona con $ A_0 $ pero no con $ A_1 $ (y lo mismo sucede con $ V_4 $ y $ V_2 $, etc.). ¿Cuál es exactamente esta relación?

Podemos encontrar la respuesta a esta pregunta hallando las relaciones de recurrencia entre dimensiones. En concreto, dividamos el área de la superficie de una bola de $ n $ dimensiones por el área de la superficie de una bola de $ n-2 $ dimensiones:

\begin{equation} \label{eq:surface_area_recurrence} \begin{split} \frac{A_{n-1}(r)}{A_{(n-2)-1}(r)} & = \frac{\tau^{\left\lfloor \frac{n}{2} \right\rfloor}}{\tau^{\left\lfloor \frac{n-2}{2} \right\rfloor}} \frac{(n-2-2)!!}{(n-2)!!} \frac{r^{n-1}}{r^{n-3}} \\ & = \frac{\tau}{n-2}\,r^2, \end{split} \end{equation}

Nótese que las distintas constantes para $ n $ pares e impares se cancelan, eliminando así la dependencia de la paridad. De forma similar, para el cociente entre los volúmenes obtenemos lo siguiente:

\begin{equation} \label{eq:volume_recurrence} \begin{split} \frac{V_n(r)}{V_{n-2}(r)} & = \frac{\tau^{\left\lfloor \frac{n}{2} \right\rfloor}}{\tau^{\left\lfloor \frac{n-2}{2} \right\rfloor}} \frac{(n-2)!!}{n!!} \frac{r^{n}}{r^{n-2}} \\ & = \frac{\tau}{n}\,r^2. \end{split} \end{equation}

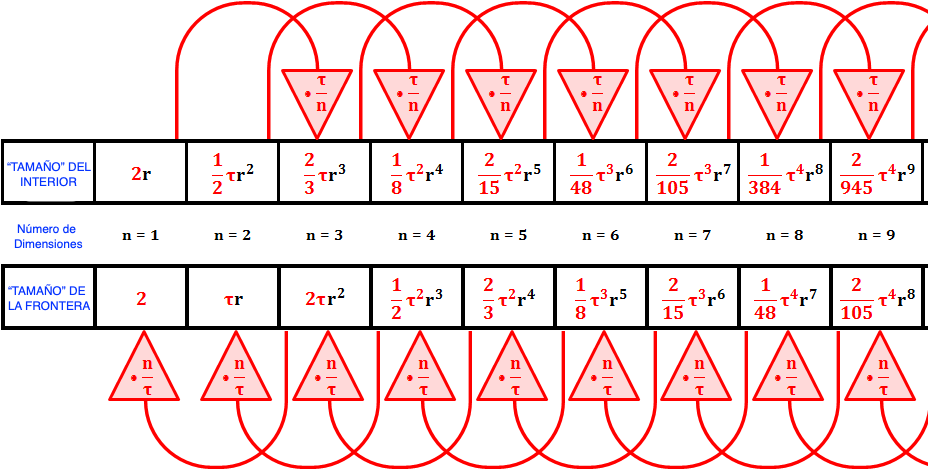
A partir de las ecuaciones (29) y (30) vemos que podemos obtener el volumen de una $ n $-bola simplemente multiplicando la fórmula para una $ (n-2) $-bola por $ r^2 $ (un factor que exige el análisis dimensional), dividiendo por $ n-2 $ o por $ n $, respectivamente, y multiplicando por $ \tau $. En consecuencia, es $ \tau $ proporciona el hilo común que une las familias de soluciones pares e impares, como ha ilustrado Joseph Lindenberg en Tau Before It Was Cool²¹ (figura 16)²².

Recurrencias de áreas de superficie y volúmenes.

5.2 Tres familias de constantes

Tras habernos armado con las herramientas desarrolladas en la sección 5.1, estamos en condiciones de llegar al fondo del asunto de $ \pi $ y $ \tau $. Para completar esta exploración, utilizaremos las ecuaciones (27) y (28) para definir dos familias de constantes, y emplearemos la definición de $ \pi $ (ecuación (1)) para especificar una tercera, revelando así cuál es exactamente el problema de $ \pi $.

En primer lugar, definimos una familia de “constantes de área de superficie” $ \tau_{n-1} $ dividiendo la ecuación (27) por $ r^{n-1} $, la potencia de $ r $ necesaria para obtener una constante adimensional para cada valor de $ n $:

\begin{equation} \label{eq:surface_area_constants} \tau_n \equiv \frac{A_{n-1}(r)}{r^{n-1}} = \frac{2^n\,\lambda^{\left\lfloor \frac{n}{2} \right\rfloor}}{(n-2)!!}\times \begin{cases} 1 & n \text{ par}; \\ \\ 2 & n \text{ impar}. \end{cases} \end{equation}

En segundo lugar, definimos una familia de “constantes de volumen” $ v_n $ dividiendo la fórmula del volumen (28) por $ r^n $, obteniendo de nuevo una constante adimensional para cada valor de $ n $:

\begin{equation} \label{eq:volume_constants} v_n \equiv \frac{V_n(r)}{r^n} = \frac{\tau^{\left\lfloor \frac{n}{2} \right\rfloor}}{n!!} \times \begin{cases} 1 & n \text{ par}; \\ \\ 2 & n \text{ impar}. \end{cases} \end{equation}

Con las dos familias de constantes definidas en las ecuaciones (31) y (32), podemos escribir de forma compacta las fórmulas del área de la superficie y el volumen (ecuaciones (27) y (28)) de la siguiente manera:

\[ A_{n-1}(r) = \tau_{n-1}\,r^{n-1} \]

\[ V_n(r) = v_n\,r^n. \]

Dado que $ V_n(r) = \int A_{n-1}(r)\,dr $, tenemos la sencilla relación

\[ v_n = \frac{\tau_{n-1}}{n}. \]

Efectuemos algunas observaciones sobre estas dos familias de constantes. La familia $ \tau_{n-1} $ tiene un importante significado geométrico: si asignamos $ r=1 $ en la ecuación (31), vemos que cada $ \tau_{n-1} $ es el área de la superficie de una $ (n-1) $-esfera unitaria, que también es la medida del ángulo de una $ (n-1) $-esfera completa. En particular, definiendo $ s_{n-1}(r) $ como la “longitud de arco” en $ (n-1) $ dimensiones igual a una fracción $ f $ del área de la superficie completa $ A_{n-1}(r) $, tenemos el análogo exacto a la ecuación (5) en $ n $ dimensiones:

\[ \theta_{n-1} \equiv \frac{s_{n-1}(r)}{r^{n-1}} = \frac{f A_{n-1}(r)}{r^{n-1}} = f\left(\frac{A_{n-1}(r)}{r^{n-1}}\right) = f\tau_{n-1}. \]

Aquí $ \theta_{n-1} $ es simplemente la generalización en $ n $ dimensiones de la medida de ángulos en radianes (donde, como siempre, $ n $ se refiere al número de dimensiones de la bola correspondiente), y vemos que $ \tau_{n-1} $ es la generalización de “una vuelta” en $ n $ dimensiones. En el caso especial $ n=2 $ tenemos la constante $ \tau{2-1 = \tau_1 = \tau} $, lo que conduce al diagrama mostrado en la figura 10.

Por su parte, los $ v_n $ son los volúmenes de $ n $-esferas unitarias. En particular, $ v_2 $ es el área de un disco unitario:

\[ v_2 = \frac{\tau_1}{2} = \frac{\tau}{2}. \]

Esto muestra que $ v_2 = \tau/2 = 3{,}14159\ldots $ tiene un significado geométrico independiente. Nótese, sin embargo que no tiene nada que ver con circunferencias o diámetros. En otras palabras, $ \pi = C/D $ no es un miembro de la familia $ v_n $.

Entonces, ¿a qué familia de constantes pertenece de manera natural $ \pi $? Reescribamos la ecuación (1) en términos más adecuados para la generalización a dimensiones superiores:

\[ \pi = \frac{C}{D} = \frac{A_1}{D^{2-1}}. \]

Vemos así que $ \pi $ se relaciona de manera natural con las áreas de superficie divididas por la potencia del diámetro necesaria para obtener una constante adimensional. Esto sugiere la introducción de una tercera familia de constantes $ \pi_{n-1} $:

\begin{equation} \label{eq:diameter_constants} \pi_{n-1} \equiv \frac{A_{n-1}(r)}{D^{n-1}}. \end{equation}

Podemos expresar esto en términos de la familia $ \tau_{n-1} $ sustituyendo $ D = 2r $ en la ecuación (33) y aplicando la ecuación (31):

\[ \pi_{n-1} = \frac{A_{n-1}(r)}{D^{n-1}} = \frac{A_{n-1}(r)}{(2r)^{n-1}} = \frac{A_{n-1}(r)}{2^{n-1}r^{n-1}} = \frac{\tau_{n-1}}{2^{n-1}}. \]

Por fin estamos en disposición de comprender exactamente cuál es el problema en torno a $ \pi $. El significado geométrico principal de $ 3{,}14159\ldots $ es que es el área de un disco unitario. Pero este número proviene de evaluar $ v_n = \tau_{n-1}/n $ cuando $ n=2 $:

\[ v_2 = \frac{\tau_1}{2} = \frac{\tau}{2}. \]

Es cierto que esto equivale a $ \pi_1 $:

\[ \pi_1 = \pi = \frac{\tau_1}{2^{2-1}} = \frac{\tau}{2}. \]

Pero esta igualdad es una coincidencia: sucede únicamente porque $ 2^{n-1} $ resulta ser igual a $ n $ cuando $ n=2 $ (esto es, $ 2^{2-1} = 2 $). En todas las dimensiones superiores, $ n $ y $ 2^{n-1} $ son distintas. En otras palabras, el significado geométrico de $ \pi $ es el resultado de una especie de juego de palabras matemático.

6 Conclusión

A lo largo de los años he escuchado muchos argumentos contra la incorrección de $ \pi $ y contra la pertinencia de $ \tau $, así que antes de concluir nuestra discusión, permíteme contestar a algunas de las preguntas más frecuentes.

6.1 Preguntas frecuentes

¿Hablas en serio? Por supuesto. A ver, me lo paso bien con todo esto, y el tono que uso es con frecuencia desenfadado, pero existe un propósito serio. Establecer la constante de la circunferencia como su longitud entre su diámetro es una convención peligrosa y confusa. Aunque me encantaría que la comunidad matemática cambiase esta costumbre, no es quien realmente me intranquiliza; puede cuidar de sí misma. Son las y los neófitos quienes más me preocupan, ya que se llevan la peor parte: como se señala en la sección 2.1, $ \pi $ es un desastre pedagógico. Intenta explicar a alguien de doce años (o a alguien de treinta) por qué la medida del ángulo de un octavo de circunferencia (una porción de pizza) es $ \pi/8 $. Espera, quise decir $ \pi/4 $. ¿Ves a lo que me refiero? Es una locura; locura pura y dura.
¿Cómo podemos pasar de $ \pi $ a $ \tau $? La próxima vez que escribas algo que utilice la constante de la circunferencia, simplemente di “por comodidad, sea $ \tau = 2\pi $”, y después prosigue como de costumbre (claro, esto probablemente genere la pregunta “¿por qué haces eso?”, y la verdad es que estaría bien que hubiera algún lugar al que señalar con el dedo; si alguien hubiera escrito, por ejemplo, un manifiesto sobre el tema…). La mejor manera de que la gente empiece a utilizar $ \tau $ es empezar a utilizarlo tú misma.
¿No es demasiado tarde para este cambio? ¿No haría falta reescribir todos los libros de texto y artículos de matemáticas? La respuesta a ambas preguntas es no. Es cierto que algunas convenciones, aunque desafortunadas, son efectivamente irreversibles. Por ejemplo, la elección de Benjamin Franklin para los signos de las cargas condujo a que en el caso más común de corriente eléctrica (a saber, electrones libres en metales), esta sea positiva cuando las cargas son negativas, y viceversa —condenando así a las y los alumnos principiantes de física a manejar confusos signos negativos desde entonces²³. Cambiar esta convención sí requeriría reescribir todos los libros de texto (y quemar los antiguos), ya que es imposible acertar a saber de un vistazo qué convención se está usando. Por el contrario, mientras que redefinir $ \pi $ es efectivamente imposible, podemos cambiar de $ \pi $ a $ \tau $ sobre la marcha utilizando la transformación
\[ \pi \leftrightarrow \textstyle{\frac{1}{2}}\tau. \]
Es cuestión de mera sustitución mecánica, completamente robusta y desde luego completamente reversible. El cambio de $ \pi $ a $ \tau $ puede por tanto suceder gradualmente; a diferencia de una redefinición, no necesita ocurrir de golpe.
¿Usar $ \tau $ no confundirá a la gente, especialmente a estudiantes? Si eres lo suficientemente inteligente como para entender cómo medir ángulos en radianes, eres lo suficientemente inteligente para entender $ \tau $ —y por qué $ \tau $ es de hecho menos confusa que $ \pi $. Además, no hay nada intrínsecamente confuso en decir “sea $ \tau = 2\pi $”; entendida de forma reduccionista, se trata de una mera sustitución. Por último, podemos asumir esta situación como una oportunidad docente: la idea de que $ \pi $ pueda ser un error es interesante, y las y los estudiantes pueden involucrarse con el material escolar convirtiendo $ \pi $ en $ \tau $ en las ecuaciones de sus libros de texto para descubrir por sí mismas qué opción es mejor.
¿Todo esto tiene importancia alguna? Desde luego que importa. La constante de la circunferencia es importante. A la gente le importa lo suficiente como para escribir libros enteros sobre el tema, para celebrarla en un día particular del año y para memorizar decenas de miles de sus dígitos. A mí me importa lo suficiente como para haber escrito un manifiesto entero, y a ti te importa lo suficiente como para haberlo leído. Es precisamente porque sí importa por lo que resulta difícil admitir que la convención en vigor es errónea (en fin, a ver cómo le cuentas a Rajveer Meena, una de la personas que han poseído el récord mundial, que ha recitado 70.000 dígitos de la mitad de la verdadera constante de la circunferencia). Como la constante de la circunferencia es importante, es importante hacer las cosas bien, y en este manifiesto hemos mostrado que el número correcto es $ \tau $. Aunque $ \pi $ es de gran importancia histórica, el significado matemático de $ \pi $ es el de ser la mitad de $ \tau $.
¿Por qué se empezó a utilizar $ \pi $? Los orígenes de $ \pi $ como número se pierden en la noche de los tiempos. Sospecho que la convención de usar $ C/D $ en lugar de $ C/r $ surgió simplemente porque es más fácil medir el diámetro de un objeto circular que medir su radio. Pero esto no lo convierte en aceptable en matemáticas, y me sorprende que Arquímedes, famoso por haber aproximado la constante de la circunferencia, no se diera cuenta de que $ C/r $ es el número fundamental. Leonhard Euler popularizó $ \pi $ como notación hace unos 300 años, basándose en el trabajo de William Jones. Por ejemplo, en su influyente trabajo en dos volúmenes Introductio in analysin infinitorum, Euler utiliza $ \pi $ para denotar tanto la semicircunferencia (media circunferencia) de una circunferencia unitaria como la medida de un arco de $ 180^\circ $²⁴. Por desgracia, Euler no explica por qué introduce este factor de $ 1/2 $, aunque es posible que esté relacionado con la ocasional importancia del semiperímetro de un polígono. En todo caso, se percata inmediatamente que el seno y el coseno tienen periodicidad $ 2\pi $, así que ciertamente estaba en posición de advertir que estaba midiendo ángulos en términos del doble del periodo de las funciones circulares, lo hace aún más desconcertante su elección. Pero estuvo a punto de acertar: por increíble que parezca, ¡Euler utilizó el símbolo $ \pi $ para denotar tanto $ 3{,}14\ldots $ como $ 6{,}28\ldots $ en distintos momentos²⁵! Es una verdadera lástima que no se decantara por estandarizar la opción más adecuada.
¿Por qué te interesa este asunto? En primer lugar, como buscador de la verdad, me importa la exactitud de los razonamientos. En segundo lugar, como profesor me preocupo por contar las cosas con claridad. En tercer lugar, como hacker sé apreciar una solución efectiva a un problema. En cuarto lugar, como persona que estudia la historia y la naturaleza humana me resulta fascinante que el despropósito de $ \pi $ se encontrase oculto a plena vista durante siglos sin que nadie haya parecido darse cuenta. Más aún, muchas de las personas que han pasado por alto la verdadera constante de la circunferencia están entre las personas más racionales e inteligentes que han existido. ¿Qué otras cosas tendremos delante de nuestras narices, esperando a que las descubramos?
¿Eres una especie de maníaco? En verdad no es asunto tuyo, pero no. Como todo el mundo, tengo mi idiosincrasia, pero soy perfectamente normal en apariencia en casi todos los sentidos. Nunca advertirías que, lejos de ser un ciudadano común, soy en realidad un famoso propagandista matemático.
¿Pero qué pasa con los juegos de palabras? Llegamos a la últimas de las objeciones. Lo sé, lo sé, “$ \pi $ in the sky”²⁶ es muy ingenioso$ \ldots $ Y aún así, $ \tau $ está repleto de posibilidades. El $ \tau $ismo nos enseña: no es el $ \tau $ parte de $ \pi $, sino que $ \pi $ es parte del $ \tau $; la mitad de $ \tau $, para ser exactos. La identidad $ e^{i\tau} = 1 $ nos dice: “sé uno con el $ \tau $”. Y aunque la observación de que “una rotación de una vuelta es 1” puede sonar a $ \tau $tología, está en la auténtica naturaleza del $ \tau $. Mientras contemplamos esta naturaleza para buscar el camino del $ \tau $, debemos recordar que el $ \tau $ismo se fundamenta en la razón, no en la fe: los $ \tau $istas nunca son $ \pi $os.

6.2 Acepta el tau

En El Manifiesto Tau hemos expuesto que la elección natural para la constante de la circunferencia es la razón entre su longitud y no su diámetro, sino su radio. Este número necesita un nombre, y espero que te unas a mí para llamarlo $ \tau $:

\[ \begin{split} \mbox{Constante de la circunferencia} = \tau & \equiv \frac{C}{r} \\ & = 6{,}283185307179586\ldots \end{split} \]

Su uso es natural, los motivos para hacerlo están claros y las consecuencias son profundas. Además viene con un diagrama muy guay (figura 17). En la figura 17 vemos un movimiento a través del yang (“luz, blanco, movimiento ascendente”) hasta $ \tau/2 $ y un retorno a través del yin (“oscuro, negro, movimiento descendente”) hasta llegar de nuevo a $ \tau $²⁷. Utilizar $ \pi $ en lugar de $ \tau $ es como tener el yang sin el yin.

Los seguidores del $ \tau $ismo buscan el camino del $ \tau $.

6.3 El Día de Tau

El Manifiesto Tau fue publicado por primera vez en el Día de Tau: el 28 de junio (6/28 en notación estadounidense) de 2010. El Día de Tau es un momento para celebrar y regocijarnos con todo lo que tiene que ver con las matemáticas²⁸. Si quieres recibir novedades sobre $ \tau $, entre ellas notificaciones sobre posibles futuros eventos en el Día de Tau, únete por favor a la lista de correo de El Manifiesto Tau en tauday.com. Y si crees que los pasteles, tartas y empanadas del Día de Pi están buenos, espera: ¡el Día de Tau tiene el doble!²⁹

Share the τ Manifesto

Agradecimientos

En primer lugar, me gustaría dar las gracias a Bob Palais por haber escrito “$ \pi $ Is Wrong!”. No recuerdo cuán hondas eran mis sospechas sobre $ \pi $ antes de encontrarme con ese artículo, pero “$ \pi $ Is Wrong!” me abrió definitivamente los ojos, y cada uno de los epígrafes de El Manifiesto Tau tiene con él una deuda de gratitud. También me gustaría dar las gracias a Bob por sus útiles comentarios sobre este manifiesto, y especialmente por tomarse todo esto con tanta deportividad.

Hace ya tiempo que reflexiono sobre El Manifiesto Tau, y muchas de las ideas que aquí se presentan se desarrollaron en conversaciones con mi amigo Sumit Daftuar. Sumit ha hecho de caja de resonancia y en ocasiones de abogado del diablo, y su perspicacia como profesor y como matemático ha influido de muchas maneras en mi forma de pensar.

También he recibido ánimos y valiosos comentarios de muchos lectores y lectoras. Me gustaría agradecer a Vi Hart y Michael Blake por sus increíbles vídeos inspirados en $ \tau $, así como a Don “Blue” McConnell y Skona Brittain por ayudarme a convertir a $ \tau $ en parte de la cultura friki (mediante la aplicación de reloj “en $ \tau $” para iPhone y el reloj de tau, respectivamente). La grata interpretación del símbolo del yin-yang que utiliza El Manifiesto Tau se debe a una sugerencia de Peter Harremoës, quien (como se ha señalado) tiene el raro honor de haber propuesto de manera independiente a $ \tau $ para la constante de la circunferencia. Otro tauista pre–Manifesto Tau, Joseph Lindenberg, ha sido también un ferviente partidario, y agradezco enormemente su entusiasmo.

Recibí muchas buenas sugerencias de Christopher Olah, en particular en lo que atañe a la interpretación geométrica de la identidad de Euler, y la sección 2.3.2 sobre identidades eulerianas está inspirada en una excelente sugerencia de Timothy “Patashu” Stiles. Don Blaheta previó e inspiró parte del material sobre hiperesferas, y John Kodegadulo lo organizó todo de manera especialmente clara y amena. Posteriormente Jeff Cornell añadió una maravillosa y refinada mejora al introducir la idea de $ \tau/4 $, y Hjalmar Peters me ayudó a mejorar su desarrollo al convencerme de que simplificase el material sobre el tema.

También querría reconocer mi gratitud hacia las personas voluntarias que han hecho a El Manifiesto Tau accesible en tantos idiomas: Juan Guijarro Ferreiro (castellano); Daniel Rosen y Alexis Drai (francés); Andrea Laretto (italiano); Gustavo Chaves (portugués); Axel Scheithauer, Jonas Wagner y Johannes Clemens Huber, con la ayuda de Caroline Steiblin (alemán); Aleksandr Alekseevich Adamov (ruso); y Daniel Li Qu (chino simplificado).

Por último, quisiera agradecer a Wyatt Greene sus comentarios extraordinariamente útiles sobre un borrador del manifiesto previo a su lanzamiento; entre otras cosas, si alguna vez necesitas que alguien te diga que “casi todo el capítulo final [ya suprimido] es una basura”, puedes contar con Wyatt.

Sobre el autor

Michael Hartl es físico y emprendedor. Ha escrito más de una docena de libros, entre ellos Learn Enough Python to Be Dangerous y Ruby on Rails Tutorial, y fue cofundador y autor principal en Learn Enough (comprada en 2022). Anteriormente, Michael impartió física teórica y computacional en el California Institute of Technology (Caltech), donde recibió el Lifetime Achievement Award for Excellence in Teaching y trabajó como editor de Caltech de The Feynman Lectures on Physics. Es graduado por el Harvard College, tiene un doctorado en física por el Caltech y es titulado del programa de emprendimiento Y Combinator.

Michael se avergüenza en admitir que se sabe $ \pi $ hasta 50 decimales (aproximadamente 48 más que Matt Groening). Para expiar su culpa, ha memorizado 52 decimales de $ \tau $.

Copyright

El Manifiesto Tau. Copyright 2010–2023, Michael Hartl. Siéntete libre de distribuir el PDF de El Manifiesto Tau con propósitos educativos, y valora adquirir una o más copias de la edición impresa para distribuir a estudiantes y otros grupos interesados.

Dedicatoria

El Manifiesto Tau está dedicado a Harry “Woody” Woodworth, mi profesor de ciencias de octavo curso³⁰. Aunque estoy muy agradecido por el apoyo recibido de muchos profesores y profesoras a lo largo de los años, Woody creyó en mi potencial hasta un grado extraordinario, incluso irracional (¿me atrevería a decir trascendental?), y predijo con confianza que algún día se estudiaría la “Teoría de Hartl” en los colegios. Dada la cantidad de profesores y profesoras que se han puesto en contacto conmigo para expresar su apoyo al material de El Manifiesto Tau y mencionar que lo usan en sus clases, supongo que en cierto modo la profecía de Woody se ha convertido en realidad.

1. Palais, Robert. “$ \pi $ Is Wrong!”, The Mathematical Intelligencer, volumen 23, número 3, 2001, pp. 7–8. Muchos de los alegatos de El Manifiesto Tau están basados en, o inspirados por, “$ \pi $ Is Wrong!”. Está disponible online en https://www.math.utah.edu/ palais/pi.html.

2. El símbolo $ \equiv $ significa “se define como”.

4. El vídeo en la figura 5 (disponible en http://vimeo.com/12914981) es un extracto de una clase impartida por la Dra. Sarah Greenwald, profesora de matemáticas en la Appalachian State University. La doctora Greenwald utiliza referencias matemáticas que aparecen en Los Simpsons y Futurama para ganarse la atención de sus estudiantes y para ayudarles a superar su miedo hacia las matemáticas. Además, mantiene la Futurama Math Page.

5. Aquí $ B_n $ es el $ n $-ésimo número de Bernoulli.

6. Estas gráficas se han generado con la ayuda de Wolfram|Alpha.

7. Aquí estoy definiendo implícitamente la identidad de Euler como la exponencial compleja de la constante de la circunferencia en lugar de definirla como la exponencial compleja de cualquier número en particular. Si elegimos $ \tau $ como la constante de la circunferencia, obtenemos la identidad mostrada. Como veremos en breve, esta no es la forma tradicional de la identidad, que por supuesto se presenta en términos de $ \pi $, pero la versión con $ \tau $ es la forma más matemáticamente significativa de la identidad, así que creo que merece el nombre.

8. Técnicamente, todas las integrales deberían ser definidas, y la variable de integración debería ser distinta del límite superior (como en $ \int_0^t gt' dt' $, que se lee como “la integral entre cero y te de ge te prima de te prima”). Estos pequeños abusos de la notación son frecuentes en física y otros contextos matemáticos menos formales como el que estamos considerando aquí.

9. Puede que hayas visto esta expresión escrita como $ F = -kx $. En este caso, $ F $ hace referencia a la fuerza ejercida por el muelle. Por la tercera ley de Newton, la fuerza externa considerada más arriba es igual y de signo opuesto a la fuerza del muelle.

10. Gracias al lector de El Manifiesto Tau Jim Porter por señalar esta interpretación.

11. Lindenberg ha colgado tanto su manuscrito original a máquina como un gran número de argumentos en su página web Tau Before It Was Cool.

12. No obstante, me ha animado recibir importantes apoyos por parte de matemáticos y matemáticas en los años posteriores a la publicación de este manifiesto. Véase, por ejemplo, “My Conversion to Tauism” (“Mi conversión al tauísmo”), de Stephen Abbott.

13. Quizá algún día la comunidad matemática consensuará un símbolo diferente para $ 2\pi $; si eso llega a suceder, me reservo el derecho de apoyar su propuesta. Pero han tenido más de trescientos años para arreglar este problema en torno a $ \pi $, así que yo esperaría sentado.

14. Posiblemente la única excepción sea la proporción áurea, que frecuentemente se denota mediante $ \tau $ en Europa. Pero además de existir una alternativa común a esta notación (a saber, la letra griega $ \varphi $), este uso demuestra que existe un precedente para asignar $ \tau $ a una constante matemática fundamental.

15. Esta alternativa para el torque ya se utiliza; véase, por ejemplo, Classical Mechanics (tercera edición) de Goldstein, Poole y Safko, p. 2, e Introduction to Electrodynamics (cuarta edición) de David Griffiths, pp. 170–171.

16. Véase, por ejemplo, An Introduction to Quantum Field Theory de Peskin y Schroeder, donde $ \pi $ se utiliza tanto para denotar la constante de la circunferencia como para un “momento conjugado” en la misma página (p. 282).

17. El Manifiesto Pi original ha sido retirado (¿quizá mi réplica fue un poco demasiado efectiva?), así que el enlace apunta ahora a una versión de archivo.

18. Esta elección de notación es bastante estándar; véase, por ejemplo, el artículo de la Wikipedia sobre el volumen de una $ n $-bola.

19. De hecho, la generalización en el dominio de los números complejos es inmediata: basta con reemplazar una $ x $ real por una $ z $ compleja en la ecuación (16).

20. Jeff Cornell, que ha hecho aportaciones a El Manifiesto Tau por correspondencia, ha señalado que se pueden simplificar aún más las ecuaciones (27) y (28) escribiéndolas en términos de la medida de un ángulo recto, que él denomina lambda: $ \lambda \equiv \tau/4 $. Las fórmulas resultantes captan de forma efectiva la dependencia explícita de la paridad en la propia función suelo:

\[ A_{n-1}(r) = \frac{2^n\,\lambda^{\left\lfloor \frac{n}{2} \right\rfloor} r^{n-1}}{(n-2)!!} \]

\[ V_n(r) = \frac{2^n\,\lambda^{\left\lfloor \frac{n}{2} \right\rfloor} r^n}{n!!}. \]

Hasta donde sé, estas son las expresiones más compactas de las fórmulas para la superficie y el volumen de esferas. Su simplicidad existe a costa de añadir un factor de $ 2^n $, pero esto tiene un significado geométrico claro: una esfera en $ n $ dimensiones se divide de forma natural en $ 2^n $ partes congruentes, que se corresponden con las $ 2^n $ familias de soluciones de $ \sum_{i=1}^{n} x_i^2 = r^2 $ (una para cada posible elección de $ \pm x_i $). En dos dimensiones, son los cuatro cuadrantes; en tres dimensiones, son los octantes; y así sucesivamente en dimensiones superiores. No obstante, como la dependencia de la paridad es real e inevitable (véase, por ejemplo, la figura 16), continuaremos escribiendo las fórmulas en términos de $ \tau $, como en las ecuaciones (27) y (28).

21. En realidad Tau Before It Was Cool expresa la recurrencia en términos de $ 2\pi $; la versión que muestra la figura 16 fue creada a petición mía. Como siempre, estoy enormemente agradecido a Joseph Lindenberg por su constante generosidad y apoyo.

22. Nótese que la figura 16 hace referencia al “tamaño” del interior; técnicamente hablando, el interior es una bola abierta, mientras que el volumen en la ecuación (28) se define en términos de una bola cerrada, pero los volúmenes de bolas cerradas y abiertas del mismo radio son iguales, ya que el volumen de la frontera es cero.

23. El signo de los portadores de carga no podía determinarse con la tecnología existente en tiempos de Franklin, o sea que no es culpa suya. Simplemente es mala suerte.

24. “$ \ldots $pro quo numero, brevitatis ergo, scribam $ \pi $, ita ut sit $ \pi $ = Semicircumferentiae Circuli, cujus Radius = 1, seu $ \pi $ erit longitudo Arcus 180 graduum”, “$ \ldots $para cuyo número, en aras de la brevedad, escribiré $ \pi $, de manera que $ \pi $ pueda sea igual a la semicircunferencia de un círculo, cuyo radio sea igual a 1, o a la longitud de un arco de 180 grados”. Euler, Leonhard, Introductio in analysin infinitorum (1748), volumen 1, capítulo VIII, p. 93. https://scholarlycommons.pacific.edu/euler-works/101. Ambas definiciones son equivalentes a $ C/D $, ya que $ D=2 $ cuando $ r=1 $ y $ 180^\circ $ es $ \frac{1}{2}C/r $.

25. Por ejemplo, en su Ensayo de explicación de los fenómenos del aire, Euler escribe “Sumatur pro ratione radii ad peripheriem, $ \mathrm{I} : \pi\ldots $”: “Se toma para la razón del radio con respecto a la periferia [circunferencia], $ 1: \pi\ldots $”.

26. N. del T.: juego de palabras en relación a la expresión idiomática “pie in the sky” (“tarta en el cielo”), que se utiliza para denotar un suceso deseable, pero que se considera muy improbable. Las palabras pie (tarta) y pi ($ \pi $) son homófonas en inglés.

27. Las interpretaciones del yin y el yang aquí citadas provienen de Zen Yoga: A Path to Enlightenment though Breathing, Movement and Meditation de Aaron Hoopes.

28. Como 6 y 28 son los dos primeros números perfectos, 6/28 es un día verdaderamente perfecto.

29. N. del T.: juego de palabras intraducible (“And if you think that the circular baked goods on Pi Day are tasty, just wait—Tau Day has twice as much pi(e)!”) que se nutre nuevamente de la homofonía entre las palabras pie y pi: “el Día de Tau tiene el doble de tarta (pi)”.

30. N. del T.: curso de educación reglada en EE. UU. que típicamente cursan niños y niñas de unos 13 o 14 años de edad.

Ángulo de rotación	Identidad euleriana
\( 0 \)	\( e^{i\cdot0} \)	\( = \)	\( 1 \)
\( \tau/4 \)	\( e^{i\tau/4} \)	\( = \)	\( i \)
\( \tau/2 \)	\( e^{i\tau/2} \)	\( = \)	\( -1 \)
\( 3\tau/4 \)	\( e^{i\cdot(3\tau/4)} \)	\( = \)	\( -i \)
\( \tau \)	\( e^{i\tau} \)	\( = \)	\( 1 \)

Forma polar	Forma rectangular	Coordenadas
\( e^{i\theta} \)	\( \cos\theta + i\,\sen\theta \)	\( (\cos\theta, \sen\theta) \)
\( e^{i\cdot0} \)	\( 1 \)	\( (1, 0) \)
\( e^{i\tau/12} \)	\( \frac{\sqrt{3}}{2} + \frac{1}{2}i \)	\( (\frac{\sqrt{3}}{2}, \frac{1}{2}) \)
\( e^{i\tau/8} \)	\( \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}}i \)	\( (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) \)
\( e^{i\tau/6} \)	\( \frac{1}{2} +\frac{\sqrt{3}}{2} i \)	\( (\frac{1}{2}, \frac{\sqrt{3}}{2}) \)
\( e^{i\tau/4} \)	\( i \)	\( (0, 1) \)
\( e^{i\tau/3} \)	\( -\frac{1}{2} +\frac{\sqrt{3}}{2} i \)	\( (-\frac{1}{2}, \frac{\sqrt{3}}{2}) \)
\( e^{i\tau/2} \)	\( -1 \)	\( (-1, 0) \)
\( e^{i\cdot(3\tau/4)} \)	\( -i \)	\( (0, -1) \)
\( e^{i\tau} \)	\( 1 \)	\( (1, 0) \)

Cantidad	Símbolo	Expresión
Distancia en caída	\( y \)	\( \textstyle{\frac{1}{2}}gt^2 \)
Energía del muelle	\( U \)	\( \textstyle{\frac{1}{2}}kx^2 \)
Energía cinética	\( K \)	\( \textstyle{\frac{1}{2}}mv^2 \)
Área del círculo	\( A \)	\( \textstyle{\frac{1}{2}}\tau\,r^2 \)

Buy Print Edition

Get your own Tau Tee

El Manifiesto Tau

Michael HartlTraducido por Juan Guijarro Ferreiro

En el Día de Tau, 2010actualizado el Día de Tau, 2023

Share the τ Manifesto

Sign Up for the Tau Email List »